Explicação da proporcionalidade composta, regra de três compostos, exercícios

O Composta ou múltipla proporcionalidade É a relação entre mais de duas magnitudes, onde a proporcionalidade direta e inversa pode ser observada entre os dados e o desconhecido. É uma versão mais avançada da proporcionalidade simples, embora as técnicas usadas em ambos os procedimentos sejam semelhantes.

Por exemplo, se 7 pessoas forem necessárias para baixar 10 toneladas de mercadorias em 3 horas, a proporcionalidade composta pode ser usada para calcular quantas pessoas serão necessárias para baixar 15 toneladas em 4 horas.

Fonte: Pixabay.com

Para responder a essa pergunta, é conveniente fazer uma tabela de valores para estudar e relacionar as magnitudes e incógnitas.

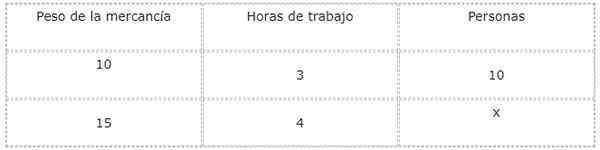
Os tipos de relações entre cada magnitude e o presente desconhecido são analisados, que neste caso corresponde ao número de pessoas que trabalharão.

À medida que o peso da mercadoria aumenta, o número de pessoas necessárias para baixar também aumenta. Por causa disso, a relação entre peso e trabalhadores é direta.

Por outro lado, aumentando o número de trabalhadores, o horário de trabalho diminui. Por causa disso, a relação entre as pessoas e o horário de trabalho é inversa.

[TOC]

Como calcular proporcionalidades compostas

Para resolver exemplos como o anterior, o método de regra com três compostos é usado principalmente. Isso consiste em estabelecer os tipos de relações entre magnitudes e incógnitas e depois representar um produto entre frações.

Com relação ao exemplo inicial, as frações correspondentes à tabela de valores são organizadas da seguinte forma:

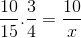
Mas antes de resolver e limpar o desconhecido, as frações correspondentes ao relacionamento inverso devem ser revertidas. Para este caso corresponder à variável de tempo. Dessa forma, a operação a ser resolvida será:

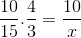
Cuja única diferença é o investimento da fração correspondente ao tempo variável 4/3. O valor de x é operado e claro.

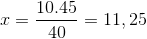
Assim, mais de onze pessoas são necessárias para baixar 15 toneladas de mercadorias em 4 horas ou menos.

Explicação

Proporcionalidade é a relação constante entre magnitudes que estão sujeitas a mudanças, o que será simétrico para cada uma das magnitudes envolvidas. Existem relacionamentos diretamente e inversamente proporcionais, definindo assim os parâmetros da proporcionalidade simples ou composta.

Regra direta de três

Consiste em uma proporção de proporção entre variáveis, que apresentam o mesmo comportamento quando modificado. É muito frequente no cálculo de porcentagens relacionadas a diferentes magnitudes de cem, onde sua estrutura fundamental é apreciada.

Como exemplo, você pode calcular 15% de 63. À primeira vista, a referida porcentagem não pode ser vista de uma maneira simples. Mas implementando a regra de três, você pode fazer o seguinte relacionamento: se 100% for 63, então 15%, quanto será?

Pode servir a você: fator Teorema: Explicação, Exemplos, Exercícios

100%-63

15%-x

E a operação correspondente é:

(quinze% . 63) / 100% = 9,45

Onde os sinais percentuais são simplificados e o número 9,45 que representa 15% de 63 é alcançado.

Três regras inversas

Como o nome indica, neste caso, a relação entre as variáveis ​​é contrária. A relação inversa deve ser estabelecida antes de prosseguir para o cálculo. Seu procedimento é homólogo da regra direta, com exceção do investimento na fração a ser calculada.

Por exemplo, 3 pintores precisam de 5 horas para terminar uma parede. Quantas horas terminariam 4 pintores?

Nesse caso, o relacionamento é inverso, pois aumentando o número de pintores, o tempo de trabalho deve diminuir. O relacionamento é estabelecido;

3 pintores - 5 horas

4 pintores- x horas

Quando o relacionamento é inverso, a ordem de operação é revertida. Sendo esta a maneira correta;

(3 pintores) . (5 horas) / 4 pintores = 3,75 horas

O termo pintores é simplificado e o resultado é de 3,75 horas.

Doença

Para estar na presença de um composto ou proporcionalidade múltipla, é necessário encontrar os dois tipos de relação entre magnitudes e variáveis.

- DIRECT: a variável apresenta o mesmo comportamento que o desconhecido. Isto é, aumentando ou diminuindo um, o outro é alterado igualmente.

- Inverso: a variável apresenta um comportamento de antônimo ao do desconhecido. A fração que define essa variável na tabela de valores deve ser revertida, a fim de representar a relação inversamente proporcional entre variável e desconhecida.

Verificação de resultados

É muito comum confundir a ordem das magnitudes ao trabalhar com proporcionalidades compostas, diferentemente do que acontece nos cálculos de proporção usual, cuja natureza é principalmente direta e resolúvel por meio de uma regra simples de três.

Portanto, é importante examinar a ordem lógica dos resultados, verificando a coerência das figuras lançadas pela regra de três compostos.

No exemplo inicial, cometer esse erro implicaria a obtenção de 20 como resultado. Isto é, 20 pessoas para baixar 15 toneladas de mercadorias em 4 horas.

A simple vista no parece un resultado descabellado, pero resulta curioso un aumento de casi un 200% en el personal (de 7 a 20 personas) cuando el aumento de mercancía es de un 50%, e incluso con un mayor margen de tiempo para realizar o trabalho.

Pode servir a você: Equação Geral de Parábola (Exemplos e Exercícios)

Dessa maneira, a verificação lógica dos resultados representa uma etapa importante implementando a regra de três compostos.

Liberação

Embora de uma natureza mais básica em relação à formação matemática, a depuração representa um passo importante nos casos de proporcionalidade. Uma liberação errônea é suficiente para invalidar qualquer resultado obtido na ordem de três simples ou compostos.

História

A regra de três ficou conhecida no Ocidente através dos árabes, com publicações de vários autores. Entre eles Al-Jwarizmi e Al-Biruni.

Al-Biruni, graças ao seu conhecimento multicultural, teve acesso a vastas informações sobre essa prática em suas viagens à Índia, sendo responsável pela documentação mais extensa sobre a regra dos três.

Ele aumenta em sua investigação, que a Índia foi o primeiro lugar onde o uso das três regra foi feito comuns. O escritor garante que foi feito fluentemente em suas versões diretas, inversas e até compostas.

A data exata em que a regra três se tornou parte do conhecimento matemático da Índia ainda é desconhecido. No entanto, o documento mais antigo destinado a essa prática, o manuscrito de Bakhshali, foi descoberto em 1881. Está atualmente em Oxford.

Muitos historiadores da matemática garantem que este manuscrito data do início da era atual.

Exercícios resolvidos

Exercício 1

Uma companhia aérea deve mover 1535 pessoas. Sabe -se que, com três aviões, levaria 12 dias para levar para o último passageiro para o destino. Mais 450 pessoas chegaram à companhia aérea e 2 aviões são ordenados a colaborar com esta tarefa. Quantos dias a companhia aérea levará para o último passageiro para seu destino?

A relação entre o número de pessoas e os dias de trabalho é direta, porque quanto mais pessoas, mais dias serão obrigados a realizar este trabalho.

Por outro lado, a relação entre aviões e dias é inversamente proporcional. Ao aumentar a quantidade de aviões, os dias necessários diminuem para transferir para todos os passageiros.

A tabela de valores referentes a este caso é realizada.

Conforme detalhado no exemplo inicial, o numerador e o denominador devem ser investidos na fração correspondente à variável reversa em relação ao desconhecido. Deixando a operação da seguinte forma:

Pode atendê -lo: cálculo de abordagens usando diferenciais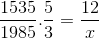

X = 71460/7675 = 9,31 dias

Para se mudar para 1985 pessoas usando 5 aviões, são necessários mais de 9 dias.

Exercício 2

Uma colheita de milho de 25 -T é levada para caminhões de carga. Sabe -se que no ano anterior levou 8 horas com uma folha de pagamento de 150 trabalhadores. Se para este ano a folha de pagamento aumentar 35%, quanto tempo levará para preencher os caminhões de carga com uma colheita de 40 -TON?

Antes de representar a tabela de valores, o número de trabalhadores para este ano deve ser definido. Isso aumentou 35% do número inicial de 150 trabalhadores. Para isso, uma regra direta é usada.

100% - 150

35% - x

X = (35 . 100)/100 = 52,5. Este é o número de trabalhadores adicionais em relação ao ano anterior, obtendo um número total de 203 trabalhadores, infelizes em arredondar o valor obtido.

A tabela de dados correspondente é definida

Para este caso, o peso representa uma variável de relacionamento direta com o tempo desconhecido. Por outro lado, a variável dos trabalhadores gerencia um relacionamento inverso com o tempo. Um número maior de trabalhadores, o dia será mais curto.

Levando essas considerações em consideração e investindo a fração correspondente aos trabalhadores, ela é calculada.

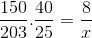
X = 40600 /6000 = 6,76 horas

O dia levará um pouco menos de 7 horas.

Exercícios propostos

- Defina 73% de 2875.

- Calcule a quantidade de horas em que Teresa dorme, se souber que apenas 7% do total do sono do dia. Defina quantas horas durma uma semana.

- Um jornal público de 2000 a cada 5 horas, usando apenas 2 máquinas impressas. Quantas cópias produzirão em 1 hora, se você usar 7 máquinas? Quanto tempo produzirá 10.000 cópias usando 4 máquinas?

Referências

1. Enciclopédia Alvarez-Iniciacion. PARA. Álvarez, Antonio Álvarez Pérez. Edaf, 2001.
2. Manual de instrução primária elementar e superior completa: para o uso de candidatos aos professores e especialmente aos alunos das escolas da província normal, volume 1. Joaquín Avendaño. Impressão d. Dionisio Hidalgo, 1844.
3. Aproximação de classificação de funções reais. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 de março. 2011.
4. Aritmética Elementar para Ensino em Escolas e Escolas na América Central. Darío González. Dica. Arenales, 1926.
5. O estudo da matemática: sobre o estudo e dificuldades da matemática. Augustus de Morgan. Baldwin e Cradock, 1830.