Matemática

Propriedades radicais

4422
300
Pete Wuckert

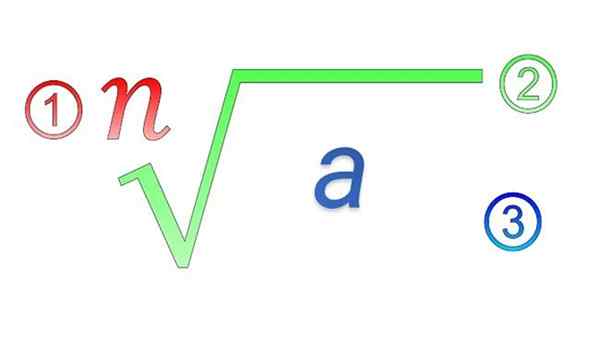
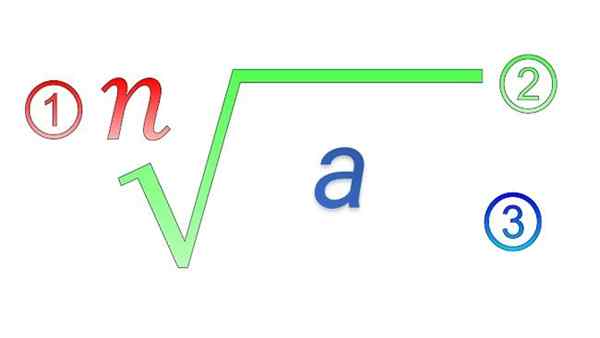Elementos radicais: 1) índice; 2) símbolo radical; 3) quantidade subradical

Quais são as propriedades dos radicais?

As propriedades radicais São operações que permitem resolver problemas complexos de radicais e poderes. O radical é a maneira de simbolizar matematicamente o n-EME de uma quantia "a". Esta raiz é outra quantia, chamada "B", de modo que seu nome seja precisamente "A", por isso é válido escrever o seguinte:

$\dpi110 \sqrt[n]a=b\Rightarrow b^n=a$

O valor de "n" é um número natural, conhecido como índice raiz, "a" é o Radicando ou quantidade subradical, e "B" é o n-EME de "A" Raiz. "A" e "B" pertencem ao conjunto de números reais.

Se o índice não for escrito em um radical, é imediatamente entendido que seu valor é igual a 2 e lê “raiz quadrada de A”.

Como "n" pertence ao conjunto de números naturais, pode ser um número ou ímpar. Então, os seguintes casos são distinguidos:

Para "n" par

Se A> 0 ou igual a 0, a raiz n-alcal de "A" é positiva ou 0 e é chamada raiz principal.
Quando < 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Para "n" estranho

Sim a> 0, o n-imem de “a” raiz é positivo.
Quando< 0, la raíz n-ésima de “a” es negativa.

Alguns exemplos são os seguintes:

$\dpi110 \sqrt49=7\Rightarrow 7^2=49$

$\dpi110 \sqrt[3]\left ( -729 \right )=-9\Rightarrow \left ( -9 \right )^3=-729$

$\dpi110 \sqrt3=1.7320508…$

Propriedades de filmagem

É possível escrever o nome de uma quantidade de uma quantidade como um poder com expoente fracionário, ou seja, um número racional.

Nesse caso, o índice raiz se torna o denominador, enquanto o expoente da quantidade subradical se torna o numerador:

Pode servir a você: Função homográfica: Como representar graficamente, exercícios resolvidos

$\dpi110 \sqrt[n]a^m=a^\fracmn$

Expressão válida enquanto n ≠ 0, pois nenhuma fração com um denominador for admitida.

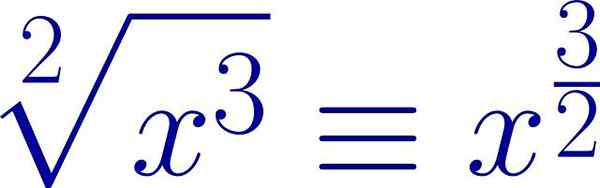Exemplo de uma expressão radical escrita na forma de um expoente fracionário. O índice raiz é o denominador do expoente, enquanto o poder da transmissão é o numerador. Fonte: Wikimedia Commons.

Dessa forma, as mesmas propriedades que se aplicam aos poderes podem ser usadas no caso de radicais.

Para valores pertencentes ao conjunto de números reais, essas propriedades são as seguintes:

1. Produto radical de igual índice

No produto de dois (ou mais) radicais do mesmo índice, as quantidades subradicais são multiplicadas, mantendo o índice:

$\dpi110 \sqrt[n]a\cdot \sqrt[n]b=\sqrt[n]a\cdot b$

2. Quociente radical do mesmo índice

O quociente entre a raiz n-essa de "a" e o n-EME de "b", sendo b ≠ 0, é igual à raiz n-ememasy do quociente entre "a" e "b":

$\dpi110 \frac\sqrt[n]a\sqrt[n]b=\sqrt[n]\fracab$

3. Raiz raiz

Para encontrar a raiz N-emeasy do M-EME da quantidade "A", a quantidade subradical é escrita sob uma raiz cujo índice é o produto entre "N" e "M":

$\dpi110 \sqrt[n]\sqrt[m]a=\sqrt[n\cdot m]a$

O procedimento é facilmente estendido a raízes sucessivas aninhadas. O índice raiz resultante é o produto de todos os índices, como este:

$\dpi110 \sqrt[n]\sqrt[m]\sqrt[p]\sqrt[q]a=\sqrt[n\cdot m\cdot p\cdot q]a$

4. Poder da raiz

N-isto, elevado ao poder M, expressa a quantidade subradical ao referido poder:

$\dpi110 \left ( \sqrt[n]a \right )^m=\sqrt[n]a^m=a^\fracmn$

Casos particulares:

1) Sim n = m, O sinal da raiz desaparece, deixando a base elevada à potência 1:

$\dpi110 \left ( \sqrt[n]a \right )^n=\sqrt[n]a^n=a$

Que é válido para ≥ 0. Em geral, se o índice raiz for um número par, você tem:

$\dpi110 \left ( \sqrt[n]a \right )^n=\left| a\right|$

(Veja exemplos mais tarde)

2) Sim m> n, A fração m/n é imprópria e a raiz pode ser simplificada, por exemplo, procurando a fração equivalente a m/n, de modo que o numerador e o denominador sejam primos entre si, ou reescreindo a quantidade subradical e aplicando algumas das propriedades descritas aqui.

Pode atendê -lo: prismas e pirâmides

(Veja exemplos mais tarde)

5. Amplificação radical

Um radical pode ser amplificado por um fator q, Se o índice radicular, bem como o poder da quantidade subradical, multiplicar pelo referido fator, e esta operação não implica a modificação do resultado. Portanto:

$\dpi110 \sqrt[n]a^m=\sqrt[n\cdot q]a^m\cdot q$

Desde que um ≥ 0 quando for mesmo.

6. Introdução de um fator dentro de um radical

Se um fator “B” positivo estiver multiplicando um radical, ele pode passar nele, se subir para o mesmo índice raiz. Em tal caso:

$\dpi110 b\sqrt[n]a^m=\sqrt[n]b^n\cdot a^m$

7. Soma e subtração de radicais

Os radicais podem adicionar e subtrair, desde que sejam o mesmo índice e tenham a mesma quantidade sub -rradica.

Quando dois ou mais radicais são de igual índice e quantidade subradical, diz -se que eles são Radicais semelhantes.

Por exemplo, os seguintes radicais são semelhantes:

$\dpi110 \sqrt[3]5,\: -7\sqrt[3]5,\: 10\sqrt[3]5$

Em vez disso, esses radicais não são semelhantes, porque não têm a mesma quantidade subradical:

$\dpi110 \sqrt2,\: \sqrt3$

Nem esses dois são semelhantes:

$\dpi110 \sqrt7,\: \sqrt[4]7$

Já que o índice radical não é o mesmo.

Radicais semelhantes podem ser reduzidos a um, adicionando ou subtraindo os coeficientes que os acompanham.

Exemplos de propriedades radicais

Exemplo 1

Qual é o valor das seguintes raízes?

$\dpi110 \sqrt32,\: \sqrt[3]-8,\: \sqrt[4]81,\: \sqrt-8$

A raiz quadrada de 32 pode ser encontrada diretamente com a ajuda da calculadora. Seu valor é:

$\dpi110 \sqrt32=5.656854249…$

Os pontos suspeitos indicam que existem decimais infinitos.

Se você preferir não trabalhar com números decimais, a raiz quadrada de 32 também pode ser calculada pela decomposição de 32 em seus principais fatores:

32 = 2⁵

Dessa forma, ao substituir, é obtido:

Pode atendê -lo: divisores de 8: o que são e uma explicação fácil

$\dpi110 \sqrt32=\sqrt2^5$

Escrito como um expoente fracionário:

$\dpi110 \sqrt32=\sqrt2^5=2^\frac52$

A fração 5/2 é imprópria, portanto o radical pode ser simplificado, usando as propriedades dos poderes:

$\dpi110 \sqrt32=\sqrt2^5=\sqrt2\cdot 2^4$

Agora aplicando a propriedade 1 acima:

$\dpi110 \sqrt2\cdot 2^4=\sqrt2\cdot \sqrt2^4=\sqrt2\cdot \sqrt16=4\sqrt2$

Portanto:

$\dpi110 \sqrt32=4\sqrt2$

Por sua parte:

$\dpi110 \sqrt[3]-8=-2$

Desde (-2)³ = −8.

De acordo com a propriedade 4:

$\dpi110 \sqrt[4]81=\sqrt[4]3^4=3$

E, finalmente, a raiz quadrada de -8 não existe no conjunto de números reais, embora nos números complexos.

Exemplo 2

Dada a seguinte operação:

$\dpi110 4\sqrt8+\sqrt81-3\sqrt32$

É possível reduzir o resultado?

Desde que os radicais sejam semelhantes, é possível reduzi -los, mas para isso eles devem ter o mesmo índice e a mesma quantidade subradical. No exemplo anterior, foi visto que:

$\dpi110 \sqrt32=4\sqrt2$

Um procedimento análogo pode ser usado para escrever a primeira adição, para que a quantidade subradical seja igual a 2:

$\dpi110 4\sqrt8=4\sqrt2^3=4\sqrt2^2\cdot 2=4\sqrt2^2\cdot \sqrt2=4\cdot 2\cdot\sqrt2=8\sqrt2$

Este radical é semelhante ao anterior. Quanto à raiz quadrada de 81, este é 9, portanto:

$\dpi110 4\sqrt8+\sqrt81-3\sqrt32=8\sqrt2+9-3\cdot 4\sqrt2=8\sqrt2+9-12\sqrt2=(8-12)\sqrt2+9=-4\sqrt2+9$

Exemplo 3

Quais propriedades são necessárias para se inscrever para realizar esta operação?

$\dpi110 \sqrt[3]x\sqrtx$

Devemos aplicar as propriedades 3 e 5, que são, respectivamente, raiz de uma raiz e introdução de um valor radical. Primeiro, a propriedade 5 se aplica, para apresentar o "X" que está fora da raiz mais interna:

$\dpi110 \sqrt[3]x\sqrtx=\sqrt[3]\sqrtx^2\cdot x=\sqrt[3]\sqrtx^3$

E agora a expressão está pronta para aplicar a propriedade 3 e multiplicar os respectivos índices de cada radical:

$\dpi110 \sqrt[3]x\sqrtx=\sqrt[3]\sqrtx^2\cdot x=\sqrt[3]\sqrtx^3=\sqrt[6]x^3$

Referências

Gonzales, d. 2011. Álgebra básica: teoria e prática. 2º. Edição.
Haeussler, e. 2012. Pré -cálculo. 1º. Edição. Pearson.
Khan Actaem. Expoentes e radicais. Recuperado de: Khanacademy.org.
Larson, r. 2012. Pré -cálculo. 8º. Edição. Cengage Learning.
Stewart, J. 2007. Matemática para cálculo. 5 ª. Edição. Cengage Learning.