Características de programação dinâmica, exemplo, vantagens, desvantagens

O Programaçao dinamica É um modelo de algoritmo que resolve um problema complexo dividindo -o em subproblemas, armazenando seus resultados para evitar ter que calcular esses resultados.

Este programa é usado quando os problemas podem ser divididos em subproblemas semelhantes, para que seus resultados possam ser reutilizados. Para a maior parte, este programa é usado para otimização.

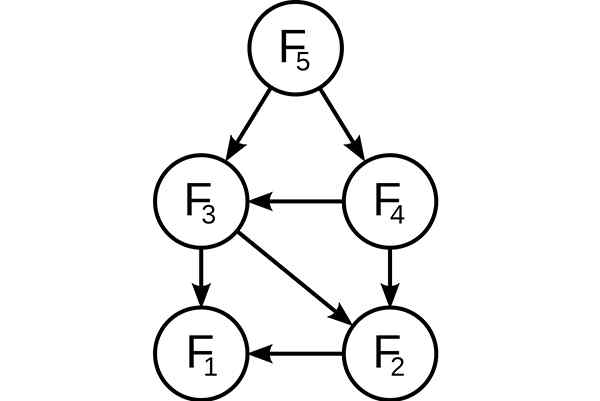
Programaçao dinamica. Subproblemas sobrepostos na sucessão de Fibonacci. Fonte: Wikimedia Commons, em: Usuário: DCOATZEE, rastreado pelo usuário: domínio stannered / público

Antes de resolver o subproblema disponível, o algoritmo dinâmico tentará examinar os resultados dos subproblemas previamente resolvidos. As soluções de subproblemas são combinadas para alcançar a melhor solução.

Em vez de calcular o mesmo subproblema repetidamente, sua solução pode ser armazenada em alguma memória, quando você conhece este subproblema. Quando aparecer novamente durante a solução de outro subproblema, a solução já armazenada na memória será tomada.

Esta é uma ideia maravilhosa para corrigir o tempo com a memória, onde, ao usar espaço adicional, você pode melhorar o tempo necessário para encontrar uma solução.

[TOC]

Características da programação dinâmica

As seguintes características essenciais são aquelas que um problema pode ser aplicado para programação dinâmica:

Subestrutura ideal

Essa característica expressa que um problema de otimização pode ser resolvido combinando as soluções ideais dos problemas secundários que compensam. Essas subestruturas ideais são descritas por recursão.

Por exemplo, em um gráfico, uma subestrutura ideal será apresentada na rota mais curta que vai de um vértice para um vértice t:

Isto é, nesta rota mais curta r, você pode tomar qualquer vértice intermediário i. Se R é realmente a rota mais curta, poderá ser dividida no Subrutas R1 (de S a I) e R2 (de I a T), para que estas sejam, por sua vez, as rotas mais curtas entre os vértices correspondentes correspondentes.

Portanto, para encontrar as rotas mais curtas, você pode formular facilmente a solução recursivamente, que é o que o algoritmo Floyd-Warshall faz.

Subproblemas sobrepostos

O espaço dos subproblemas deve ser pequeno. Ou seja, qualquer algoritmo recursivo que resolve um problema deve resolver os mesmos subproblemas repetidamente, em vez de gerar novos subproblemas.

Por exemplo, para gerar a série Fibonacci, essa formulação recursiva pode ser considerada: fn = f (n-1) + f (n-2), tomando como um caso básico que f1 = f2 = 1. Então você terá que: f33 = f32 + f31 e f32 = f31 + f30.

Como pode ser visto, o F31 está sendo resolvido nas sub -finas recursivas de F33 e F32. Embora o número total de subproblemas seja realmente pequeno, se uma solução recursiva for adotada, pois isso acabará resolvendo os mesmos problemas repetidamente.

Pode atendê -lo: os 7 componentes de um sistema de informação

Isso é levado em consideração por programação dinâmica, então resolve cada subproblema apenas uma vez. Isso pode ser alcançado de duas maneiras:

Top abordagem

Se a solução para qualquer problema puder ser formulada recursivamente usando a solução de seus subproblemas e, se esses subproblemas se sobreporem, as soluções para os subproblemas poderão ser facilmente memorizadas ou armazenadas em uma tabela em uma tabela.

Toda vez que a solução de um novo subproblema é procurada, ela será revisada na tabela se resolvida anteriormente. Caso uma solução seja armazenada, ela será usada em vez de calculá -la novamente. Caso contrário, o subproblema será resolvido, armazenando a solução na tabela.

Abordagem ascendente

Depois que a solução de um problema é recursivamente formulada em termos de seus subproblemas, o problema pode ser tentado em uma operação: primeiro eles tentarão resolver os subproblemas e usar suas soluções para alcançar soluções para os maiores subproblemas.

Isso também é geralmente feito na forma de uma tabela, gerando soluções iterativas para subproblemas cada vez mais grandes usando soluções para pequenos subproblemas. Por exemplo, se os valores de F31 e F30 já são conhecidos, o valor de F32 poderá ser calculado diretamente.

Comparação com outras técnicas

Um pertencimento significativo de um problema que pode ser resolvido por programação dinâmica é que ela deveria ter subproblemas sobrepostos. É isso que distingue a programação dinâmica da técnica de dividir e conquistar, onde não é necessário armazenar os valores mais simples.

É semelhante à recursão, pois, ao calcular casos básicos, o valor final pode ser determinado indutivamente. Essa abordagem ascendente funciona bem quando um novo valor depende apenas de valores calculados anteriormente.

Exemplo

Etapas mínimas para atingir 1

Para qualquer número inteiro positivo "E", você pode executar qualquer uma das três etapas a seguir.

- Subtrair 1 do número. (E = e-1).

- Se for divisível por 2, é dividido por 2 (se e%2 == 0, então e = e/2).

- Se for divisível por 3, é dividido por 3 (se e%3 == 0, então e = e/3).

Com base nas etapas anteriores, você deve encontrar a quantidade mínima dessas etapas a serem tomadas e 1. Por exemplo:

- Se e = 1, resultado: 0.

- Se e = 4, resultado: 2 (4/2 = 2/2 = 1).

- Quando e = 7, resultado: 3 (7-1 = 6/3 = 2/2 = 1).

Abordagem

Você sempre pode pensar em escolher o passo que torna N o mais baixo possível e continue assim, até que atinja 1. No entanto, pode -se ver que essa estratégia não funciona aqui.

Pode atendê -lo: software comercial

Por exemplo, se E = 10, as etapas seriam: 10/2 = 5-1 = 4/2 = 2/2 = 1 (4 etapas). No entanto, a maneira ideal é: 10-1 = 9/3 = 3/3 = 1 (3 etapas). Portanto, todas as etapas possíveis que podem ser feitas para cada valor de n devem ser comprovadas, escolhendo o valor mínimo dessas possibilidades.

Tudo começa com recursão: f (e) = 1 + min f (e-1), f (e/2), f (e/3) se e> 1, tomando como um caso base: f (1 ) = 0. Tendo a equação de recorrência, você pode começar a codificar a recursão.

No entanto, pode -se observar que ele sobrepôs subproblemas. Além disso, a solução ideal para uma determinada entrada depende da solução ideal de seus subproblemas.

Como na memorização, onde as soluções dos subproblemas resolvidas são armazenadas para usá -las posteriormente. Ou como na programação dinâmica, começa a partir de baixo, avançando para o dado e. Em seguida, ambos os códigos:

Memorização

Programação dinâmica para cima

Vantagens

Uma das principais vantagens do uso de programação dinâmica é que ele acelera o processamento, uma vez que as referências que foram calculadas anteriormente são usadas. Como é uma técnica de programação recursiva, reduz as linhas de código do programa.

Vorace Algoritmos vs Programação Dinâmica

Algoritmos vorazes são semelhantes à programação dinâmica no sentido de que ambas são ferramentas para otimização. No entanto, o algoritmo Voraz busca uma solução ideal em cada etapa local. Isto é, busca uma escolha gananciosa com a esperança de encontrar um ótimo global.

Portanto, algoritmos vorazes podem fazer uma suposição que parece ideal naquele momento, mas que se torna caro no futuro e não garante um ideal global ideal.

Por outro lado, a programação dinâmica encontra a solução ideal para subproblemas e depois faz uma escolha informada combinando os resultados desses subproblemas para realmente encontrar a solução mais ideal.

Desvantagens

- É necessária muita memória para armazenar o resultado calculado de cada subproblema, sem poder garantir que o valor armazenado seja usado ou não.

- Muitas vezes, o valor da saída é armazenado sem nunca ser usado nos seguintes subproblemas durante a execução. Isso leva ao uso desnecessário da memória.

- Na programação dinâmica, as funções são chamadas recursivamente. Isso faz com que a memória da bateria permaneça em aumento constante.

Recursividade versus programação dinâmica

Se você tem memória limitada para executar o código e a velocidade de processamento não é preocupante, a recursividade pode ser usada. Por exemplo, se um aplicativo móvel estiver sendo desenvolvido, a memória é muito limitada para executar o aplicativo.

Pode atendê -lo: dispositivos mistos: características e exemplos

Se o programa for desejado para ser executado mais rapidamente e não houver restrições de memória, é preferível usar programação dinâmica.

Formulários

A programação dinâmica é um método eficaz para resolver problemas que, de outra forma, poderiam parecer extremamente difíceis de resolver em um tempo razoável.

Algoritmos baseados no paradigma de programação dinâmica são usados ​​em muitas áreas científicas, incluindo muitos exemplos de inteligência artificial, desde a resolução de problemas de planejamento até o reconhecimento de voz.

Algoritmos de programação dinâmica

A programação dinâmica é bastante eficaz e serve muito bem para uma ampla gama de problemas. Muitos algoritmos podem ser vistos como aplicações de algoritmos vorazes, como:

- Série de números de Fibonacci.

- Hanói Towers.

- Todas as rotas mais curtas pares de Floyd-Warshall.

- Mochila.

- Programação do projeto.

- O caminho mais curto de Dijkstra.

- Controle e controle de vôo de robótica.

- Problemas de otimização matemática.

- Tempo compartilhado: programe o trabalho para maximizar o uso da CPU.

Série de números de Fibonacci

Os números de Fibonacci são os números encontrados na seguinte sequência: 0, 1, 1, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.

Na terminologia matemática, a sucessão de fibonacci é definida pela fórmula de recorrência: f (n) = f (n -1) + f (n -2), onde f (0) = 0 e f (1) = 1.

Top abordagem

Neste exemplo, uma matriz de pesquisa com todos os valores iniciais é inicializada com -1. Sempre que a solução para um subproblema for necessária, ela será procurada primeiro nesta matriz de pesquisa.

Se houver o valor calculado, esse valor será retornado. Caso contrário, o resultado será calculado para armazená -lo na matriz de pesquisa e, portanto, poderá reutilizá -lo mais tarde.

Abordagem ascendente

Nesse caso, para a mesma série Fibonacci, F (0), depois F (1), F (2), F (3) e assim por diante é calculado primeiro. Assim, as soluções dos subproblemas do fundo serão construídas.

Referências

1. Vineet Choudhary (2020). Introdução à programação dinâmica. UNVENVIDADO INSIDER.Retirado de: DeveloperInsider.co.
2. Alex Allain (2020). Programação dinâmica em C++. C Programação. Retirado de: cprogrammming.com.
3. Depois da Academia (2020). Ideia de programação dinâmica. Retirado de: Afteracademy.com.
4. Aniruddha Chaudhari (2019). Programação e recursão dinâmica | Diferente. Pilha CSE. Retirado de: Csestack.org.
5. Code Chef (2020). Para tutorial de programação dinâmica. Retirado de: Codhef.com.
6. Programiz (2020). Programaçao dinamica. Retirado de: Programiz.com.