Prisma quadrado

Explicamos o que é um prisma quadrangular, suas características, rostos, vértices, bordas, como calcular o volume, exemplos e exercícios resolvidos

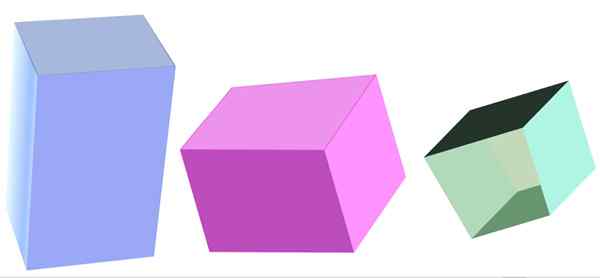
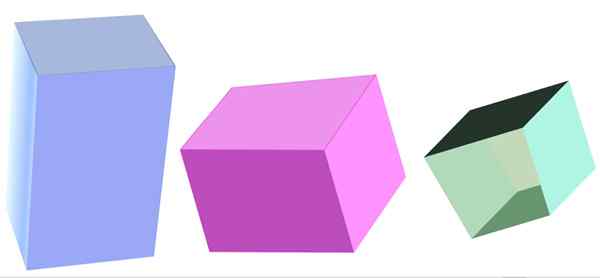Vários tipos de prisma quadrangular. Fonte: f. Zapata

O que é um prisma quadrangular?

Ele Prisma quadrado É uma figura geométrica tridimensional da família Polyhedros. É composto de duas faces iguais e paralelas, com a forma de um quadrilátero, como base e quatro paralelogramas nas laterais, para um total de seis faces.

Existem vários critérios para classificá -los, pois existem muitas possibilidades para a forma de rostos e inclinação. Por exemplo, existem Prismas diretos home run e os prismas quadrangulares inclinados.

No primeiro caso, os lados são perpendiculares à base e depois são retângulos ou quadrados. No segundo caso, as faces laterais são inclinadas em relação à base, portanto, não podem ser retângulos ou quadrados.

Além disso, o prisma quadrangular pode ser regular ou irregular, dependendo da base é um quadrilateral regular ou irregular. O quadrilátero regular é o quadrado, cujos quatro lados e seus quatro ângulos medem iguais .

Um exemplo de prisma especial em home run é o paralelepípedo, cujas bases são paralelogramas. As formas das caixas e tijolos são inspiradas por prismas quadrangulares, então bons exemplos de como usar essa figura geométrica em aplicações práticas são.

Características do prisma quadrangular

Entre as características mais importantes do prisma quadrangular estão as seguintes:

• Seus rostos têm uma forma de polígono.
• Possui um total de 6 faces (2 bases e 4 lados), 12 arestas ou bordas e 8 vértices (cantos).
• As faces laterais podem ser moldadas como: quadrado, retângulo, paralelograma, rombus ou romboide.
• Seus lados podem ser retos (formulário de 90º ângulo com as bases) ou inclinados (há um ângulo menor que 90º no lado interno).
• Os rostos laterais de prismas retos só podem ser quadrados ou retângulos.
• As bases de prisma também recebem o nome de diretrizes.
• Se a base é um quadrilateral regular, o prisma quadrangular também é regular. Como uma figura plana é regular se todos os seus lados tiverem a mesma medida, a única possibilidade é que as bases sejam quadradas.
• Quando a base do prisma é qualquer outro quadrilateral diferente do quadrado, então o prisma é considerado irregular.
• O prisma quadrangular regular pode ser registrado em um cilindro.

Pode servir a você: Estatísticas inferenciais: história, características, para que serve, exemplos

Elementos do prisma quadrangular

Os cinco elementos do prisma quadrangular são comuns a todos os prismas:

• Bases, constituído por dois quadriláteros idênticos e paralelos.
• Rostos laterais, são os quatro paralelogramas que fazem fronteira com a figura.
• Vértices ou cantos, pontos comuns que têm três lados adjacentes do prisma.
• Arestas ou bordas, segmento comum que possui dois rostos adjacentes.
• Altura: É o comprimento de um segmento perpendicular com pontas nas bases. Quando o prisma é reto, a altura coincide com a medida das bordas laterais.
• Seção reta, área de interseção entre o prisma e um plano que forma 90º com as bordas laterais.

A imagem a seguir mostra cada um desses elementos para um prisma quadrangular reto:

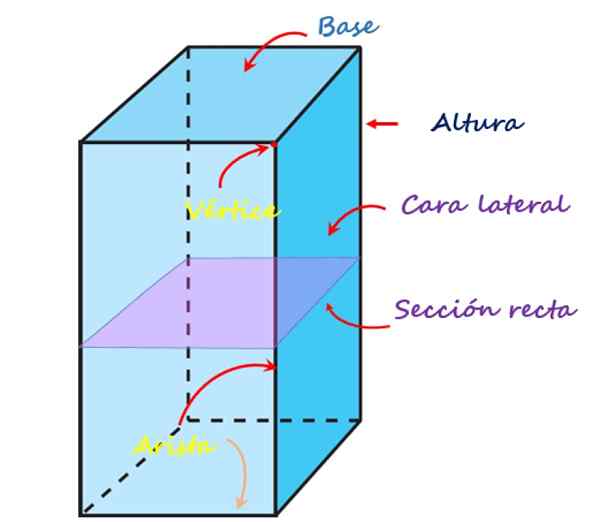Os elementos do prisma quadrangular. Fonte: f. Zapata

Rostos, vértices e bordas

De grande importância para estudar o prisma quadrangular são os rostos, os vértices e as bordas:

Rostos

As faces do prisma ganham um total de 6: as 2 bases idênticas na forma de um quadrilateral e os 4 lados lados ou faces na forma de paralelogramo.

Vértices

Eles são os cantos da figura, o ponto em que três rostos adjacentes vêm.

Arestas

Eles são os segmentos de interseção entre os rostos do prisma. As bordas são classificadas como:

• Bordas básicas, Segmentos comuns entre bases e rostos laterais.
• Bordas laterais, Como o nome indica, eles são os segmentos comuns entre as faces laterais.

A figura superior mostra os dois tipos de bordas, designados com diferentes setas coloridas. O número de arestas n_PARA pode ser determinado com o Teorema de Euler dos poliedros, que relacionam o número de arestas com o dos rostos n_C e vértices n_V:

Pode atendê -lo: funções matemáticas

N_PARA = N_C + N_V −2

Para o prisma quadrangular n_C = 6 e n_V = 8, portanto:

N_PARA = 6 + 8 −2 = 12

Portanto, o número de bordas ou bordas do prisma quadrangular é 12.

Como calcular o volume de um prisma quadrangular?

O volume do prisma é entendido como a parte do espaço bloqueado por ele e é medido em unidades cúbicas, que podem ser metros cúbicos, centímetros cúbicos, pés cúbicos ou outros apropriados, desde que eles tenham duração do cubo do cubo.

O volume V é sempre uma quantidade positiva e, no caso de qualquer prisma quadrangular, é dado pelo produto entre a base da base para_b e altura h:

V = a_b × h

Yo) Volume regular de prisma quadrangular

Como as bases são quadradas e o quadrado do quadrado é o seu lado ℓ quadrado:

PARA_b = ℓ²

Então, o volume do prisma cuja altura é "h" é:

V = ℓ² × h

Ii) Volume irregular de prisma quadrangular

Depende da forma da base e da altura "H" do prisma:

1.- Prisma da base retangular

A área do retângulo dos lados "A" e "B" é:

PARA_b = A × b

Portanto, o volume é:

V = a × b × h

2.- PRISM BASE ROMBOIDAL

A área de Rhombus é o semi -produto de suas diagonais “D” e “D”:

E o volume é:

3.- Prisma de base em forma de romboide

A área de base em forma de romboide é o produto de sua base "B" e sua altura relativa "H_r”Para esta base, que é o segmento perpendicular que vai dessa base para o lado paralelo.

PARA_b = B × h_r

Portanto, o volume do prisma com esta base é:

Pode atendê -lo: qual é o intervalo de estatísticas? (Com exemplos)

V = b × h_r × h

4.- Prisma da base trapezoidal

Como a área do trapézio é o semi -local dos lados paralelos "A" e "B", multiplicado por sua altura "C":

O volume do prisma trapezoidal é:

5.- Prisma de base em forma de trapézio

A área de um trapézico simétrico é o semi -produto de seus diagonais D e D, portanto:

Nesse caso, o volume do prisma é:

Exercício resolvido

Um prisma quadrangular da base trapezoidal tem um volume de 648 cm³. Os lados paralelos do trapézio medem a = 10 cm e B = 5 cm, enquanto a altura do trapézio é C = 6 cm. Com esses dados, encontre a altura do prisma.

Solução

Como as dimensões da base têm, sua área pode ser facilmente calculada:

E da fórmula:

V = a_b × h

"H" é limpo, a altura do prisma, uma vez que seu volume é conhecido:

H = v/ a_b = 648 cm³ / 45 cm² = 14.4 cm

Exemplos

Prisma ou cubo retangular

As seis faces deste prisma direto são quadradas ou retangulares. As caixas são exemplos de prismas retangulares, uma forma que também é usada em vários objetos e construções, como edifícios.

Cubo

Um cubo é um prisma quadrangular regular, cujos seis lados têm a forma de um quadrado, por exemplo, um dado ou o jogo de cubo de Rubik, bem conhecido.

O cubo faz parte do grupo de sólidos platônicos, figuras geométricas que atendem a duas condições. A primeira é que cada face é um polígono regular e o segundo é que cada vértice tem em comum o mesmo número de faces.

O cubo atende a ambas as condições, pois seus rostos têm uma forma quadrada, que é um polígono comum. E em cada um dos oito vértices do cubo, três faces da mesma conversa.

Os sólidos platônicos restantes são o tetraedro, o octaedro, o dodecaedro e o icosaedro.