Y = período da função 3sen (4x)

Ele Y = período da função 3sen (4x) É 2π/4 = π/2. Para entender claramente o motivo dessa declaração, a definição de um período de uma função e o período da função sen (x) devem ser conhecidos; Um pouco sobre o gráfico de funções também será útil.

As funções trigonométricas, como seio e cosseno (sen (x) e cos (x)), são muito úteis em matemática e engenharia.

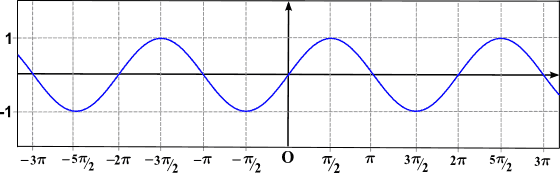
O período da palavra menciona a repetição de um evento; portanto, dizer que uma função é periódica é equivalente a dizer “seu gráfico é a repetição de uma peça de curva”. Como pode ser visto na imagem anterior, a função sen (x) é periódica.

Funções periódicas

Diz -se que uma função f (x) é periódica se houver um valor real p ≠ 0 tal que f (x+p) = f (x) para todos os x no domínio da função. Nesse caso, o período da função é p.

Geralmente é chamado de período da função no número real mais baixo positivo P que satisfaz a definição.

Como pode ser visto no gráfico anterior, a função sen (x) é periódica e seu período é 2π (a função cosseno também é periódica, com um período igual a 2π).

Alterações no gráfico de uma função

Seja f (x) uma função cujo gráfico é conhecido e seja c uma constante positiva. O que acontece com o gráfico de f (x) se multiplicar F (x) por C? Em outras palavras, como é o gráfico de c*f (x) e f (cx)?

C*f Gráfico (x)

Ao multiplicar uma função, externamente, por uma constante positiva, o gráfico de f (x) passa por uma alteração nos valores de saída; Ou seja, a mudança é verticalmente e dois casos podem ser tomados:

- Se C> 1, o gráfico sofre um alongamento vertical com um fator C.

- Sim 0

F Graph (CX)

Quando o argumento de uma função é multiplicado por uma constante, o gráfico de f (x) sofre uma alteração nos valores de entrada; Ou seja, a mudança é horizontalmente e, como antes, dois casos podem ser tomados:

- Se c> 1, então o gráfico sofre uma compressão horizontal com um fator de 1/c.

- Sim 0

Y = período da função 3sen (4x)

Deve -se notar que na função f (x) = 3se (4x) existem duas constantes que alteram o gráfico da função sinusal: um multiplicando externo e outro de maneira interna.

O 3 que está fora da função seno é estender a função verticalmente por um fator de 3. Isso implica que o gráfico da função 3Sen (x) estará entre os valores -3 e 3.

O 4 que está dentro da função seno torna a função gráfica uma compressão horizontal para um fator 1/4.

Por outro lado, o período de uma função é medido horizontalmente. Como o período da função sen (x) é 2π, ao considerar o pecado (4x), o tamanho do período mudará.

Para saber qual é o período de y = 3sen (4x) apenas multiplicar o período da função Sen (x) por 1/4 (o fator de compressão).

Em outras palavras, o período da função y = 3sen (4x) é 2π/4 = π/2, como pode ser visto nos últimos gráficos.