Enquanto uma fórmula e equações de linha, representação, exemplos

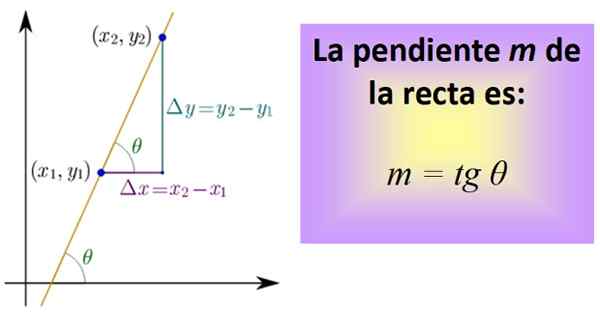
O linha pendente É a tangente do ângulo θ que essa linha forma com o eixo horizontal, que por convenção é medido na direção oposta às mãos do relógio. A inclinação de qualquer linha é sempre constante e é por isso que é uma de suas características mais essenciais.

Para calculá -lo, você precisa saber dois pontos da linha, cujas coordenadas são (x x₁,e₁) e (x₂,e₂). Entre os dois pontos, é desenhado um segmento que pertence à linha e depois aos segmentos que representam a distância entre x são desenhados₁ e x₂, e entre e₁ e e₂, Como na figura inferior.

figura 1. A inclinação de uma linha é a tangente do ângulo θ. Fonte: Wikimedia Commons.

Os três segmentos compõem um triângulo certo cujas pernas são: Δx = x₂ - x₁  e Δy = e₂ - e₁. Eles correspondem respectivamente a um deslocamento horizontal e outro vertical.

Agora um quociente é definido, chamado tangente do ângulo θ e abreviado tg θ, que é precisamente a inclinação m da linha:

m = tg θ = Δy / Δx

Observe que, para uma linha, esse ângulo permanece constante, independentemente dos pontos tomados para calcular sua tangente. De qualquer forma, esse valor nos oferece uma medida de quão inclinado é a linha.

Através das coordenadas dos pontos selecionados, a fórmula da inclinação permanece:

M = (y - y₁ ) / (X₂ - x₁)

[TOC]

Representação gráfica

Abaixo, temos várias situações em que o conceito de inclinação é relevante. Seu valor pode ser facilmente calculado medindo o respectivo deslocamento vertical e horizontal e, em seguida, fazendo o quociente indicado no início.

Isso nos dá uma idéia da inclinação ou do declínio de alguma estrutura, como uma rampa, um teto ou uma estrada:

Pode servir a você: Amostragem aleatória: metodologia, vantagens, desvantagens, exemplos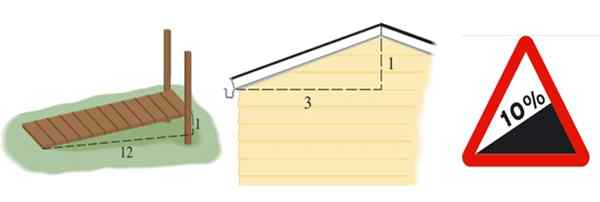 Figura 2. Da esquerda para a direita a inclinação de uma rampa, um teto e a inclinação de uma estrada, a última expressa em porcentagem. Fonte: Stewart, J. Precáculculo e Wikimedia Commons (imagem direita).

A inclinação da rampa mostrada na Figura 2 à esquerda é m = 1/12, o teto é m = 1/3 e a estrada é expressa em porcentagem. Uma porcentagem de 10 % significa que, a cada 100 metros que avança horizontalmente, eles ganham 10 metros de altura:

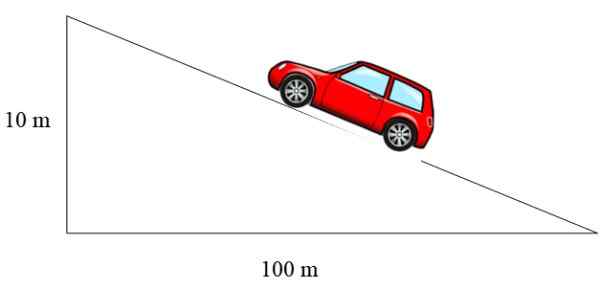Figura 3. Um veículo sobe através de uma inclinação cuja ladeira é 10%. Fonte: f. Zapata.

Nesse caso, a inclinação é 10/100 = 0.1, que expresso como uma porcentagem é igual a 10%.

Tipos de inclinação

A inclinação de uma linha pode ser positiva, negativa ou nula. Por exemplo, a linha mostrada na Figura 1 tem uma inclinação positiva. Agradecemos imediatamente porque vemos que a linha é "levantada" se a veremos da esquerda para a direita.

Se a linha descer descer vê -la da esquerda para a direita, então sua inclinação é negativa. E quando uma linha é horizontal, sua inclinação é nula.

Finalmente, para linhas verticais, a inclinação não é definida.

A representação gráfica de cada tipo é encontrada abaixo:

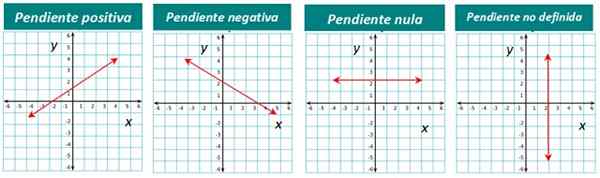Figura 4. As linhas de acordo com sua inclinação. Fonte: f. Zapata.

Como a inclinação é calculada uma linha?

Cálculo da inclinação é muito simples, você só precisa encontrar deslocamento vertical e deslocamento horizontal e depois fazer o quociente entre os dois.

Quando você tem o desenho da linha no avião cartesiano, esses deslocamentos estão escolhendo dois pontos da linha P₁ E P₂, Determinando suas coordenadas e aplicando a definição dada no início:

Pode atendê -lo: o que representa o comprimento do deslocamento hexagonal

M = (y - y₁ ) / (X₂ - x₁ )

Como o valor da inclinação é independente da escolha de P₁ E P₂ , Vamos escolher um ponto P de coordenadas (x, y) que pertence à linha, cujas coordenadas não são conhecidas, e outro ponto P₁ cujas coordenadas são: (x₁,e₁).

A inclinação é:

M = (y - y₁) / (x - x₁)

Podemos limpar o e:

e e₁ = m (x - x₁)

Agora suponha que o ponto P₁ É a interseção da linha com o eixo vertical, de coordenadas (0, b). Substituindo isso na equação anterior:

e - b = m (x - 0) → y = mx + b

Esta expressão é conhecida como a equação da linha na forma Pendente - interseção, Como a linha é inequivocamente determinada quando sua inclinação e interseção com o eixo vertical são conhecidos.

Saber que apenas a inclinação não é suficiente para caracterizar uma linha no avião, já que a reta infinita pode ter a mesma inclinação, o que significa que elas são paralelas, mas passam por outros pontos.

Exercícios resolvidos

- Exercício 1

Encontre a inclinação da linha mostrada na figura a seguir:

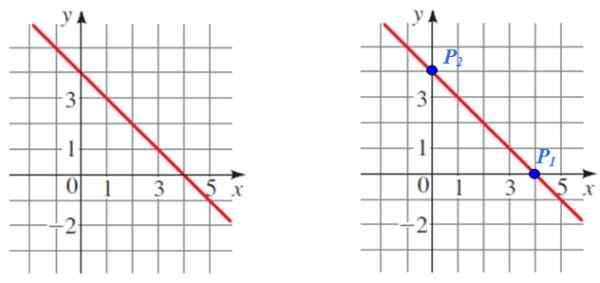Figura 5. Através do gráfico de uma linha, dois pontos são escolhidos para calcular sua inclinação. Fonte: f. Zapata.

Solução

P₁ E P₂ Eles são dois pontos de leitura fácil -que servirão para o cálculo, também observa que eles são as respectivas interseções com os eixos de coordenadas.

As coordenadas de cada ponto são:

P₁ (4.0) e P₂ (0,4)

Substituindo a equação da inclinação:

M = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

A inclinação é negativa, o que era esperado após observar os gráficos.

Pode atendê -lo: números complexos: propriedades, exemplos, operações

- Exercício 2

Encontre a equação da linha que passa pelo ponto (1, -6) e é paralela à linha y = 2x - 3.

Solução

A inclinação da linha procurada deve ser a mesma que a de y = 2x - 3, pois são paralelas. Para esta linha, a inclinação é m = 2, portanto, a que estamos procurando tem o formulário:

e e₁ = 2 (x - x₁)

Agora substituímos o ponto pelo qual nossa linha passa: x₁ = 1 e₁ = -6.

e - (-6) = 2 (x - 1)

Portanto y = 2x - 2 - 6 → y = 2x - 8

Exemplos

Duas quantidades podem estar relacionadas de tal maneira que seu gráfico é uma linha reta. Nesse caso, diz -se que as quantidades têm dependência linear e a inclinação da linha pode ser interpretada como a razão da mudança de uma variável para a outra.

Exemplo 1

Suponha que uma piscina esteja cheia de água para um taxa constante no tempo. Naturalmente, quanto mais tempo passa, mais água é armazenada. Bem, a taxa à qual o pool é preenchido é precisamente a inclinação da linha que relaciona o volume ao tempo:

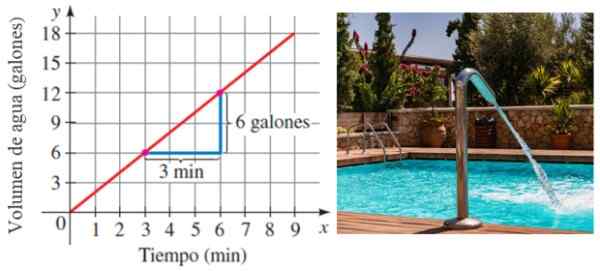Figura 6. A inclinação como motivo de mudança. Fonte: Stewart, J./Pxfuel.

Neste exemplo, a piscina é preenchida a uma taxa de 6/3 galões por minuto ou 2 galões/minuto.

Exemplo 2

Quando um celular se move em uma linha reta com velocidade constante, a inclinação do gráfico de posição depende do tempo não é outro senão a velocidade. O gráfico mostra um celular com velocidade positiva, o que significa que está se afastando da origem.

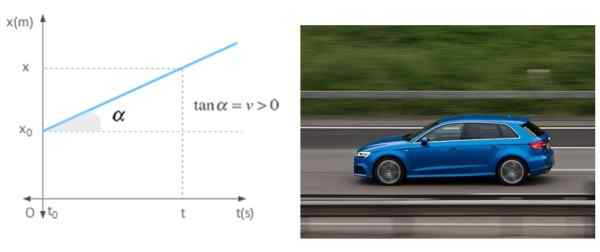Figura 7. A inclinação do gráfico versus Time é a velocidade do celular em um movimento uniforme retilíneo. Fonte: Wikimedia Commons/Pixabay.

Referências

1. Alvarez, J. A inclinação de uma estrada. Recuperado de: Geogebra.é.
2. Carena, m. 2019. Manual de matemática da pré -universidade. Universidade Nacional da Costa.
3. Hoffman, J. Seleção de questões de matemática. Volume 4.
4. Jiménez, r. 2008. Álgebra. Prentice Hall.
5. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
6. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.