Conceito linear ondas, características, exemplos

As Ondas lineares Essas são aquelas em que o princípio da superposição é aplicável, ou seja, aqueles em que a forma de onda e sua evolução espaço-tempo podem ser alcançados como a soma das soluções básicas, por exemplo, do tipo harmônico. Nem todas.

A denominação "linear" vem do fato de que ondas lineares sempre satisfazem uma equação diferencial em derivados parciais, na qual todos os termos envolvendo a variável dependente ou seus derivados são aumentados para o primeiro poder.

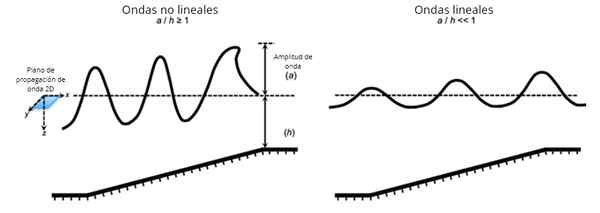
As ondas que são vistas à distância são ondas lineares, no entanto, as ondas assustadas do primeiro plano são não lineares. Fonte: Pixabay.

Por outro lado, ondas não lineares satisfazem equações de ondas com graus quadráticos ou mais altos na variável dependente ou em seus derivados.

Às vezes, é confuso para ondas lineares com ondas longitudinais, que são aquelas em que a vibração ocorre na mesma direção da propagação, como ondas sonoras.

Mas ondas longitudinais, assim como transversais, podem, por sua vez.

Geralmente ocorre que, quando o distúrbio inicial é de pequena amplitude, a equação que descreve a propagação da onda é do tipo linear ou pode ser linha por determinadas abordagens, embora nem sempre seja assim.

[TOC]

Equação diferencial em ondas lineares

Em um meio linear, uma forma de onda limitada no espaço e no tempo pode ser representada pela soma de funções de onda sinusal ou cosseno de diferentes frequências e comprimentos de onda via série de Fourier. 

As ondas lineares sempre têm uma equação diferencial do tipo linear associado, cuja solução representa a previsão do que será o distúrbio nos momentos posteriores de um distúrbio inicial localizado espacialmente no instante inicial inicial.

A equação de onda linear clássica, em uma única dimensão espacial, cujas soluções são ondas lineares é:

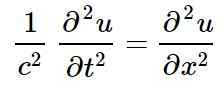
Na equação anterior ou representa a perturbação de uma certa quantidade física na posição x E no momento t, quer dizer ou É uma função de x e t:

Pode atendê -lo: o que são vetores coplanares? (Com exercícios resolvidos)

u = u (x, t)

Por exemplo, se for uma onda de som no ar, ou Pode representar a variação da pressão em relação ao seu valor sem perturbar.

No caso de uma onda eletromagnética, ou representa o campo elétrico ou o campo magnético que oscilam perpendicularmente à direção da propagação.

No caso de uma corda tensa, ou Representa o deslocamento cruzado em relação ao equilíbrio do equilíbrio da corda, como mostrado na figura a seguir:

Forma de onda em um determinado instante, no caso de ondas lineares, essa forma é a sobreposição de ondas sinusoidais de diferentes frequência e comprimentos de onda. Fonte: f. Zapata.

Soluções de equações diferenciais

Se você tiver duas ou mais soluções da equação diferencial linear, cada solução multiplicada por uma constante será uma solução e também será a soma deles. 

Ao contrário das equações não lineares, as equações de onda admitem soluções harmônicas do tipo: 

ou₁= A⋅sen (k⋅x - ω⋅t) e ou₂= A⋅sen (k⋅x + ω⋅t) 

Isso pode ser verificado por simples substituição na equação de onda linear.

A primeira solução representa uma onda progressiva que avança para a direita, enquanto a segunda à esquerda rapidamente C = ω/k.

As soluções harmônicas são características das equações de ondas lineares.

Por outro lado, a combinação linear de duas soluções harmônicas também é uma solução para a equação de onda linear, por exemplo:

u = a₁ cos (k₁⋅x - ω₁⋅t) + A₂ afundar₂⋅x - ω₂⋅t) é solução.

A característica mais relevante das ondas lineares é que qualquer forma de onda, por mais complexa, pode ser obtida por uma soma de ondas harmônicas simples em mama e cosseno:

u (x, t) = a₀ + ∑_n PARA_n cos (k_n⋅x - ω_n⋅t) + ∑_m B_m afundar_m⋅x - ω_m⋅t).

Ondas lineares dispersivas e não dispersivas

Na equação de onda linear clássica, c representa a velocidade de propagação do pulso.

Ondas não dispersivas

Nos casos onde c É um valor constante, por exemplo, as ondas eletromagnéticas no vazio, depois um pulso no momento inicial t = 0 Forma f (x) Ele se espalha de acordo com:

u (x, t) = f (x - c⋅t)

Sem sofrer nenhuma distorção. Quando isso ocorre, diz-se que o meio não é design.

Ondas dispersivas

No entanto, na mídia dispersiva, a velocidade de propagação C pode depender do comprimento de onda λ, ou seja: C = C (λ).

Pode atendê -lo: equação de continuidade

Ondas eletromagnéticas são dispersivas ao viajar por um meio material. Também as ondas de superfície da água viajam em velocidade diferente de acordo com a profundidade da água.

A velocidade com que uma onda harmônica se propaga A⋅sen (k⋅x - ω⋅t) é Ω/k = c e a velocidade de fase é chamada. Se o meio for dispersivo, então c É uma função de número de onda k: C = c (k), onde k Está relacionado ao comprimento de onda por meio de K = 2π/λ.

Relacionamentos de dispersão

A relação entre frequência e comprimento de onda é chamada Razão de dispersão, o expresso em termos de frequência angular Ω e o número da onda k é: Ω = c (k) ⋅k.

Alguns relacionamentos de dispersão As características das ondas lineares são as seguintes:

Nas ondas em que o comprimento de onda (distância entre os cumes) é muito maior que a profundidade H, Mas que sua amplitude é muito menor que a profundidade que a relação de dispersão é:

Ω = √ (gh) ⋅k

De lá, conclui -se que eles se espalharam em velocidade constante √ (gh) (metade não dispersiva).

Mas as ondas em águas muito profundas são dispersivas, uma vez que sua taxa de dispersão é:

ω = √ (g/k) ⋅k

Isso significa que a velocidade de fase Ω/k É variável e depende do número da onda e, portanto, o comprimento de onda da onda.

Velocidade do grupo

Se duas ondas lineares harmônicas se sobrepor, mas avançar em velocidades diferentes, a velocidade do grupo (ou seja, do pacote de ondas) não corresponde à velocidade da fase.

Velocidade do grupo v_g É definido como o derivado de frequência em relação ao número da onda na taxa de dispersão: v_g = Ω '(k).

A figura a seguir mostra a sobreposição ou a soma de duas ondas harmônicas ou₁= A⋅sen (k₁⋅x - ω₁⋅t) e ou₂= A⋅sen (k₂⋅x - ω₂⋅t) aquela viagem em velocidades diferentes v₁= Ω₁/k₁ e v₂= Ω₂/k₂. Observe como a velocidade do grupo é diferente da velocidade de fase, neste caso a velocidade do grupo ∆ω/∆K.

Pode atendê -lo: propriedades magnéticas dos materiais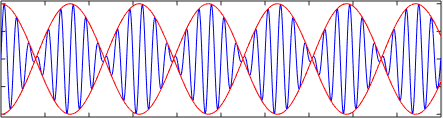Onda linear (azul) em um meio dispersivo. A curva vermelha foi adicionada para destacar que a velocidade do grupo é diferente da velocidade de propagação

Dependendo da taxa de dispersão, a velocidade de fase e a velocidade do grupo, nas direções opostas, podem até ter as direções opostas.

Exemplos de ondas lineares

Ondas eletromagnéticas

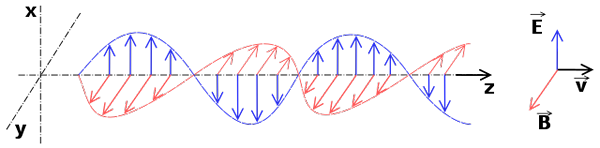ondas eletromagnéticas que compõem a radiação eletromagnética

Ondas eletromagnéticas são ondas lineares. Sua equação de onda é deduzida das equações de eletromagnetismo (equações de Maxwell) que também são lineares.

Equação de Schrödinger

É a equação que descreve a dinâmica das partículas na escala atômica, onde as características onduladas são relevantes, por exemplo, o caso de elétrons no átomo.

Em seguida, a "onda eletrônica" ou a função de onda como também é chamada, é uma onda linear.

Ondas em águas profundas

Ondas lineares também são aquelas em que a amplitude é muito menor que o comprimento de onda e o comprimento de onda muito maiores que a profundidade. As ondas em águas profundas seguem a teoria linear (conhecida como teoria ondulada de Airy).

No entanto, a onda que se aproxima da costa e forma a crista característica que é rolada (e que os surfistas amam) é uma onda não linear.

O som

Como o som é uma pequena perturbação da pressão atmosférica, é considerado uma onda linear. No entanto, a onda de choque de uma explosão ou frente de onda de um plano supersônico, são exemplos típicos de ondas não lineares.

Ondas em uma corda tensa

As ondas que se espalham por uma corda tensa são lineares, desde que a pulsação inicial seja pequena, ou seja, o limite elástico da corda não é excedido.

As ondas lineares nas cordas são refletidas em suas extremidades e se sobrepõem, dando origem a ondas estacionárias ou modos vibracionais que dão os tons harmônicos e subarmônicos característicos de instrumentos de cordas.

Referências

1. Griffiths G e Schiesser W. Ondas lineares e não lineares. Recuperado de: sholarpedia.org.
2. Whitham g.B. (1999) "Ondas lineares e não lineares". Wiley. 
3. Wikipedia. Ondas não lineares. Recuperado de: é.Wikipedia.com
4. Wikipedia. Acústico não linear. Recuperado de: em.Wikipedia.com
5. Wikipedia. Ondas. Recuperado de: em.Wikipedia.com
6. Wikiwaves. Ondas não lineares. Recuperado de: wikiwaves.org