Propriedades da série Fibonacci, relações naturais, aplicações

O O Series A sucessão de Fibonacci é uma sequência de números obtidos com o início de 0 e 1, continua com a soma deles: 0 + 1 = 1, então a soma dos dois anteriores: 1 + 1 = 2 e assim por diante.

Seguindo este procedimento, os outros termos são obtidos, vamos ver: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

Primeiro número da série Fibonacci

O procedimento é repetido quantas vezes quiser. Dessa forma, a sucessão de Fibonacci adquire o formulário: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 .. Os números que o fazem são chamados Números Fibonacci.

[TOC]

História

A sucessão de Fibonacci é chamada de matemática italiana que viveu na Idade Média: Leonardo de Pisa, também conhecido como Fibonacci (1175-1250). 

Leonardo de Pisa

Leonardo passou a infância no norte da África e viajou por todo o Mediterrâneo, onde conhecia o sistema de numeração Indo -Arábico e ficou encantado com ele. Provavelmente os professores árabes de Leonardo o ensinaram sobre a sucessão, que já era conhecida por matemáticos hindus.

Posteriormente, ao retornar a Pisa Fibonacci, escreveu um livro chamado Liber Abaci (O Livro de Abacus), onde, além de destacar as vantagens dos números Indo -Arábicos diante da numeração e introdução romana de 0, ele levantou um problema sobre a reprodução de coelhos.

E a solução para esse problema é precisamente o número de sucessão de Fibonacci.

Leonardo de Pisa não recebeu a criação da sucessão; Ele apenas mencionou isso em seu livro como uma curiosidade, que chamou a atenção de muitos estudiosos que o seguiram. Entre eles estava o matemático francês do século XIX, Edouard Lucas, que ao estudar a sucessão a batizou com o nome do sábio medieval que o tornou conhecido no Ocidente.

O problema dos coelhos de Fibonacci

O problema diz: há alguns coelhos vivendo para sempre, que em dois meses é fértil. Depois que a maturidade é alcançada, eles têm alguns bebês de sexo diferente todos os meses, que também levam dois meses para se reproduzir e ter um casal mensal de coelhos.

Pode atendê -lo: De Morgan Leis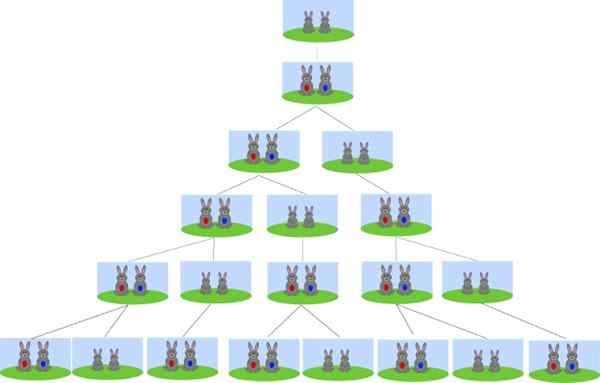A origem da sucessão de Fibonacci está no problema da reprodução de coelhos. Fonte: Wikimedia Commons.

Começando com alguns coelhos recém -nascidos, quantos pares de coelhos serão em um mês? Quantos pares de coelhos terão após 2, 3 e 4 meses? E quantos serão depois de 6 meses?

A resposta está em números de Fibonacci. Após 1 mês, há um par de coelhos, o casal original, pois eles apenas se reproduzem após 2 meses.

Após 2 meses, há 2 casais de coelhos: o casal original e sua primeira ninhada.

Aos 3 meses, teremos 3 casais, incluindo o casal original, sua primeira ninhada e um novo.

Ao chegar ao quarto mês, teremos o casal original, a primeira ninhada que, por sua vez, tem seus primeiros filhos, a ninhada do terceiro mês e uma nova ninhada. No total, 5 pares de coelhos.

Mas esses são os números da sequência de Fibonacci; portanto, após 6 meses, haverá 13 casais de coelhos, pois cada mês os casais dos dois meses anteriores são adicionados.

Propriedades da série Fibonacci

Aqui estão algumas propriedades interessantes da sucessão de Fibonacci.

Propriedade 1

A fórmula recursiva para encontrar os termos da sucessão é:

para_N+1 = a_n + para_N-1  Para n maior ou igual a 2.

Onde n = 2, 3, 4,… isto é, para encontrar o sétimo termo a₇, Nós fazemos n = 6, para que 6+1 = 7. Precisamos saber os termos para₅  já₆, da lista que aparece na introdução a₅ = 5 e um₆ = 8, portanto para₇ = 5+8 = 13.

Propriedade 2

Se os dois termos que queremos encontrar não forem conhecidos, podemos usar a seguinte fórmula:

Pode atendê -lo: Tesseldos: característica, tipos (regular, irregular), exemplos

Propriedade 3

Os números a_n já_N+1 são  Coprimos, isto é, eles são primos entre si, o que significa que eles não têm fatores comuns em comum.

Propriedade 4

Uma propriedade muito interessante é a do quociente entre os termos para_2n já_n, que vale 1, quando n = 1. Quer dizer:

para₂ / para₁ = 1

Podemos verificar facilmente com a lista de números de Fibonacci.

Por outro lado, se n ≠ 1, então o quociente é:

para_2n / para_n = a_n  + 2º_N-1

Por exemplo se n = 3, então um _2n = a₆ = 8 e₃ = 2. Pois bem:

8/2 = 2 + 2. para₂ = 2 + 2. 1

De fato: 8/2 = 4 e 2 + (2.1) = 4. Pode -se verificar se qualquer valor n é atendido.

Propriedade 5

A proporção r_n = a_N+1 / para_{n ,} Quando n se torna ótimo, converja para o Razão de ouro qualquer Proporção de aurea, Um número irracional que surge com frequência na natureza, dado por:

Relações naturais da sucessão de Fibonacci

Sucessão de Fibonacci em plantas

As manifestações da sucessão de Fibonacci abundam no reino vegetal

Os ramos de certas árvores estão saindo todos os anos, de acordo com a sucessão de Fibonacci. No primeiro ano, o porta. Por sua vez, cada ramo pode jogar outro novo depois de um ano, assim como os coelhos se reproduzem.

O Centro de Flores de Girassol contém as sementes dispostas em vigas espirais logarítmicas, em ambos os sentidos, cujas quantidades correspondem a dois números consecutivos de Fibonacci.

Os números de Fibonacci estão presentes no número de girassol e margarita de pétalas, bem como em vários padrões nos quais as plantas têm suas folhas.

Pode atendê -lo: variável ordinal

Especialistas dizem que, dessa maneira.

Com um ponto central como ponto de partida, essas estruturas crescem e recebem luz solar, portanto as novas folhas e pétalas devem cobrir o mínimo possível daqueles que saíram primeiro. E a melhor maneira de conseguir isso é adotar um padrão de crescimento em termos da sequência de Fibonacci.

Sucessão de Fibonacci em animais

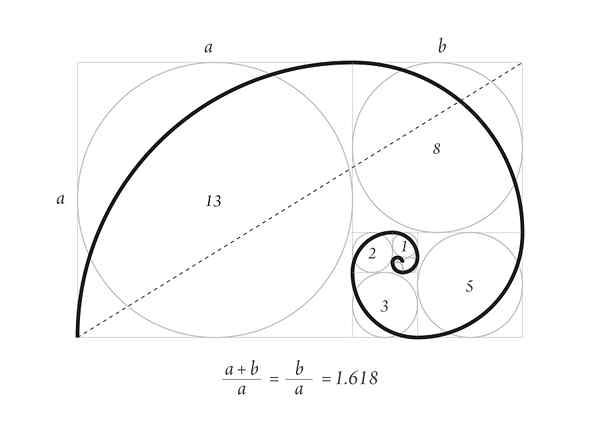A espiral de Durero com o primeiro número de sucessão de Fibonacci

A espiral durável da imagem superior faz parte do padrão de crescimento das conchas em animais marinhos e dos chifres de alguns ruminantes.

Comece com dois quadrados 1, um em cima do outro, depois um quadrado de lado 2 ao lado dele, que compõe um retângulo do lado 3, cujos lados têm a proporção dourada.

Abaixo está um quadrado de lado 3 e à esquerda um quadrado de lado 5. Acima, há um quadrado de lado 8 e à direita um quadrado de lado 13. Estes são o primeiro número da sucessão.

Finalmente a espiral é desenhada tocando os pontos dos cantos dos quadrados, como visto na figura.

Formulários

A sucessão de Fibonacci é aplicada em vários campos:

-Na arte, a proporção dourada relacionada à sucessão de Fibonacci aparece em pessoas e coisas representadas por grandes artistas como Leonardo da Vinci, Miguel Ángel e Alberto Durero.

-As proporções do parceiro em Atenas também respondem ao número de ouro.

-Nas composições de Mozart, Beethoven, Schubert e Debussy.

-Projetar objetos cujas proporções parecem harmoniosas aos olhos humanos, como cartões de crédito, contêineres, bandeiras.

-No mercado de ações, é usado para prever quais preços reverte sua tendência.

Referências

1. Sucessão de Fibonacci. Recuperado de: blogeducastur.é.
2. Stewart, J. 2007. Pré -cálculo. 5 ª. Edição. Cengage Learning.
3. Vargas, m. Aplicações de sucessão de Fibonacci. Recuperado de: Matesup.Cl.
4. Wikipedia. Número de Fibonacci. Recuperado de: em.Wikipedia.org.