Propriedades de números imaginários, aplicações, exemplos

O Números imaginários Eles são aqueles que dão solução para a equação em que o desconhecido, quadrado elevado, é igual a um número negativo real. A unidade imaginária é I = √ (-1).

Na equação: z²= - a, z É um número imaginário que é expresso da seguinte forma:

 Z = √ (-a) = i√ (a)

Ser para Um número real positivo. Sim A = 1, então z = i, onde Yo é a unidade imaginária.

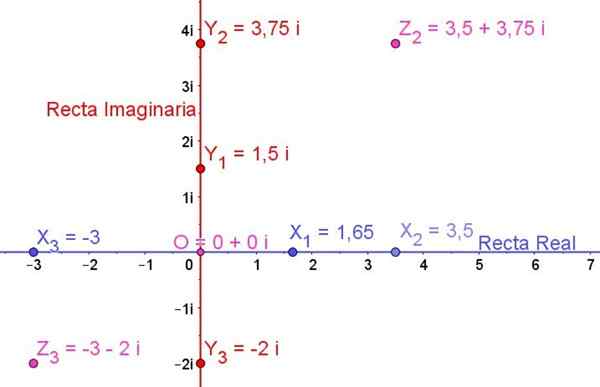figura 1. Plano complexo mostrando alguns números reais, alguns números imaginários e alguns números complexos. Fonte: f. Zapata.

Em geral, um número imaginário Z é sempre expresso em forma: 

z = y⋅i

Onde e É um número real e Yo é a unidade imaginária.

Bem como números reais são representados em uma linha, chamada de Real reto, Análogo Os números imaginários são representados no Imaginário reto.

O Imaginário reto É sempre ortogonal (forma 90º) para o Real reto e as duas linhas definem um plano cartesiano chamado Plano complexo.

A Figura 1 mostra o plano complexo e alguns números reais, alguns números imaginários e também alguns números complexos são representados nele:

X₁, X₂, X₃ Eles são números reais

E₁, E₂, E₃ Eles são números imaginários

Z₂ e z₃ Eles são números complexos

O número ou é o zero real e também é o zero imaginário, de modo que a origem ou o complexo zero expresso por:

0 + 0i 

[TOC]

Propriedades

O conjunto de números imaginários é indicado por:

I = …, -3i,…, -2i,… .,-Ei,… .,0i, .. .,Ei,… .,2i, .. .,3i,…

E algumas operações sobre esse conjunto numérico podem ser definidas. Um número imaginário nem sempre é obtido a partir dessas operações, então as veremos com um pouco mais de detalhes:

Soma e subtração do imaginário

Números imaginários podem adicionar e subtrair um do outro e, como resultado, haverá um novo número imaginário. Por exemplo:

Pode servir a você: primos relativos: o que são, explicação, exemplos

 3i + 2i = 5i

4i - 7i = -3i

Produto imaginário

Quando o produto de um número imaginário com outro é feito, o resultado é um número real. Vamos fazer a seguinte operação para verificar:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

E como vemos, o -6 é um número real, embora tenha sido obtido multiplicando dois números imaginários puros.

Produto de um número real para outro imaginário

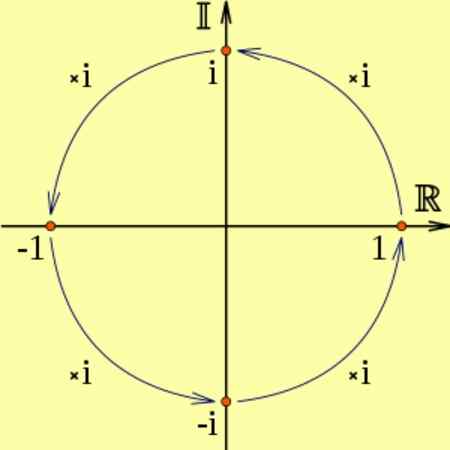
Se um número real for multiplicado por i, o resultado será um número imaginário, que corresponde a uma rotação de 90 graus.

E isso é eu² corresponde a duas rotações consecutivas de 90 graus, o que é equivalente a multiplicar por -1, ou seja, eu² = -1. Pode ser visto no seguinte diagrama:

Figura 2. A multiplicação pela unidade imaginária e corresponde a rotações 90º. Fonte: Wikimedia Commons.

Por exemplo:

-3 x 5i = -15i

-3 x i = -3i.

Potenciação de um imaginário

A potencialização de um número imaginário para um expoente inteiro pode ser definido:

Yo¹ = i

Yo² = i x i = √ (-1) x √ (-1) = -1

Yo³ = i x i² = -I

Yo⁴ = i² XI² = -1 x -1 = 1

Yo⁵ = i x i⁴ = i

Em geral você tem que Yoⁿ = i^(n mod 4), onde Mod É o resíduo da divisão entre n e 4.

A potencialização de números inteiros negativos também pode ser feita:

Yo^-1 = 1 / i¹ = i / (i x i¹) = I / (eu²) = I / (-1) = -i

Yo-² = 1 / i² = 1/ (-1) = -1

Yo-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Em geral, o número imaginário B⋅i elevado à energia n é:

(B⋅i) Iⁿ = bⁿ Yoⁿ = bⁿ i^(n mod 4)

Alguns exemplos são os seguintes:

(5 I)¹² = 5¹² Yo¹² = 5¹² Yo⁰ = 5¹² x 1 = 244140625

(5 I)^onze = 5^onze Yo^onze = 5^onze Yo³ = 5^onze x (-i) = -48828125 i

(-2 I)¹⁰ = -2¹⁰ Yo¹⁰ = 2¹⁰ Yo² = 1024 x (-1) = -1024

Soma de um número real e um imaginário

Quando um número real é adicionado com um imaginário, o resultado não é real nem imaginário, é um novo tipo de número chamado Número complexo.

Por exemplo, se x = 3,5 e y = 3,75i, o resultado é o número complexo:

Pode atendê -lo: quadrados mínimos

Z = x + y = 3,5 + 3,75 i

Observe que as partes reais e imaginárias não podem ser agrupadas na soma; portanto, um número complexo sempre terá uma parte real e outra parte imaginária.

Esta operação estende o conjunto de números reais aos números mais amplos dos complexos.

Formulários

O nome dos números imaginários foi proposto pelo matemático francês René Descartes (1596-1650) como uma zombaria ou desacordo com a proposta deles feita pelo matemático italiano do Raffaelle Century Bombelli.

Outros grandes matemáticos, como Euler e Leibniz, apoiaram Descartes nesse desacordo e chamados de números imaginários como Números anfíbios, que foram debatidos entre ser e nada.

O nome dos números imaginários é mantido hoje, mas sua existência e importância são muito reais e palpáveis, pois eles aparecem naturalmente em muitos campos de física, como:

-A teoria da relatividade.

-Em eletromagnetismo.

-Mecânica quântica.

Exercícios com números imaginários

- Exercício 1

Encontre as soluções da seguinte equação:

z² + 16 = 0

Solução

z² = -16

Tomando raiz quadrada nos dois membros que você tem:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Em outras palavras, as soluções da equação original são:

z = +4i ou z = -4i.

- Exercício 2

Encontre o resultado de aumentar a unidade imaginária para alimentar 5 menos subtração a unidade imaginária elevada à potência -5.

Solução

Yo⁵ - Yo-⁵ = i⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Exercício 3

Encontre o resultado da seguinte operação:

(3i)³ + 9i 

Solução

3³ Yo³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Exercício 4

Encontre as soluções da seguinte equação quadrática:

Pode atendê -lo: Teorema da existência e exclusividade: demonstração, exemplos e exercícios

(-2x)² + 2 = 0

Solução

A equação é reorganizada da seguinte maneira:

(-2x)² = -2

Em seguida, pegue uma raiz quadrada nos dois membros

√ (-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Então X é finalmente obtido:

x = ± √2 / 2 i

Ou seja, existem duas soluções possíveis:

x = (√2 / 2) i

Ou este outro:

x = - (√2 / 2) I

- Exercício 5

Encontre o valor de z definido por:

Z = √ (-9) √ (-4) + 7

Solução

Sabemos que a raiz quadrada de um número real negativo é um número imaginário, por exemplo √ (-9) é igual a √ (9) x √ (-1) = 3i.

Por outro lado, √ (-4) é igual a √ (4) x √ (-1) = 2i.

Para que a equação original possa ser substituída por:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Exercício 6

Encontre o valor de z resultante da seguinte divisão de dois números complexos:

Z = (9 - I²) / (3 + i)

Solução

O numerador de expressão pode levar em consideração a seguinte propriedade:

Uma diferença de quadrados é o produto da soma pela diferença dos binômios sem levantar o quadrado.

Então:

Z = [(3 - i) (3 + i)] / (3 + i)

A expressão resultante é então simplificada pelo restante

Z = (3 - i)

Referências

1. Earl, r. Números complexos. Recuperado de: matemática.boi.AC.Reino Unido.
2. Figuera, j. 2000. Matemática 1ª. Diversificado. Edições Co-Bo.
3. Hoffmann, J. 2005. Seleção de questões de matemática. Monfort Publications.
4. Jiménez, r. 2008. Álgebra. Prentice Hall.
5. Wikipedia. Número imaginário. Recuperado de: em.Wikipedia.org