Número de coordenação O que é, cálculo, exemplos

Ele Número de coordenação É a quantidade de átomos, íons ou moléculas que interagem com um centro em compostos de íons e coordenação. Esse conceito também pode ser aplicado às moléculas, levando em consideração quantos átomos estão ligados um ao outro em vez do número de seus links.

Esse número é importante porque define as geometrias dos complexos, as densidades de suas fases materiais e até o caráter estereoquímico (espacial) de suas reatividades. Para simplificar sua definição, eles são considerados vizinhos em todo átomo que envolve um centro específico.

Em uma área de moedas, podemos apreciar o que se entende por número de coordenação

Considere, por exemplo, o piso composto por moedas de imagem superior. Todas as moedas têm o mesmo tamanho e, se cada uma for observada, é cercada por seis outros; isto é, eles têm seis vizinhos e, portanto, o número de coordenação (c.N.) Para as moedas é 6. Essa mesma ideia agora se estende ao espaço tridimensional.

Se seus rádios forem desiguais, nem todos terão o mesmo número de coordenação. Por exemplo: quanto maior a moeda, mais vizinhos será capaz de interagir com um número maior de moedas ao redor. O oposto acontece com pequenas moedas.

[TOC]

Conceito do número de coordenação

Vs rádios de íons. Número de coordenação

O número de coordenação é o número de vizinhos mais próximos e que, em princípio, interagem diretamente com um centro, que é principalmente um íon metálico. Então, deixamos de lado as moedas para considerar as esferas.

Este íon metálico mⁿ⁺, onde n É igual ao seu número de oxidação ou Valência, interage com outros vizinhos (Ionic ou Molecular) chamados ligantes. Quanto maior n (+2, +3, etc.), menor será Mⁿ⁺ E, consequentemente, os ligantes serão forçados a se aproximar mais para interagir com Mⁿ⁺.

Pode servir a você: gordura butírica: obtenção, tipos, composição, usos, benefícios

A imagem a seguir ilustra o acima:

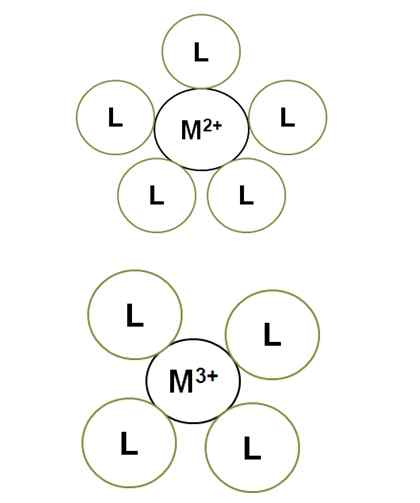Variação do número de coordenação com a carga central de íons. Fonte: Gabriel Bolívar.

M²⁺ No complexo iluminado, ele tem um número de coordenação de 5: é cercado por 5 ligantes l. Enquanto isso, m³⁺ tem um número de 4 coordenação. Isso é porque M³⁺, Para ter uma magnitude maior de carga, seu raio se contrai e, portanto, os ligantes devem se aproximar mais, o que aumenta suas repulsões eletrônicas.

É por isso que íons centrais volumosos, como os pertencentes a bloquear metais F, ou para o segundo ou terceiro período do bloco d, Eles tendem a ter números de coordenação mais altos (c.N. > 6).

Densidades

Suponha agora que o complexo M³⁺ sofre pressão. Chegará um ponto onde a pressão será tal que outro link é provável coordenado ou interagir com M³⁺. Isto é, seu número de coordenação aumentará de 4 para 5.

Em geral, as pressões aumentam o número de coordenação, à medida que os vizinhos se forçam no íon ou átomo central. Consequentemente, as fases materiais dessas substâncias se tornam mais densas, mais compactas.

Geometrias

Ilustrações superiores não dizem nada sobre geometrias em torno de M²⁺ ou m³⁺. No entanto, sabemos que um quadrado tem quatro vértices ou cantos, como um tetraedro.

Esse raciocínio conclui que a geometria em torno de M³⁺, cujo c.N. É 4, deve ser tetraédrico ou quadrado. Mas qual dos dois? Enquanto isso, geometrias para M²⁺, cujo c.N. É 5, eles podem ser uma pirâmide quadrada ou bipiramidal trigonal.

Cada c.N. Ele associou várias geometrias possíveis, que posicionam os ligantes a uma distância favorável, para que haja a menor repulsa entre eles.

Pode atendê -lo: links interatômicos

Como o número de coordenação é calculado ou determinado?

O número de coordenação pode ser calculado, às vezes, diretamente da fórmula composta em questão. Suponha que o complexo aniônico [Ni (CN)₅]^3-. Qual é o número de coordenação do íon níquel, ou²⁺? Basta observar o coeficiente estequiométrico 5, o que indica que existem 5 ânions CN^- coordenado ou interagindo com o centro de Ni²⁺.

No entanto, nem sempre é fácil. Por exemplo, o composto CUCN parece ter um número de coordenação de 1 ambos para Cu²⁺ Quanto ao CN^-. No entanto, consiste em realmente cadeias poliméricas Cu-CN-Cu-CN, então o número de coordenação correto é 2.

É por isso que o número de coordenação é preferível para determinar em vez de calcular. Como? Determinar as estruturas iônicas ou moleculares dos compostos. Isso é possível graças a técnicas instrumentais, como difração de raio -x, nêutrons ou elétrons.

Exemplos de números de coordenação

Em seguida e finalmente, alguns exemplos de compostos serão mencionados para cada um dos números de coordenação mais comuns. Da mesma forma, será dito quais são suas respectivas geometrias.

C.N. 2

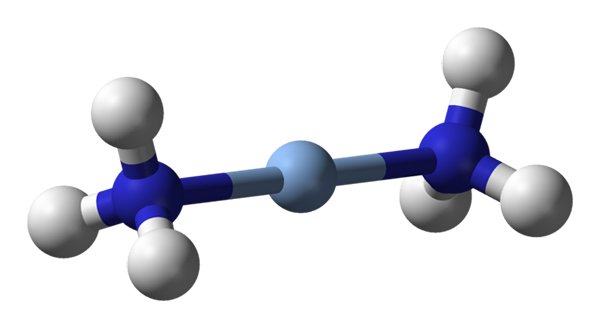Aqui a geometria linear de [Ag (NH3) 2] é observada+. Fonte: Benjah-BMM27 / Domínio Público

A c.N. igual a 2 significa que o átomo ou íons central tem apenas dois vizinhos. Portanto, conversamos sobre compostos obrigativamente sobre geometrias lineares. Entre eles, temos:

-HG (cap₃)₂

-[AG (NH₃)₂]⁺

-Ph₃Paucl

C.N. 3

Cada átomo de carbono nesta folha de grafite está conectado a outros três, por isso tem três vizinhos. Fonte: Benjah-BMM27 / Domínio Público

A c.N. igual a 3 significa que o átomo ou íon central é cercado por três vizinhos. Temos então geometrias como: plano trigonal (triangular), pirâmide trigonal e t de T. Exemplos de compostos com este número de coordenação são:

Pode atendê -lo: massa atômica: definição, tipos, como calculá -lo, exemplos

-[Cu (CN)₃]^2-

-[Pt (pcy₃)₃], Onde Pcy se refere ao ligante tricylohexylofospina

-Grafite

C.N. 4

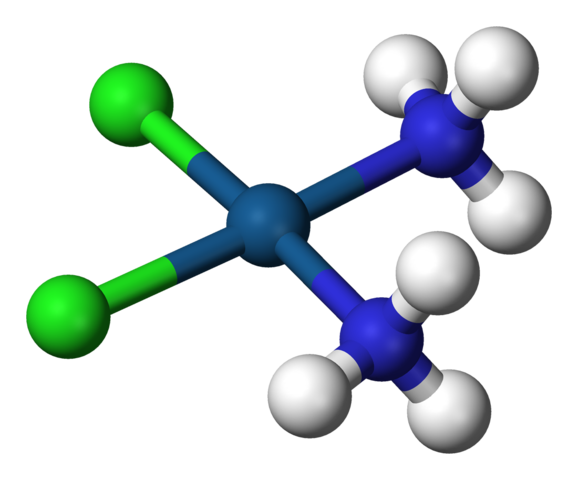Geometria quadrada da cisplatina, CIS-PTCL2 (NH3) 2. Fonte: Benjah-BMM27 / Domínio Público

A c.N. igual a 4 significa que o átomo ou íon central é cercado por quatro vizinhos. Suas geometrias possíveis são tetraédricas ou quadrados. Exemplos de compostos com este número de coordenação têm o seguinte:

-CH₄

-Cocl₂pyr₂

-CIS-PTCL₂(NH₃)₂

-[Alcl₄]^-

-[Moo₄]^2-

-SNCl₄

-[Cro₄]^2-

-[Mno₄]^2-

Todos esses exemplos, com exceção do CIS-PTCL₂(NH₃)₂, São geometrias tetraédricas.

C.N. 5

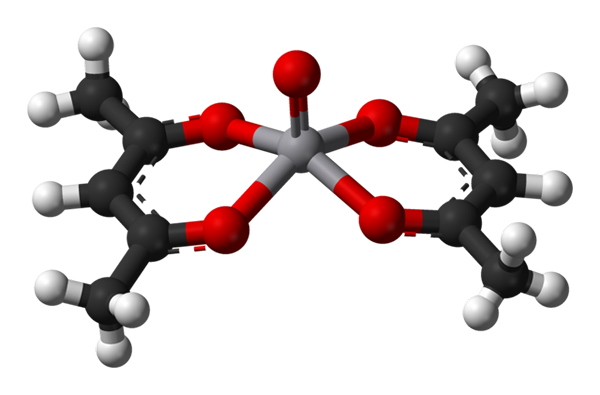Geometria de pirâmide quadrada para VO (ACAC) 2. Fonte: Benjah-BMM27 / Domínio Público.

A c.N. igual a 5 significa que o átomo ou íons central é coordenado ou interagido com cinco vizinhos. Suas geometrias, já mencionadas, são a pirâmide quadrada ou bipiramidal trigonal. Como exemplos, temos o seguinte:

-[Cobrn (CH₂CH₂NME₂)₃]

-[Fe (CO)₅]

-VO (ACAC)₂, ACAC sendo o ligante de acetilacetonato

C.N. 6

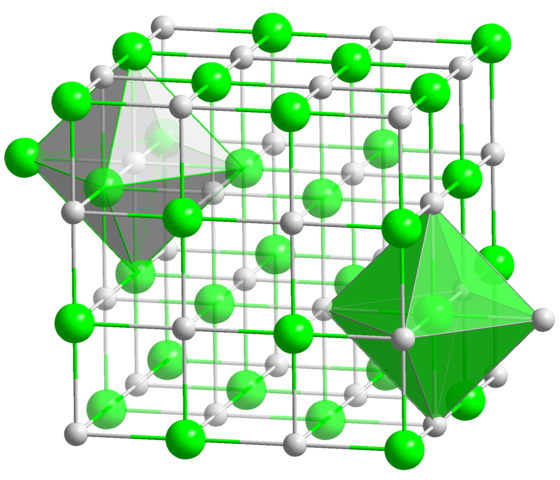Na estrutura cristalina do NaCl, cada íon Na+ e Cl- tem seis vizinhos, então esse é o número de coordenação para ambos os íons (ver o octaedro). Fonte: Estado sólido / domínio público

Este é, de longe, o número de coordenação mais comum entre todos os compostos. Lembre -se do exemplo das moedas principais. Mas em vez de sua geometria favorita é a de um hexágono plano, corresponde ao do octaedro (normal ou distorcido), além do prisma trigonal. Alguns dos muitos exemplos de compostos com este número de coordenação são:

-[Alf₆]^3-

-[CO (NH₃)₆]³⁺

-[ZR (escolha₃)₆]^2-

-NaCl (sim, sal de mesa)

-Mos₂, Observe que c.N. Pois este composto não é 2

Outros

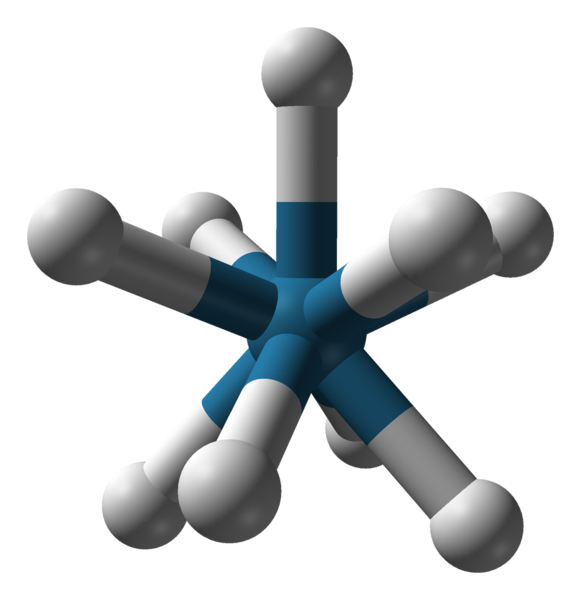Geometria do ânion triapádico do ânion [Reh9] 2-. Fonte: Benjah-BMM27 / Domínio Público.

Existem outros números de coordenação, de 7 a 15. Para que c.N. Seja alto, o íon ou átomo central deve ser muito grande, ter pouca carga e, ao mesmo tempo, os ligantes devem ser muito pequenos. Alguns exemplos de compostos com esse c.N. Eles estão abaixo e terminarem:

-K₃[NBOF₆], C.N. 7 e geometria octaedro

-[MO (CN)₈]^3-

-[ZR (Ox)₄]^2-, sendo boi o ligante oxalato

-[Reh₉]^2-

-[Franca₃)₆]^2-, C.N. igual a 12

Referências

1. Whitten, Davis, Peck e Stanley. (2008). Química. (8ª ed.). Cengage Learning.
2. Shiver & Atkins. (2008). Química Inorgânica. (Quarta edição). Mc Graw Hill.
3. Wikipedia. (2020). Número de coordenação. Recuperado de: em.Wikipedia.org
4. Os editores da Enyclopaedia Britannica. (s.F.). Número de coordenação. Recuperado de: Britannica.com
5. Prof. Robert J. Lancashire. (15 de agosto de 2020). Números de coordenação e geometria. Química Librettexts. Recuperado de: química.Librettexts.org
6. Helmestine, Anne Marie, Ph.D. (28 de agosto de 2020). Definição de número de coordenação em química. Recuperado de: pensamento.com