Exemplos de ângulos conjugados internos e externos, exercícios

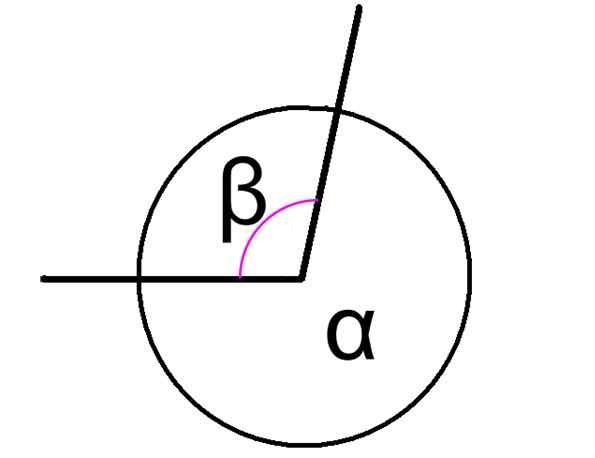
O ângulos conjugados Eles são os que são adicionados como resultado de 360 ​​°, independentemente de esses ângulos serem adjacentes ou não. A Figura 1 mostra dois ângulos conjugados, indicados como α e β.

Nesse caso, os ângulos α e β da figura têm um vértice comum e seus lados são comuns, portanto são adjacentes. A relação entre eles é expressa da seguinte maneira:

α + β = 360º

figura 1. Dois ângulos centrais conjugados, soma. Fonte: Wikimedia Commons. Nenhum autor legível por máquina fornecido. Thiago R Ramos assumiu (com base em reivindicações de direitos autorais). [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/)] é uma classificação dos ângulos por sua soma. Outras definições importantes incluem ângulos complementares, cuja soma é 90 º e o ângulos suplementares, que totaliza 180 º.

Por outro lado, vamos agora considerar duas linhas paralelas cortadas por um secante, cuja disposição é mostrada então:

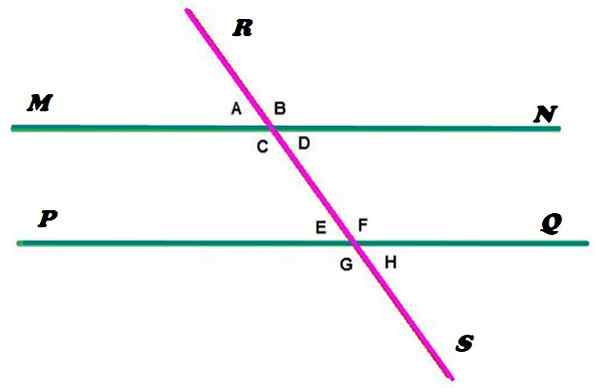Figura 2. Linhas paralelas cortadas por um secante. Fonte: f. Zapata.

As linhas Mn e PQ são paralelas, enquanto a linha RS está secando, cruzando paralelos em dois pontos. Como pode ser visto, essa configuração determina a formação de 8 ângulos, aos quais foi indicado com pequenas letras.

Bem, de acordo com a definição dada no início, os ângulos A, B, C e D são conjugados. E da mesma maneira que são E, F, G e H, pois ambos os casos são cumpridos que:

A+b+c+d = 360º

E

E+f+g+h = 360º

Para esta configuração, dois ângulos são conjugados se estiverem do mesmo lado em relação à linha de secagem RS e ambos são internos ou externos. No primeiro caso, há falar de ângulos Conjugados internos, Enquanto estão no segundo, eles são ângulos conjugado externo.

[TOC]

Exemplos

Na Figura 2, os ângulos externos são aqueles que estão fora da região delimitados pelas linhas Mn e PQ, são os ângulos A, B, G e H. Enquanto os ângulos que estão entre as duas linhas são C, D, E e F.

Pode servir a você: coplanares pontos: equação, exemplo e exercícios resolvidos

Agora é necessário analisar quais ângulos estão à esquerda e que à direita do secante.

À esquerda de Rs estão os ângulos A, C, E e G. E à direita estão B, D, F e H.

Passamos imediatamente a determinar os casais de ângulos conjugados, de acordo com a definição dada na seção anterior:

-A e G, externo e à esquerda de Rs.

-D e F, interno e à direita de Rs.

-B e H, externo e à direita de Rs.

-C e E, interno e à esquerda de Rs.

Propriedade de ângulos conjugados entre linhas paralelas

Os ângulos conjugados entre linhas paralelas são suplementares, ou seja, sua soma é igual a 180 °. Dessa forma, para a Figura 2, o seguinte é cumprido:

A + g = 180º

D + f = 180º

B + h = 180º

C + E = 180º

Os pares de ângulos correspondentes para linhas paralelas

Eles são aqueles que estão do mesmo lado da linha de secagem, não são adjacentes e um deles é interno e o outro é externo. É importante visualizá -los, pois sua medida é a mesma, porque eles são ângulos opostos pelo vértice.

Voltando à Figura 2, os ângulos correspondentes são identificados como:

-A e e

-C e g

-B e f

-D e h

Ângulos internos de um quadrilateral

Os quadrilásteros são polígonos de 4, incluindo o quadrado, o retângulo, o trapézio, o paralelogramo e o rombus, por exemplo, por exemplo. Independentemente de sua forma, em qualquer um deles, é cumprido que a soma de seus ângulos internos é 360º, portanto, eles estão em conformidade com a definição dada no começo.

Vejamos alguns exemplos de quadriláteros e como calcular o valor de seus ângulos internos de acordo com as informações das seções anteriores:

Pode atendê -lo: quais são os 7 elementos da circunferência?

Exemplos

a) Três dos ângulos de uma medida quadrilateral 75º, 110º e 70º. Quanto deve medir o ângulo restante?

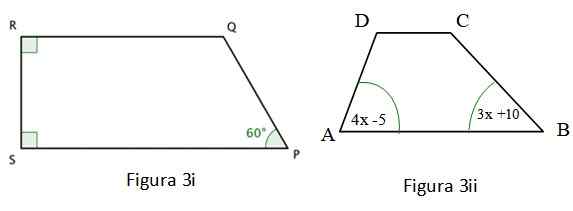
b) Encontre o valor do ângulo ero na Figura 3 i.

c) Calcule quanto mede o ângulo porte da Figura 3 ii.

Solução para

Seja α o ângulo que falta, é cumprido que:

α + 75 º + 110º + 70º = 360 → α = 105º

Solução b

A Figura 3i mostrada é um Trapézio E dois de seus ângulos internos são retos, que foram apontados com um quadrado de cores nos cantos. Para este quadrilateral, o seguinte é verificado:

r + porte + ero + eroQ = 360º; Porte = porte = 90º; p = 60º

Portanto:

Porte q = 2 x 90º + 60º = 240º

Solução c

O quadrilátero da Figura 3 II também é um trapézio, para o qual o seguinte é cumprido:

Ero + porteb + ero + porte = 360º

Portanto:

4x -5 + 3x + 10 +180 = 360

7x + 5 = 180

X = (180 - 5) / 7

x = 25

Para determinar o ângulo solicitado na declaração, é usado que ente = 4x - 5. Substituindo o valor de x calculado anteriormente, é seguido que ente = (4 × 25) -5 = 95º

Exercícios

- Exercício 1

Sabendo que um dos ângulos mostrados vale 125, encontrando as medidas dos 7 ângulos restantes na figura a seguir e justificando as respostas.

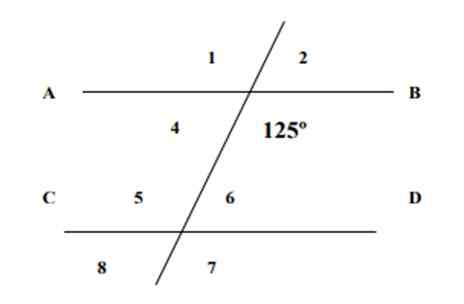Figura 4. As linhas e ângulos do Exercício 1. Fonte: f. Zapata.

Solução

O ângulo 6 e o ​​ângulo 125 são conjugados internos, cuja soma vale 180º, de acordo com a propriedade dos ângulos conjugados, portanto:

A6 + 125º = 180º → ¼6 = 180º - 125º = 55º

Por outro. Portanto ero 8 mede 55º.

Pode servir você: álgebra vetorial

O ângulo porte1 também é oposto pelo vértice em 125, então podemos afirmar que ϩ1 = 125º. Também podemos apelar para o fato de que os pares de ângulos correspondentes têm a mesma medida. Na figura, esses ângulos são:

Ϩ7 = 125 °

Ϩ2 = ero6 = 55 °

Amor1 = porte 5 = 125º

Ϩ4 = porte8 = 55 °

- Exercício 2

Encontre o valor de x na figura a seguir e os valores de todos os ângulos:

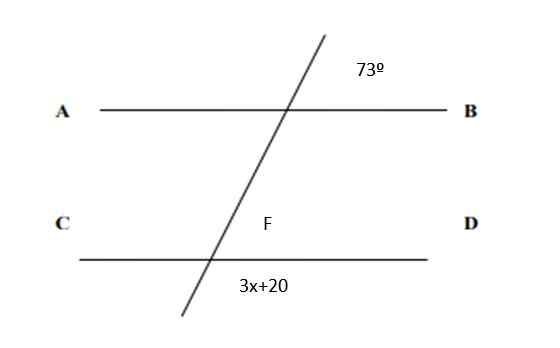Figura 5. Linhas e ângulos para o Exercício 2. Fonte: f. Zapata.

Solução

Como eles são pares correspondentes, segue -se que F = 73º. E por outro lado, a soma dos pares conjugados é de 180º, portanto:

3x + 20º + 73º = 180º

3x = 180º - 73º -20º = 87

Finalmente, o valor de x é:

x = 87/3 = 29

Quanto a todos os ângulos, eles aparecem listados na figura a seguir:

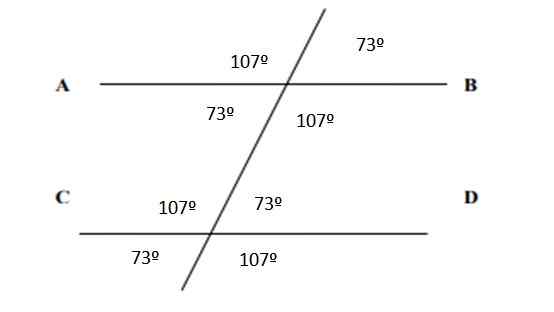Figura 6. Ângulos resultando no Exercício 2. Fonte: f. Zapata.

Referências

1. Grupos de ângulo. Ângulos complementares, suplementares e complementares. Recuperado de: thisiget.coma
2. Baldor, a. 1983. Geometria plana e espacial e trigonometria. Grupo de pátria cultural.
3. Corral, m. Mathematics Librettexts: ângulos. Recuperado de: matemática.Librettexts.org.
4. Mathmania. Classificar e construir ângulos por sua medição. Recuperado de: Mathemania.coma
5. Wentworth, G. Geometria do Planeta. Recuperado de: Gutenberg.org.
6. Wikipedia. Ângulos conjugados. Recuperado de: é.Wikipedia.org.