Coplanares Points equação, exemplo e exercícios resolvidos

O Pontos de coplanares Todos pertencem ao mesmo avião. Dois pontos são sempre coplanares, pois esses pontos definem uma linha através da qual os infinitos planos passam. Então, ambos os pontos pertencem a cada um dos planos que passam pela linha e, portanto, sempre serão coplanares.

Por outro.

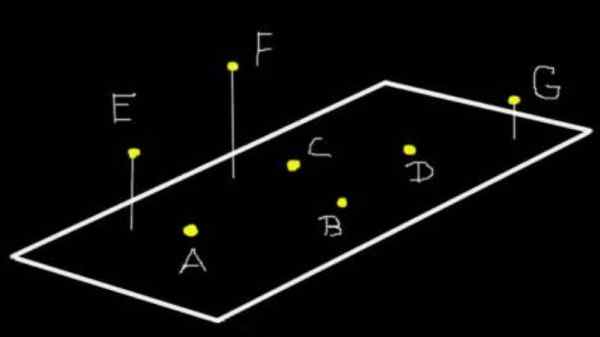
figura 1. A, B, C e D são coplanares para o avião (ω). E, f e g não são coplanares a (ω), mas se forem coplanares para o avião que três definem. Fonte: f. Zapata.

Mais de três pontos podem ser coplanares ou não. Por exemplo, na Figura 1, os pontos A, B, C e D são coplanares para o avião (ω). Mas e, f e g não são coplanares a (ω), embora sejam coplanares para o avião que três definem.

[TOC]

Equação de um avião com três pontos

A equação de um plano determinado por três pontos conhecidos a, b, c é uma relação matemática que garante que qualquer ponto p de coordenadas genéricas (x, y, z) que cumpre a equação pertence ao referido plano. 

A declaração anterior é equivalente a dizer que, se p de coordenada (x, y, z) atingir a equação plana, então o ponto será copatar com os três pontos a, b, c que determinaram o plano.

Para encontrar a equação do referido avião, vamos começar encontrando os vetores Ab e AC:

Ab = [Bx - ax, por - ay, bz - az]

AC = [Cx - ax, cy - ay, cz - az]

O produto vetorial Ab X AC Isso resulta em um vetor perpendicular ou normal ao plano determinado pelos pontos a, b, c.

Um ponto de coordenadas (x, y, z) pertence ao avião se for verdade que o vetor AP é perpendicular ao vetor Ab X AC, que é garantido se cumprido:

Pode servir a você: Decágono: regular, irregular, propriedades, exemplos

AP • (AB X AC) = 0

Isso é equivalente a dizer que o produto triplo de AP, Ab e AC Seja nulo. A equação anterior pode ser escrita de maneira matricial:

Exemplo

Deixe os pontos a (0, 1, 2); B (1, 2, 3); C (7, 2, 1) e D (para, 0, 1). Que valor deve ter para para que os quatro pontos sejam coplanares?

Solução

Para encontrar o valor de A, é necessário que o ponto d faça parte do plano determinado por A, B e C, que é garantido se a equação plana encontrar.

Desenvolvendo o determinante que temos:

A (-1-1) + 1 (-1 -7) -1 (1 -7) = -2a -8 + 6 = -2a -2 = 0

A equação anterior indica que A = -1 Para cumprir a igualdade. Em outras palavras, a única maneira que o ponto d (para, 0.1) seja coplanar com os pontos A, B e C é que para Valga -1. Caso contrário, não será coplanar.

Exercícios resolvidos

- Exercício 1

Um avião cruza os eixos cartesianos x, y, z em 1, 2 e 3, respectivamente. A interseção do referido plano com os eixos determina os pontos A, B e C. Encontre o componente DZ de um ponto D, cujos componentes cartesianos são:

 D (-dz, dz+1, dz) 

Sob condição de que D é coplanar com pontos A, B e C. 

Solução

Quando as interceptações de um avião com os eixos cartesianos são conhecidos, a forma segmentar da equação plana pode ser usada:

x/1 + y/2 + z/3 = 1

Como o ponto D deve pertencer ao avião anterior, você deve::

-Dz/1 + (dz + 1)/2 + dz/3 = 1

Quer dizer:

-Dz + dz/2 + ½ + dz/3 = 1

Dz (-1 + ½ + ⅓) = ½ 

Dz (-1/6⅙) = ½ 

Dz = -3 

A partir do exposto, segue -se que o ponto d (3, -2, -3) deve se acoplar com os pontos a (1, 0, 0); B (0, 2, 0) e C (0, 0, 3).

Pode atendê -lo: critérios de similaridade triangulosa

- Exercício 2

Determinar se os pontos a (0, 5, 3); B (0, 6, 4); C (2, 4, 2) e D (2, 3, 1) são coplanares.

Solução

Formamos a matriz cujas fileiras são as coordenadas de D-A, B-A e C-A. Então o determinante é calculado e é verificado se zero ou não.

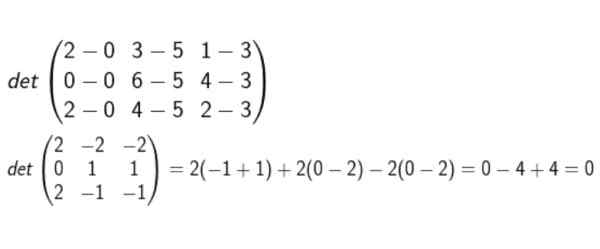
Depois de realizar todos os cálculos, conclui -se que eles são coplanares.

- Exercício 3

Duas linhas são dadas no espaço. Um deles é a linha (r) cuja equação paramétrica é:

(R): x = 1 + 2 λ; y = 1 - λ; Z = 1

E o outro é a (s) linha (s) cuja equação é:

(S): x + 2 y = 1; Z = -1

Demonstrar que (r) e (s) eles são coplanários retos, ou seja, eles estão no mesmo plano.

Solução

Vamos começar arbitrariamente dois pontos na linha (r) e dois na (s) linha (s):

Reto (r): λ = 0; A (1, 1, 1) e λ = 1; B (3, 0, 1)

Vamos fazer x = 0 na (s) linha (s)=> y = ½; C (0, ½, -1). E por outro lado, se o fizermos y = 0 => x = 1; D (1, 0, -1).

Ou seja, levamos os pontos A e B que pertencem à linha (R) e aos pontos C e D que pertencem à (s) linha (s). Se esses pontos forem coplanares, as duas linhas também serão.

Agora escolhemos apontar como o pivô e depois encontramos as coordenadas dos vetores Ab, AC e DE ANÚNCIOS. Dessa forma, você recebe:

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -A: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

D -a: (1-1, 0 -1, -1 -1) => DE ANÚNCIOS= (0, -1, -2)

O próximo passo é construir e calcular o determinante cuja primeira linha é os coeficientes vetoriais Ab, A segunda fila são os de AC e a terceira fila dos do vetor DE ANÚNCIOS:

Pode atendê -lo: Miletus como o teorema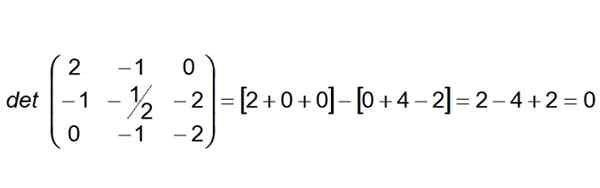

Como o determinante acaba sendo nulo, podemos concluir que os quatro pontos são coplanarios. Além disso, pode -se dizer que as linhas (r) e (s) também são coplanares.

- Exercício 4

As linhas (r) e (s) são coplanares, como demonstrado no Exercício 3. Encontre a equação do avião que os contém.

Solução

Pontos A, B, C definem completamente esse plano, mas queremos impor que qualquer ponto x de coordenadas (x, y, z) pertencem ao mesmo.

X - a: (x -1, y -1, z - 1) => Machado= (X -1, y -1, z -1)

B - A: (3-1, 0 -1, 1 - 1) => Ab= (2, -1, 0)

C -A: (0-1, 1/2 -1, -1 -1) => AC= (-1, -1/2, -2)

De modo que X pertence ao plano definido por A, B, C e em que as linhas (R) e (S) estão contidas, é necessário que o determinante formado em sua primeira linha seja anulado pelos componentes de Machado, no segundo por aqueles Ab E no terceiro por aqueles AC:

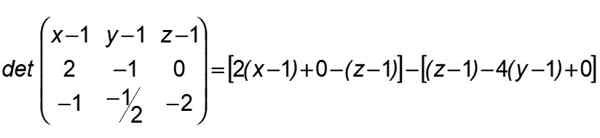
Após esse resultado, agrupamos dessa maneira:

2 (x-1) + 4 (y-1) -2 (z-1) = 0

E imediatamente é visto que pode ser reescrito assim:

x - 1 + 2y - 2 - z + 1 = 0

Portanto, x + 2y - z = 2 é a equação do plano que contém as linhas (r) e (s).

Referências

1. Fleming, w. 1989. Matemática do Pré -Eleno. Prentice Hall Ptr.
2. Kolman, b. 2006. Álgebra Linear. Pearson Education.
3. Leal, j. M. 2005. Geometria analítica plana. Mérida - Venezuela: editorial venezuelano C. PARA.
4. Navarro, Rocio. Os vetores. Recuperado de: livros.Google.co.ir.
5. Pérez, c. D. 2006. Pré -cálculo. Pearson Education.
6. PreNowitz, w. 2012. Conceitos básicos de geometria. Rowman & Littlefield.
7. Sullivan, m. 1997. Pré -cálculo. Pearson Education.