Medidas de posição, tendência central e dispersão

As medidas de tendência central, dispersão e posição, Estes são os valores usados ​​para interpretar adequadamente um conjunto de dados estatísticos. Estes podem ser trabalhados diretamente, conforme obtido do estudo estatístico, ou podem ser organizados em grupos de igual frequência, facilitando a análise.

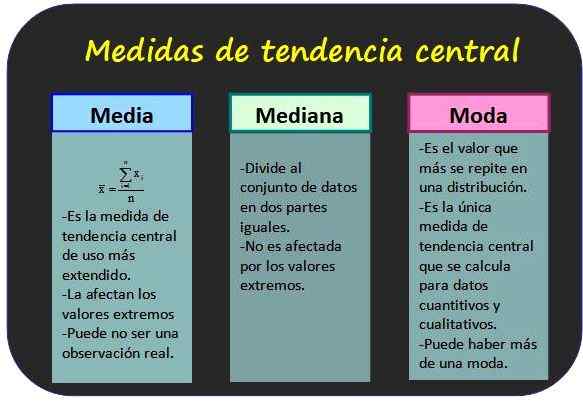
As três medidas de tendência central mais conhecidas e algumas de suas propriedades. Fonte: f. Zapata.

Medidas de tendência central

Eles permitem saber sobre quais valores os dados estatísticos são agrupados.

Média aritmética

Também é conhecido como a média dos valores de uma variável e é obtido adicionando todos os valores e dividindo o resultado pelo número total de dados.

• Média aritmética para dados sem agrupar

Seja uma variável X da qual não há dados sem organizar ou agrupar, sua média aritmética é calculada da seguinte forma:

E em notação sumária:

Exemplo

Os proprietários de um albergue de turistas da montanha pretendem saber quantos dias, em média, os visitantes permanecem nas instalações. Para fazer isso, foi realizado um registro dos dias de permanência de 20 grupos de turistas, obtendo os seguintes dados:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

Os dias médios em que os turistas ficam é:

= 2.5 dias

• Média aritmética para dados agrupados

Se os dados variáveis ​​estiverem organizados em uma tabela de frequência absoluta f_Yo E os centros de classe são x₁, x₂,…, X_n, A média é calculada por:

No resumo do verão:

Mediana

A mediana de um grupo de n valores de variável x é o valor central do grupo, desde que os valores sejam cada vez mais ordenados. Dessa forma, metade de todos os valores é menor que a moda e a outra metade é maior.

• Meio de dados não agrupados

Os seguintes casos podem ser apresentados:

-Número N Valores da variável x  chance: A mediana é o valor que está apenas no meio do grupo de valores:

-Número N Valores da variável x par: Nesse caso, a mediana é calculada como a média dos dois valores centrais do grupo de dados:

Exemplo

Para encontrar a mediana dos dados do albergue turístico, eles são ordenados pela primeira vez do menos para o maior:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Pode atendê -lo: qual é a frequência relativa e como é calculada?

O número de dados é par, portanto, existem dois dados centrais: x₁₀ e x_onze E como ambos valem 2, sua média também.

Mediana = 2

• Médio de dados agrupados

A fórmula a seguir é usada:

Os símbolos na fórmula significam:

-C: largura de intervalo contendo mediana

-B_M: borda inferior desse mesmo intervalo

-F_m: Número de observações contendo o intervalo ao qual a mediana pertence.

-N: Dados totais.

-F_BM: número de observações antes do intervalo que contém a mediana.

Moda

A moda para dados não agrupados é o valor mais freqüente, enquanto para os dados agrupados, é a classe mais freqüente. É considerado moda como os dados mais representativos ou classe de distribuição.

Duas características importantes dessa medida são que um conjunto de dados pode ter mais de uma moda, e a moda pode ser determinada para dados quantitativos e dados qualitativos.

Exemplo

Continuando com os dados do albergue turístico, o que mais se repetiu é 1, portanto, a coisa mais comum é que os turistas permanecem 1 dia no albergue.

Medidas de dispersão

As medidas de dispersão descrevem como os dados agrupados em torno das medidas centrais são.

Faixa

É calculado subtraindo os dados principais e os dados menores. Se essa diferença for grande, é um sinal de que os dados são dispersos, enquanto os pequenos valores indicam que os dados estão próximos da média.

Exemplo

O intervalo para os dados do Hostel turístico é:

Intervalo = 5−1 = 4

Variação

• Variação para dados não agrupados

Para encontrar a variação s² É necessário primeiro conhecer a média aritmética, então a diferença é calculada no quadrado entre cada dados e a média, todos são adicionados e divididos pelo total de observações. Essas diferenças são conhecidas como desvios.

A variação, que é sempre positiva (ou zero), indica até que ponto as observações da média: se a variação for alta, os valores são mais dispersos do que quando a variação é pequena.

Exemplo

A variação para os dados do albergue turístico é:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Variação para dados agrupados

Para encontrar a variação de um grupo de dados agrupados, eles são necessários: i) a média, ii) a frequência f_Yo  que é o total de dados em cada classe e iii) x_Yo  ou valor de classe:

Pode atendê -lo: tipos de triângulos

Desvio padrão

La desviación estándar es la raíz cuadrada positiva de la varianza, por lo que tiene una ventaja sobre la varianza: viene en las mismas unidades que la variable bajo estudio y así se tiene una idea más directa de lo cerca o lejos que está la variable de a média.

• Desvio padrão para dados não agrupados

É determinado simplesmente encontrando a raiz quadrada da variação para dados não cortados:

 Exemplo

O desvio padrão para dados de albergues turísticos é:

S = √ (s²) = √1.95 = 1.40

• Desvio padrão para dados agrupados

É calculado encontrando a raiz quadrada da variação para dados agrupados:

Medidas de posição

Medidas de posição Divida um conjunto ordenado de dados em partes iguais. A mediana, além de ser uma medida de tendência central, também é uma medida de posição, pois divide o todo em duas partes iguais. Mas você pode obter peças menores com quartis, deciles e percentis.

Quartis

Quartiles dividem o conjunto em quatro partes iguais, cada uma com 25 % dos dados. Eles são denotados como q₁, Q₂ e que₃ E a mediana é o quartil q₂. Dessa forma, 25% dos dados estão abaixo do quartil q₁, 50% abaixo do quartil q₂ ou mediana e 75% sob o quartil q₃.

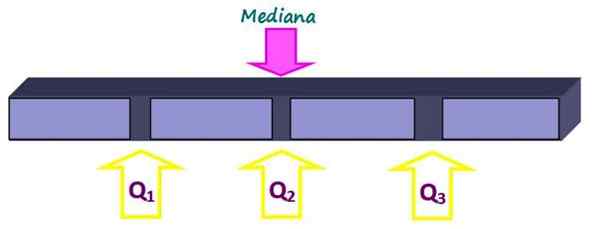Figura 2. Quartiles dividem o conjunto de dados em quatro partes iguais. Fonte: f. Zapata.

• Quartis para dados não agrupados

Os dados são ordenados e o total é dividido em 4 grupos com o mesmo número de dados cada. A posição do primeiro quartil é encontrada por:

Q₁ = (n+1)/4

Sendo o total de dados. Se o resultado são os dados inteiros correspondentes a essa posição, mas se for decimal, os dados correspondentes a toda a parte com o seguinte serão calculados em média ou, para maior precisão, é linearmente interpolado entre os dados referidos.

Exemplo

A posição do primeiro quartil q₁ Para os dados do albergue turístico é:

Q₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Esta é a posição do quartil 1 e, como o resultado é decimal, os dados X são procurados₅ e x_6, que são respectivamente x₅ = 1 e x₆ = 1 e eles são calculados, resultantes:

Primeiro Quartil = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

A posição do segundo quartil q₂ é:

Pode atendê -lo: Soma telescópica: como é resolvido e resolvido exercícios

Q₂ = 2 (n+1)/4 = 10.5

Qual é a média entre x₁₀ e x_onze e coincide com a mediana:

Segundo quartil = mediana = 2

A terceira posição de quartil é calculada por:

Q₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Também é decimal, portanto x é calculado_quinze e x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Mas como ambos valem 4:

Terceiro Quartil = 4

A fórmula geral para a posição dos quartis em dados não cheios é:

Q_k = K (n+1)/4

Com k = 1,2,3.

• Quartis para dados agrupados

Eles são calculados semelhantes à mediana:

A explicação dos símbolos é:

-B_Q: borda inferior do intervalo contendo quartil

-C: Largura desse intervalo

-F_q: Número de observações continham o intervalo de quartil.

-N: Dados totais.

-F_BQ: Número de dados antes do intervalo contendo quartil.

Deciles e percentis

Decis e percentis dividem o conjunto de dados em 10 partes iguais e 100 partes iguais, respectivamente, e seu cálculo é realizado análogo ao dos quartis.

• Decis e percentis para dados não agrupados

As fórmulas são usadas respectivamente:

D_k = K (n+1)/10

Com k = 1,2,3… 9.

Decil d₅ Deve ser igual à mediana.

P_k = K (n+1)/100

Com k = 1,2,3… 99.

O percentil p_cinquenta Deve ser igual à mediana.

Exemplo

No exemplo do albergue turístico, a posição do D₃ é:

D₃ = 3 (20+1)/10 = 6.3

Como um número decimal é média x₆ e x_7, ambos iguais a 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Significa que 3 décimos dos dados estão abaixo de x₇ = 1 e o restante acima.

• Deciles e percentis para dados agrupados

As fórmulas são análogas às de quartis. D é usado para denotar os deciles e P para os percentis e os símbolos são interpretados de maneira semelhante:

A regra empírica

Quando os dados são distribuídos simetricamente e a distribuição é unimodal, há uma regra chamada  Regra empírica qualquer Regra 68 - 95 - 99, Isso os agrupa nos seguintes intervalos:

• 68% dos dados estão no intervalo:

• 95% dos dados estão no intervalo:

• 99% dos dados estão no intervalo:

Exemplo

Em que intervalo é 95% dos dados do albergue turístico?

Eles estão no intervalo: [2.5−1.40; 2.5+1.40] = [1.1; 3.9].

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
3. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
4. Spiegel, m. 2009. Estatisticas. Série Schaum. 4 ta. Edição. McGraw Hill.
5. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.