Fórmulas de coeficiente de determinação, cálculo, interpretação, exemplos

Ele Coeficiente de determinação É um número entre 0 e 1 que representa a fração de pontos (x, y) que seguem a linha de ajuste por regressão de um conjunto de dados com duas variáveis.

Também é conhecido como ajuste bondade e é denotado por R². Para calculá -lo, o quociente é obtido entre a variação dos dados ŷi estimados pelo modelo de regressão e a variação dos dados Yi correspondentes a cada xi dos dados.

R² = Sŷ / sy

figura 1. Coeficiente de correlação para quatro pares de dados. Fonte: f. Zapata.

Se 100% dos dados estiverem na linha de função de regressão, o coeficiente de determinação será 1.

Pelo contrário, se para um conjunto de dados e uma determinada função de ajuste, o coeficiente R r² Acaba sendo igual a 0.5, então pode -se dizer que o ajuste é satisfatório ou bom a 50%. 

Da mesma forma, quando o modelo de regressão joga valores de r² menos de 0.5, isso indica que a função de ajuste escolhida não se adapta satisfatoriamente aos dados, portanto, é necessário procurar outra função de ajuste.

E quando covariância ou o coeficiente de correlação Tende a zero, então as variáveis ​​x e y dos dados não estão relacionadas e, portanto, r² também tenderá a zero.

[TOC]

Como calcular o coeficiente de determinação?

Na seção anterior, foi dito que o coeficiente de determinação é calculado encontrando o quociente entre as variações:

-Estimado pela função de regressão da variável e 

-A variável yi correspondente a cada uma das variáveis ​​xi. 

Na forma matemática, permanece assim:

R² = Sŷ / sy

A partir desta fórmula, segue -se que r² representa a proporção de variância explicada pelo modelo de regressão. Alternativamente, r pode ser calculado² Através da fórmula a seguir, totalmente equivalente ao anterior:

R² = 1 - (Sε / SY)

Onde Sε representa a variação dos resíduos εi = ŷi - yi, enquanto sy é a variação do conjunto de dados dos dados dos dados. Para determinar ŷi, a função de regressão é aplicada, o que significa afirmar que ŷi = f (xi).

Pode servir a você: Fração equivalente a 3/5 (solução e explicação)

A variação do conjunto de dados YI, com I de 1 a N é calculada dessa maneira:

Sy = [σ (yi -)² ) / (N-1)]

E depois prossiga de maneira semelhante para Sŷ ou para Sε.

Caso ilustrativo

Por meio de mostrar os detalhes da maneira como o cálculo do Coeficiente de determinação Vamos pegar o seguinte conjunto de quatro pares de dados: 

(X, y): (1, 1); (23); (3, 6) e (4, 7).

Um ajuste de regressão linear é proposto para este conjunto de dados obtido pelo método dos mínimos quadrados:

f (x) = 2.1 x - 1 

Aplicando esta função de ajuste, os pares são obtidos:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) e (4, 7.4).

Em seguida, calculamos a média aritmética para x e y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Variância sy

Sy = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Variação Sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Coeficiente de determinação r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Interpretação

O coeficiente de determinação para o caso ilustrativo considerado no segmento anterior acabou sendo 0.98. Ou seja, o ajuste linear através da função:

 f (x) = 2.1x - 1

É 98% confiável para explicar os dados com os quais foram obtidos através do método mínimo quadrado. 

Além do coeficiente de determinação, existe o Coeficiente de correlação linear ou também conhecido como coeficiente de Pearson. Este coeficiente, indicado como r, É calculado pelo seguinte relacionamento:

R = sxy / (sx sy)

Aqui, o numerador representa a covariância entre as variáveis ​​x e y, enquanto o denominador é o produto do desvio padrão da variável x e o desvio padrão para a variável e.

O coeficiente de Pearson pode levar valores entre -1 e +1. Quando esse coeficiente tende a +1, há correlação linear direta entre x e y. Se, em vez disso, tende a -1, há correlação linear, mas quando x cresce e diminui. Finalmente, está perto de 0, não há correlação entre as duas variáveis.

Pode atendê -lo: dados agrupados: exemplos e exercícios resolvidos

Deve -se notar que o coeficiente de determinação coincide com o quadrado do coeficiente de Pearson, somente quando o primeiro foi calculado com base em um ajuste linear, mas essa igualdade não é válida para outros ajustes não lineares.

Exemplos

- Exemplo 1

Um grupo de estudantes do ensino médio pretende determinar uma lei empírica para o período de um pêndulo em função de seu comprimento. Para atingir esse objetivo, eles fazem uma série de medições nas quais medem o tempo de uma oscilação do pêndulo para diferentes comprimentos, obtendo os seguintes valores:

Comprimento (m)	Período (s)
0.1	0,6
0,4	1.31
0,7	1.78
1	1.93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

É solicitado para fazer um gráfico de dispersão de dados e fazer um ajuste linear por regressão. Além disso, mostre a equação de regressão e seu coeficiente de determinação.

Solução

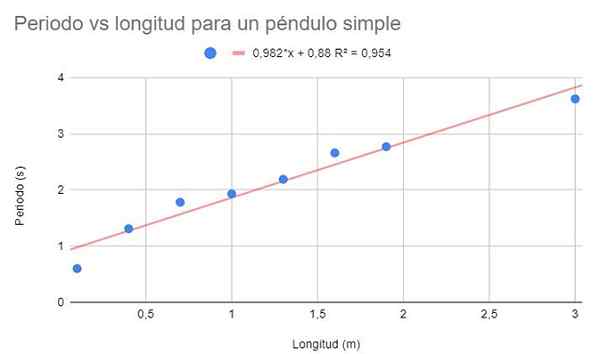Figura 2. Solução gráfica do Exercício 1. Fonte: f. Zapata.

Um coeficiente de determinação razoavelmente alto (95%) pode ser observado, portanto, pode -se pensar que o ajuste linear é ideal. No entanto, se os pontos forem observados juntos, parece que eles tendem a se curvar. Este detalhe não é contemplado no modelo linear.

- Exemplo 2

Para os mesmos dados do Exemplo 1, faça um gráfico de dispersão de dados. Nesta ocasião, diferentemente do Exemplo 1, é solicitado a fazer um ajuste de regressão através de uma função potencial.

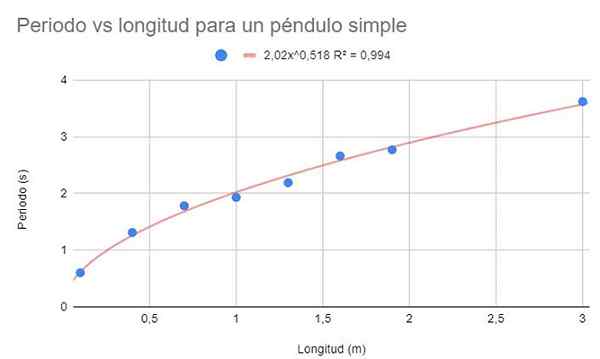Figura 3. Solução gráfica do exercício 2. Fonte: f. Zapata.

Mostram também a função de ajuste e seu coeficiente de determinação r².

Solução

A função potencial é da forma f (x) = ax^B, onde A e B são constantes que são determinados pelo método mínimo quadrado.

A figura anterior mostra a função potencial e seus parâmetros, bem como o coeficiente de determinação com um valor muito alto de 99%. Observe que os dados seguem a curvatura da linha de tendência.

Pode atendê -lo: princípio aditivo

- Exemplo 3

Com os mesmos dados do Exemplo 1 e Exemplo 2, faça um ajuste polinomial de segundo grau. Mostre o gráfico, o polinômio de ajuste e o coeficiente de determinação r² correspondente.

Solução

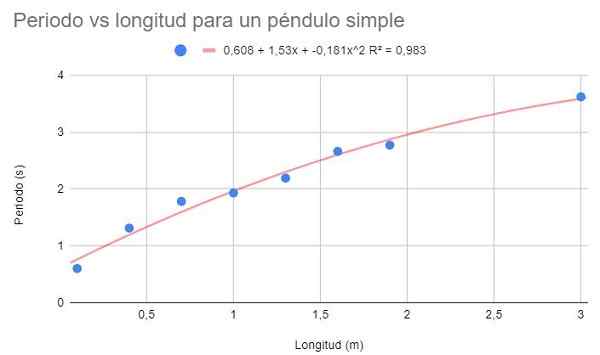Figura 4. Exercício gráfico 3 gráfico. Fonte: f. Zapata.

Com o ajuste polinomial do segundo grau, pode ser visto uma linha de tendência que se encaixa bem na curvatura dos dados. Da mesma forma, o coeficiente de determinação está acima do ajuste linear e abaixo do ajuste potencial.

Comparação de ajuste

Dos três ajustes mostrados, aquele com um coeficiente de determinação mais alto é o ajuste potencial (Exemplo 2).

O ajuste potencial coincide com a teoria física do pêndulo, que, como é conhecida, estabelece que o período de um pêndulo é proporcional à raiz quadrada de seu comprimento, sendo a constante da proporcionalidade 2π /√g onde g é a aceleração de gravidade.

Esse tipo de ajuste em potencial não apenas tem o maior coeficiente de determinação, mas o expoente e a proporcionalidade constante coincidem com o modelo físico. 

Conclusões

-O ajuste de regressão determina os parâmetros da função que visa explicar os dados através do método mínimo quadrado. Este método consiste em minimizar a soma da diferença quadrática entre o valor e o ajuste e o valor Yi dos dados para os valores xi dos dados. Dessa maneira, os parâmetros da função de ajuste são determinados.

-Como vimos, a função de ajuste mais comum é a linha, mas não é a única, pois os ajustes também podem ser polinômicos, potenciais, exponenciais, logaritmos e outros. 

-De qualquer forma, o coeficiente de determinação depende dos dados e do tipo de ajuste e é um indicativo da bondade do ajuste aplicado.

-Finalmente, o coeficiente de determinação indica a porcentagem da variabilidade total entre o valor e os dados em relação ao valor ŷ do ajuste para o X dado.

Referências

1. González c. Estatísticas gerais. Recuperado de: tarwi.La molina.Edu.educaçao Fisica
2. IACS. Instituto Aragonês de Ciências da Saúde. Recuperado de: ICS-Aragon.com
3. Salazar c. e Castillo s. Princípios de estatísticas básicas. (2018). Recuperado de: dspace.Uce.Edu.EC
4. Superprof. Coeficiente de determinação. Recuperado de: superprof.é
5. USAC. Manual de Estatística Descritiva. (2011). Recuperado de: estatísticas.Engenharia.USAC.Edu.Gt.
6. Wikipedia. Coeficiente de determinação. Recuperado de: é.Wikipedia.com.