Teste de Tukey no que é, mestre, exercício resolvido

O Teste de Tukey É um método que visa comparar médias individuais de uma análise de variação de várias amostras em.

O teste, apresentado em 1949 por John.C. Tukey, permite discernir se os resultados obtidos são significativamente diferentes ou não. Também é conhecido como o Teste de diferença honestamente significativa (Teste HSD de Tukey por suas siglas em inglês).

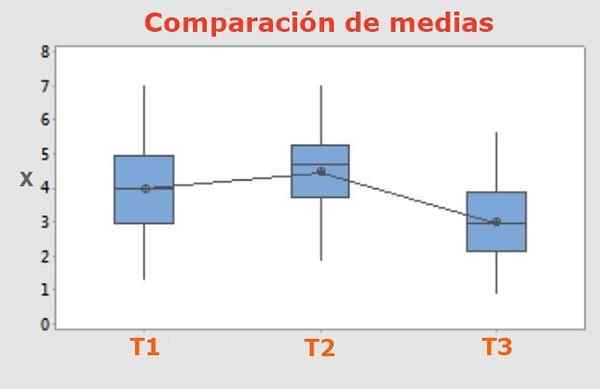
figura 1. O teste de Tukey permite discernir se as diferenças de resultado entre três ou mais tratamentos diferentes aplicados a três ou mais grupos de características iguais, têm valores médios significativos e honestamente diferentes.

Em experimentos em que se compara entre três ou mais tratamentos diferentes aplicados ao mesmo número de amostras, é necessário discernir se os resultados são significativamente diferentes ou não.

Dizem que um experimento é equilibrado quando o tamanho de todas as amostras estatísticas é o mesmo em cada tratamento. Quando o tamanho da amostragem é diferente para cada tratamento, existe um experimento não balanceado.

Às vezes, não é suficiente com uma análise de variação (ANOVA) saber se na comparação de diferentes tratamentos (ou experimentos) aplicados a várias amostras que eles cumprem a hipótese nula (HO: "Todos os tratamentos são os mesmos") ou pelo contrário Atende à hipótese alternativa (ha: "pelo menos um dos tratamentos é diferente").

O teste de Tukey não é único, há muito mais evidências para comparar meios de amostra, mas este é um dos mais conhecidos e aplicados.

[TOC]

Comparador e mesa de Tukey

Na aplicação deste teste, um valor é calculado C Chamou o Comparador de Tukey cuja definição é a seguinte:

W = Q √ (MSE /R)

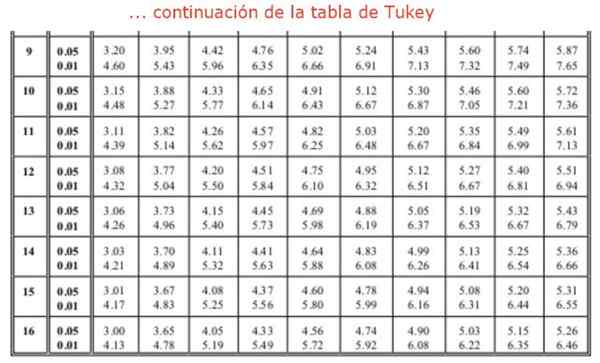
Onde o fator q É obtido de uma tabela (tabela de tukey), que consiste em fileiras de valores q Para um número diferente de tratamentos ou experimentos. As colunas indicam o valor do fator q Para diferentes graus de liberdade. Normalmente as tabelas disponíveis têm meios relativos de 0.05 e 0.01.

Pode atendê -lo: pendente de uma linha: fórmula e equações, representação, exemplos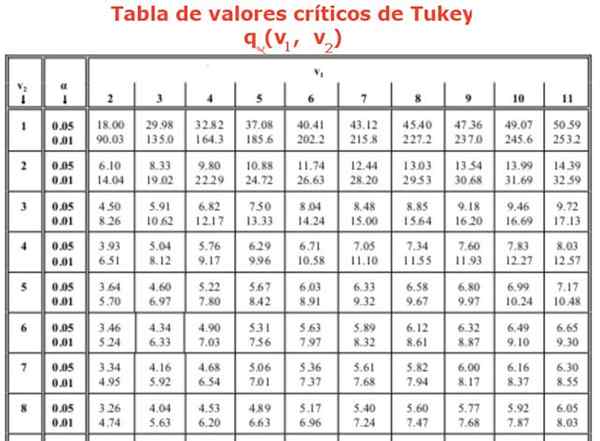

Nesta fórmula, dentro da raiz quadrada, o fator MSE aparece (quadrado médio do erro) dividido por r, o que indica o número de repetições. O MSE é um número que normalmente é obtido de uma análise de variações (ANOVA).

Quando a diferença entre dois valores médios excede o valor C (Comparador de Tukey), conclui -se que essas são médias diferentes, mas se a diferença for menor que o número de Tukey, são duas amostras com valor médio estatisticamente idêntico.

O número W também é conhecido como número HSD (diferença honestamente significativa).

Esse número apenas de comparador pode ser aplicado se o número de amostras aplicadas para o teste de cada tratamento for o mesmo em cada um deles.

Experimentos desequilibrados

Quando, por algum motivo, o tamanho das amostras é diferente em cada tratamento para comparar, o procedimento descrito acima difere um pouco e é conhecido como Teste de Tukey-Kramer.

Agora um número é obtido C Comparador para cada par de tratamentos eu j:

w (i, j) = q √ (½ mse /(ri +rj))

Nesta fórmula, o fator que é obtido da mesa de Tukey. Referido fator que depende do número de tratamentos e dos graus de liberdade de erro. r_Yo É o número de repetições no tratamento i, enquanto r_J É o número de repetições no tratamento J.

Exemplo de caso

Um criador de coelho quer fazer um estudo estatístico confiável que indica saber qual das quatro marcas de alimentos engordando de coelho é a mais eficaz. Para o estudo, ele forma quatro grupos com seis meses e meio de coelhos que até aquele momento tinham as mesmas condições alimentares.

Do experimento ao primeiro grupo, é chamado A1 porque se alimenta dos alimentos da marca 1, da mesma forma que o grupo A2, A3 e A4. Uma tabela é feita onde o ganho de peso (em libras) de cada amostra após um mês de alimentos com as diferentes marcas de alimentos é registrado, obtendo os seguintes resultados: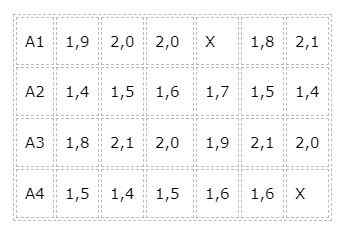Embora tenha começado com um experimento equilibrado, no sentido de que o número de coelhos aos quais o tratamento seria aplicado era o mesmo, o experimento não pôde ser finalizado dessa maneira.

Pode atendê -lo: homotecia negativa

As razões foram que, nos grupos A1 e A4, ocorreram mortes devido a causas não atribuíveis aos alimentos, uma vez que um dos coelhos foi picado por um inseto e, no outro caso, a morte foi certamente a causa de um defeito congênito. Para que os grupos sejam desequilibrados e depois é necessário aplicar o teste de Tukey-Kramer.

Exercício resolvido

Para não estender muito os cálculos, um caso de experimento equilibrado será tomado como um exercício resolvido. Os seguintes serão tomados como dados:

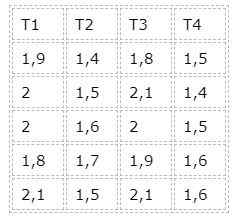
Nesse caso, existem quatro grupos correspondentes a quatro tratamentos diferentes. No entanto, observamos que todos os grupos têm o mesmo número de dados, então é um caso equilibrado.

Para realizar a análise ANOVA, a ferramenta que é incorporada à planilha de LibreOffice. Outras planilhas como Excel Eles têm essa ferramenta para análise de dados incorporada. Abaixo está uma tabela de resumo que resultou após a análise de variância (ANOVA):

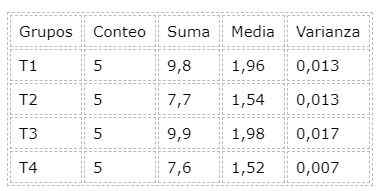
Da análise de variação, há também o valor p, que, por exemplo, é 2,24e-6 bem abaixo de 0.05 do nível de significância, que leva diretamente à rejeição da hipótese nula: todos os tratamentos são iguais. 

Ou seja, entre os tratamentos, alguns têm valores médios diferentes, mas você precisa saber quais são os significativos e honestamente diferentes (HSD) do ponto de vista estatístico usando o teste de Tukey.

Para encontrar o número w ou como o número HSD também é conhecido, exigimos o quadrado médio do erro MSE. A partir da análise ANOVA, obtém -se que a soma dos quadrados dentro dos grupos é SS = 0,2; E o número de graus de liberdade dentro dos grupos é df = 16 com esses dados que podemos encontrar MSE:

Pode atendê -lo: Papomudas

MSE = ss/df = 0,2/16 = 0,0125

Também é necessário encontrar o fator q de Tukey, usando a tabela. É procurada na coluna 4 que corresponda aos 4 grupos ou tratamentos para comparar e a linha 16, uma vez que a análise da ANOVA mostrou 16 graus de liberdade dentro dos grupos. Isso nos leva a um valor de q igual a: Q = 4,33 correspondente a 0,05 significância ou 95% de confiabilidade. Finalmente, é encontrado o valor para a "diferença honestamente significativa":

W = hsd = Q √ (MSE /R) = 4,33 √ (0,0125 /5) = 0,2165

Para saber quais são os grupos ou tratamentos honestamente diferentes, você precisa conhecer as médias de cada tratamento:

Também é necessário conhecer as diferenças entre os valores médios de pares de tratamentos, o que é mostrado na tabela a seguir:

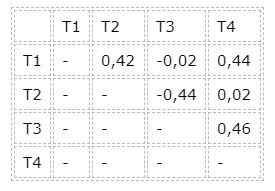Grupos T3 e T1, assim como os grupos T2 e T4, são de resultados idênticos. Portanto, os grupos honestamente diferentes são grupos T1 e T2 ou T3 e T4, uma vez que a diferença em seus valores médios excede o valor HSM do teste de Tukey.

Conclui -se que os melhores tratamentos, em termos de maximizar o resultado são o T1 ou o T3, que são indiferentes do ponto de vista estatístico. Para escolher entre T1 e T3, outros fatores fora da análise apresentados aqui devem ser procurados. Por exemplo, preço, disponibilidade, etc.

Referências

1. Cochran William e Cox Gertrude. 1974. Projetos experimentais. Trillas. México. Terceira reimpressão. 661p.
2. Snedecor, g.C. E Cochran, W.G. 1980. Métodos estatísticos. Sétima ed. Iowa, a imprensa da Universidade Estadual de Iowa. 507p.
3. Aço, r.G.D. E Torrie, J.H. 1980. Princípios e procedimentos de estatística: uma abordagem biométrica (2ª ed.). McGraw-Hill, Nova York. 629p.
4. Tukey, J. C. 1949. Meios de comparação individuais na análise de variância. Biometrics, 5: 99-114.
5. Wikipedia. Teste de Tukey. Recuperado de: em.Wikipedia.com