Fórmula da lei de Biot-Savart, Demonstração, Aplicações, Exercícios

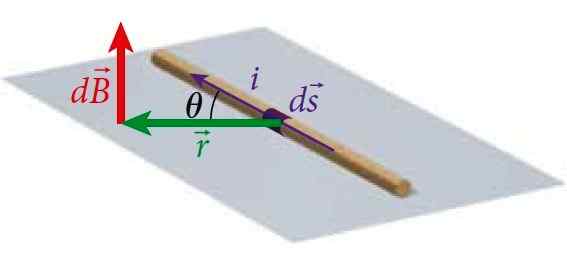
O Lei Biot-Savart estabelece uma relação entre o campo magnético DB  em um ponto P, produzido por um fio fino que transporta um I e cujo comprimento diferencial é Ds. Esta lei é usada para encontrar o campo magnético das distribuições atuais através do Princípio da superposição. 

Isso significa que, para calcular o campo magnético total no ponto P, devemos adicionar todas as contribuições que cada parte diferencial Ds do fio contribui. E esta soma é feita através de uma integral realizada em toda a distribuição atual.

figura 1. Um segmento de arame transporta uma corrente I, que produz um campo magnético em um ponto P a uma certa distância do fio, que é calculado pela lei Biot-Savart. Fonte: Bauer, W. Física para engenharia e ciências.

Dessa maneira, você pode calcular o campo que produz fios com corrente de diferentes geometrias.

A lei de Biot-Savart recebeu o nome dos dois físicos franceses que a descobriram em 1820: Jean Marie Biot (1774-1862) e Felix Savart (1791-1841). Para conseguir isso, eles tiveram que estudar a intensidade e a forma do campo magnético produzido por inúmeras distribuições atuais.

[TOC]

Fórmula

A expressão matemática da lei de Biot-Savart é a seguinte:

Ele mantém analogias com o equivalente a calcular o campo elétrico: a lei de Coulomb, apenas que o campo magnético DB em p é perpendicular para o avião onde o fio está localizado. Podemos ver isso na Figura 1.

A expressão anterior também pode ser escrita da seguinte forma:

Em ambas as expressões, r É o vetor de posição, direcionado a partir do elemento atual de identificaçãos até o ponto em que você deseja calcular o campo.

Pode atendê -lo: Conservação do Momento Linear: Princípio, Exemplos, Exercícios.

Por sua parte, r Com um sotaque circunflejo, é o vetor unitário que é direcionado em sua mesma direção e direção, mas com um módulo igual a 1. O vetor r Está representado da seguinte maneira:

Por esse motivo, substituindo a equação anterior -a que tem r³ No denominador- a expressão r é imediatamente alcançada² No denominador.

Além dos vetores acima mencionados, a fórmula contém a constante μ_qualquer, chamar Permeabilidade a vácuo e cujo valor é:

μ_qualquer = 4π x10^-7 T.m/ a.

Se queremos calcular o vetor de campo magnético, é necessário integrar toda a distribuição atual, para a qual precisamos dos dados sobre sua geometria:

O produto vetorial e a regra da mão direita

A lei de Biot-Savart envolve um produto vetorial entre vetores de identificaçãos e r. O resultado de um produto vetorial entre dois vetores também é um vetor.

Nesse caso, o módulo de produto do vetor de identificaçãos x r é: (IDS) ⋅r⋅senθ, onde θ é o ângulo entre IDs e r, Como mostrado na Figura 1.

Dessa maneira, a magnitude do campo DB É dado por:

A direção e o significado podem ser determinados com a regra da mão direita, que é ilustrada nesta figura:

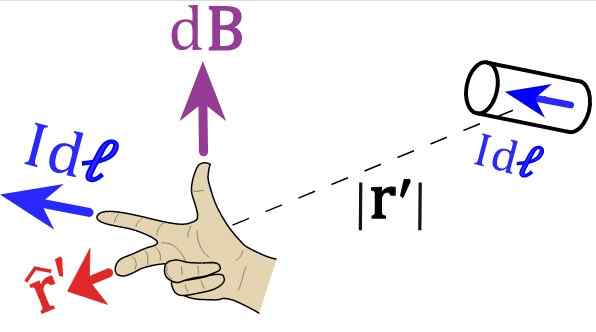Figura 2. Regra da mão direita para a lei de Biot-Savart. Fonte: Wikimedia Commons.

Convidamos o leitor a posicionar sua mão direita seguindo os vetores das Figuras 1 e 2. Para a Figura 1, o dedo indicador deve apontar para a esquerda, seguindo o IDs ou ideu, O dedo médio aponta de acordo com o vetor r unitário.

E finalmente o polegar é direcionado e esta é a direção do campo magnético.

Pode atendê -lo: elipsóide: características e exemplos

Demonstração da Lei Biot-Savart

A lei de Biot-Savart é eminentemente experimental, o que significa que sua formulação vem de muitas observações sobre o comportamento do campo magnético produzido pelos fios atuais.

Observações Biot e Savart

Essas foram as observações dos cientistas franceses sobre o campo magnético DB:

-A magnitude de DB é inversamente proporcional a r².

-Também é diretamente proporcional à magnitude do elemento atual, que é chamado de IDs E também para sen θ, onde θ é o ângulo entre os vetores Ds e r.

-dB é perpendicular a ambos os IDs -a direção da corrente e r.

-Diversos de dB é tangencial a um círculo de rádio r Centro de fio. Em outras palavras, o campo B produzido por um segmento atual consiste em circunferências concêntricas para o estéril.

-O significado em que gira B É dado pela regra do polegar direito: o polegar direito é apontado na direção da corrente e os quatro dedos restantes são enrolados ao redor do fio, seguindo a circulação do campo.

Todas essas observações são combinadas na expressão matemática da lei descrita anteriormente.

Aplicações de lei de Biot-Savart

Quando a distribuição atual tem alta simetria, a integral pode ser facilmente resolvida, vamos ver alguns casos:

Arame retilíneo e fino

Um fio retilíneo de comprimento l transporta uma corrente i, como aquele que aparece na figura.

Ilustra a geometria necessária para o cálculo do campo. Isso é perpendicular à folha de papel, extrovertida para o avião se a corrente fluir da esquerda para a direita e recebendo o contrário (verifique -o com a regra da mão direita).

Pode atendê -lo: paramagnetismo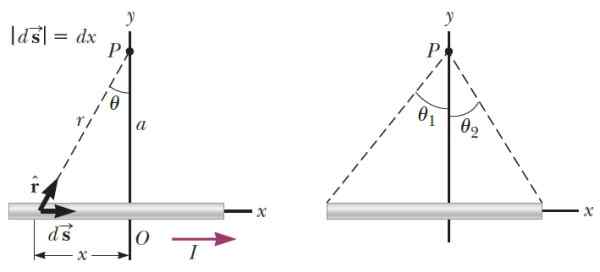Figura 3.- À esquerda, a geometria necessária para calcular o campo magnético que produz um segmento de fio fino no ponto P. À direita os ângulos que determinam a posição de P em relação às extremidades do segmento. Fonte: Serway, r. Física para Ciência e Engenharia.

Ser k  O vetor de unidade na direção perpendicular ao plano, depois de realizar o processo de integração, o campo magnético que o fio produz em P é:

Espira circular

O loop circular de rádio para Ele transporta uma corrente como mostrado na figura e produz um campo magnético DB -em verde escuro- no ponto P no eixo axial, à distância x do Centro.

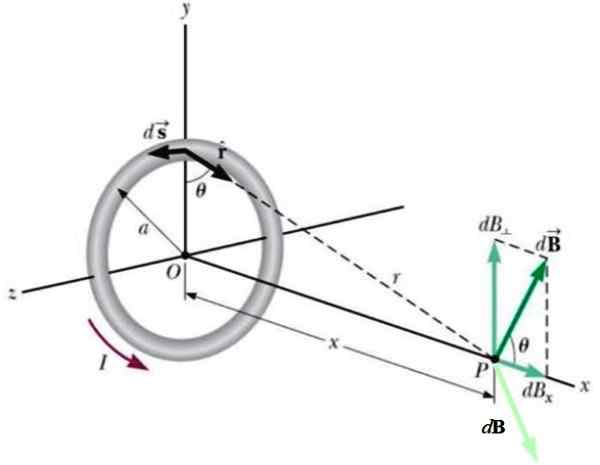Figura 4.- Geometria para o cálculo do campo produzido pela SPASE circular no ponto P no eixo axial. Fonte: Wikimedia Commons.

Outro elemento atual localizado no lado oposto produziria outra contribuição para o DB (verde claro), de modo que seu componente vertical seja cancelado com o primeiro.

O resultado é que o campo magnético líquido é horizontal, por isso é integrado apenas a esses componentes, resultando em:

Exercício resolvido

Há um fio extremamente longo que transporta uma corrente de 2 para fluir como mostrado na imagem. Calcule a magnitude do campo magnético a uma distância radial de 5 cm do fio.

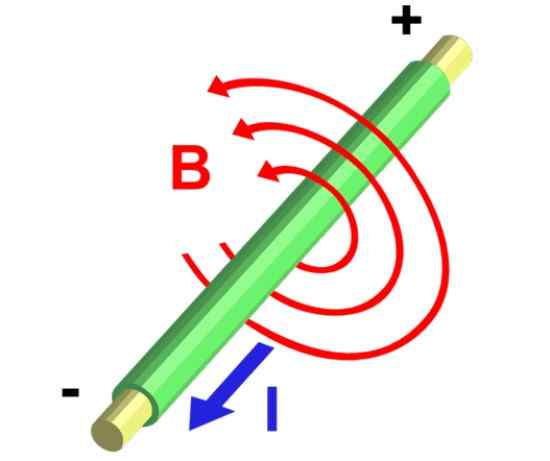Figura 5.- Linhas de campo magnéticas de um segmento de fio retilíneo que transporta corrente. Fonte: Wikimedia Commons.

Solução

Como é um fio muito longo, podemos pegar a expressão para o segmento retilíneo e fazer θ₁= 0º e θ₂ = 180º para ângulos de limite. Isso é suficiente para o comprimento do fio para armazenar o infinito.

Dessa maneira, teremos o campo é:

Isso simplifica:

Agora substituímos os valores da instrução:

I = 2 a

R = 5 x10^-2 m

μ_qualquer= 4π x10^-7 T.m/ a

A direção e o sentido de B Eles são mostrados na Figura 5, onde a direção que sai da folha foi tomada como k.

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB).
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Resnick, r. 1999. Físico. Vol. 1. 3ª ed. em espanhol. Empresa Editorial Continental S.PARA. claro.V.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.
6. Serway, r., Jewett, J. 2008. Física para Ciência e Engenharia. Volume 2. 7º. Ed. Cengage Learning.