Interpolação de Lagrange

Qual é a interpolação de Lagrange?

A interpolação de Lagrange é um método numérico de aproximação de funções, que utiliza um polinômio que passa por certos pontos conhecidos da função que se destina a se aproximar.

Se a função aproximada for suave, mesmo fora dos valores dados ou conhecidos, o polinomial leva valores próximos aos da função do interesse, especialmente se esses valores estiverem entre os pontos dados. É por isso que o polinômio é considerado uma boa abordagem para a função.

figura 1.- Fórmula para construir polinômios de Lagrange. Fonte: f. Zapata.

Agora, suponha que você queira aproximar uma função f (x) dos quais apenas seus valores são conhecidos em alguns x-_Yo-, com Yo de 0 até N-1. Isto é, eles se conhecem n pontos (x-_Yo, e_Yo) com e_Yo = f (x_Yo), Onde o índice Yo Vai de 0 até N-1.

No método de interpolação de LaGrange, o polinomial que se aproxima da função f (x) É um polinômio P (x) de grau N-1, construído pela combinação linear de n Polinômios eu_Yo(x) de grau N-1. Estes são os Lagrange Polynomials, que são expressos da seguinte forma:

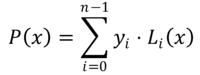
Os valores de e_Yo Eles representam as ordenadas correspondentes à abcissa x_Yo Onde a função f (x) Sabe -se, ou seja: e_Yo = f (x_Yo).

Lagrange Polynomials

Através de combinações lineares entre eles, os polinômios de Lagrange atuam como base para a construção de polinômios de grau N -1 que servirá para interpolar o n pontos conhecidos.

A notação para os polinômios é L_Yo(x), com o índice I na faixa de 0 a N-1. A fórmula para estabelecer polinômios de Lagrange é a seguinte:

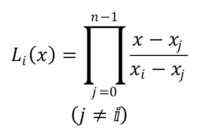
O símbolo mostrado indica que o produto de monômios n -1 deve ser realizado, a partir do polinomial j = 0.

Características dos polinômios de Lagrange

1.- Os polinômios de Lagrange são exatamente os mesmos que a unidade quando avaliados na abcissa correspondentes ao seu índice, ou seja::

eu_Yo(x_Yo) = 1

2.- Eles são cancelados na abscissa dos pontos de interpolação com o índice diferente do do mesmo polinômio:

Pode servir a você: Estatística descritiva: história, características, exemplos, conceitos

eu_Yo(x_J) = 0, com i ≠ j.

3.- Tomando outros valores de abcissa diferente dos pontos de interpolação, os polinômios de Lagrange adquirem valores entre -1 e +1.

4.- Para obter polinômios de Lagrange, é necessário conhecer a abcissa dos pontos para interpoch.

Polinômios de Segundo Decorda

Polinômios de Segundo Decorda Lagrange são aqueles que são usados ​​com mais frequência quando você deseja fazer uma interpolação de três pontos.

Suponha que a função interpolar seja conhecida em três pontos, que são:

(x₀,e₀); (x₁, e₁); (x₂, e₂)

Então seus polinômios lagrange correspondentes eu₀, eu₁ e eu₂ Eles ficam assim:

eu₀(x) = [(x - x₁) / (X₀ - x₁)] [(x - x₂) / (X₀ - x₂)]

eu₁(x) = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)]

eu₂(x) = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)]

Deve -se notar que eu₀(x₀) = L₁(x₁) = L₂(x₂) = 1, enquanto que eu_Yo(x_J) = 0 sempre que Yo≠ j.

Polinômio de interpolação do segundo grau

É importante observar que no polinomial de interpolação de LaGrange, as ordenadas dos pontos de interpolação são fatores polinomiais de Lagrange.

Dessa maneira, uma vez que os polinômios são obtidos para certos valores da abcissa, eles servem para calcular o polinômio de interpolação de várias funções, desde que o ordenado na abscissa previamente fixo seja conhecido.

No caso de uma interpolação da segunda série:

P (x) = f (x₀) EU₀(x) + f (x₁) EU₁(x) + f (x₂) EU₂(x)

E p (x) se aproxima da função f (x) no intervalo (x₀, x₂).

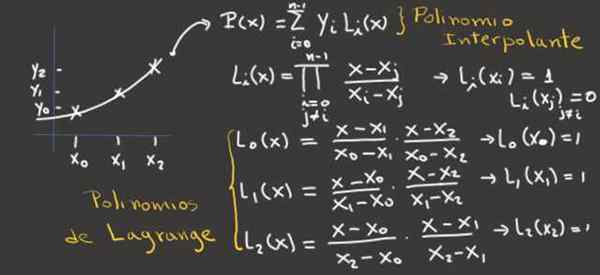Figura 2.- Esta imagem mostra como obter os polinômios de Lagrange para três pontos de interpolação e deles, o polinômio interpoling. Fonte: f. Zapata.

Exemplos

Exemplo 1

Encontre os polinômios de Lagrange correspondentes a três pontos de abcissa x₀= 0, x₁= 1 e x₂= 2.

Como visto na seção anterior, esses polinômios serão:

Pode atendê -lo: função superjectiva: definição, propriedades, exemplos

eu₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( x² - 3x + 2)

eu₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

eu₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - x)

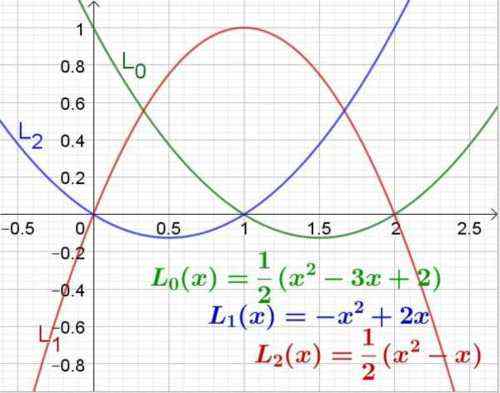Figura 3. Polinômios de Lagrange para os valores de Abcissa 0, 1 e 2. Fonte: f. Zapata.

Exemplo 2

Você quer aproximar a função f (x) = arcan (x) No intervalo [0, 2]. Desta função, apenas seus valores são conhecidos por x₀= 0, x₁= 1 e x₂= 2, quais são respectivamente e₀= 0, e₁= π/4 = 0,785 e e₂= 1.107.

Portanto, você precisa encontrar o polinômio interpolador P (x) Aproximando f (x) No intervalo indicado.

No Exemplo 1, os polinômios de Lagrange já foram determinados para os valores de abcissa indicados nesta declaração, portanto, não é necessário repetir o cálculo. O Polinomial interpoling será agora:

P (x) = f (x₀) EU₀(x) + f (x₁) EU₁(x) + f (x₂) EU₂(x)

Que é equivalente a:

P (x) = y₀ eu₀(x) + e₁ eu₁(x) + e₂ eu₂(x)

Neste caso específico, é:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0,785 ∙ (- x² + 2x) + 1.107 ∙ (½) (x² - x)

O acima é simplificado para:

P (x) = 0,785 ∙ (- x² + 2x) + 1.107 ∙ (½) (x² - x)

E finalmente permanece:

P (x) = -0,2315 ∙ x x² + 1.0165 ∙ x

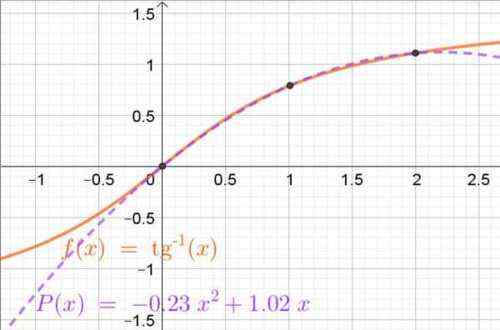Figura 4. O polinômio interpoling obtido através de polinômios de Lagrange que se aproxima da função tangente do arco no intervalo (0, 2). Os pontos de interpolação também são mostrados. Fonte: f. Zapata.

Exercícios

Exercício 1

Obtenha polinômios adequados para ter uma abordagem da função:

f (x) = sin (x)

No intervalo [0, π] e com cinco pontos de interpolação.

Solução

Em primeiro lugar, são determinadas a abscissa dos pontos de interpolação, que são escolhidos iguais e incluindo as extremidades do intervalo de aproximação. Com isso você tem:

x₀= 0; x₁= π/4; x₂= π/2; x₃= 3 π/4; x₄= π.

Pode atendê -lo: desigualdade do triângulo: demonstração, exemplos, exercícios resolvidos

Como f (x) é cancelado nos pontos extremos, não será necessário obter os polinômios lagrange l₀ e eu₄.

Polinômios l₁, eu₂ e eu₃ são:

eu₁ = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)] [(x - x₃) / (X₁ - x₃)] [(x - x₄) / (X₁ - x₄)]

eu₂ = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)] [(x - x₃) / (X₂ - x₃)] [(x - x₄) / (X₂ - x₄)]

eu₃ = [(x - x₀) / (X₃ - x₀)] [(x - x₁) / (X₃ - x₁)] [(x - x₂) / (X₃ - x₂)] [(x - x₄) / (X₃ - x₄)]

Agora substituímos o valor da abscissa:

eu₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

eu₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

eu₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Os denominadores são resolvidos:

eu₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - - 3π/4)]

eu₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

eu₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

É simplificado e reagrupado para obter:

eu₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

eu₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

eu₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Exercício 2

Obtenha o polinômio de interpolação que se aproxima da função Sen (x) no intervalo [0, π] com os cinco pontos de interpolação escolhidos no Exercício 1 e seus respectivos polinômios de Lagrange.

Solução

O polinômio de interpolação é:

P (x) = sin (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * L₃ + Sen (π) * L4

Avaliar o seio e multiplicar a função é:

P (x) = (√2/2) l₁ + 1 * l₂ + (-√2/2) l₃

Após um trabalho algébrico árduo, o polinomial de interpolação é:

P (x) = 2. 7481 x⁴ -quinze. 138 x³ +23. 467 x² - 9. 5236 x

Referências

1. Goodman, a. eu. H. mil novecentos e noventa e seis. Álgebra e trigonometria com geometria analítica. Pearson Education.
2. Harpe, p. d. (2000). Tópicos na teoria do grupo geométrico. University of Chicago Press.
3. Hazewinkel, m. (2001). Interpolação linear ", Enciclopédia da Matemática.
4. Hoffmann, e. (2002). À cronologia da interpolação: da astronomia antiga ao processamento moderno de sinal e imagem. Anais do IEEE.
5. Wikipedia. Interpolação polinomial de Lagrange. Recuperado de: Wikipedia.com