Função excessiva, propriedades, exemplos

A função excessiva É qualquer relacionamento em que cada elemento pertencente ao Codominium é uma imagem de pelo menos um elemento de domínio. Também conhecido como função sobre, Eles fazem parte da classificação das funções sobre a maneira como seus elementos estão relacionados.

Por exemplo, uma função F: a → B definido por F (x) = 2x

Que é lido "F isso vai de PARA até B definido por F (x) = 2x "

Touch Defina os conjuntos de partida e chegada A e b.

A: 1, 2, 3, 4, 5 Agora os valores ou imagens que cada um desses elementos serão liberados quando avaliados em F, Eles serão os elementos do codomínio.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Assim formando o conjunto B: 2, 4, 6, 8, 10

Pode -se concluir que:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 definido por F (x) = 2x é uma função excessiva

Cada elemento do codomínio deve ser pelo menos uma operação da variável independente através da função em questão. Não há limitação de imagem, um elemento de codomínio pode ser uma imagem de mais de um elemento do domínio e continuar lidando com um função excessiva.

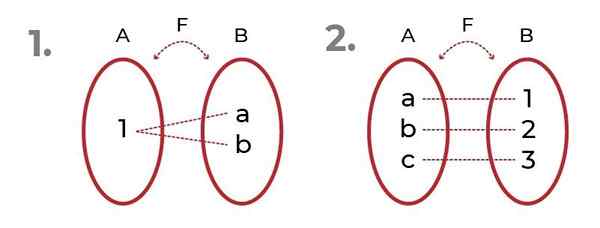
A imagem mostra 2 exemplos com funções onjetivas.

Fonte: Autor

No primeiro, observa -se que as imagens podem ser referidas ao mesmo elemento, sem comprometer o Superjectividade da função.

No segundo, vemos uma distribuição equitativa entre domínio e imagens. Isso dá origem a Função bijectiva, onde os critérios de Função injetiva e função superjectiva.

Outro método para identificar funções onjetivas, é verificar se o codomínio é igual à classificação da função. Isso significa que se o conjunto de chegada for igual às imagens fornecidas pela função ao avaliar a variável independente, A função é demais.

[TOC]

Propriedades

Considerar Superjetivo O seguinte deve ser cumprido a uma função:

Ser F: d_F → C_F

∀ B ℮ C_F  E para ℮  D_F   / F (a) = b

Esta é a maneira algébrica de estabelecer isso Para todos "B" que pertence a C_F Há um "A" que pertence a D_F  de modo que a função f avaliada em "A" é igual a "B". 

Pode atendê -lo: propriedades radicais

A superjecutividade é uma peculiaridade das funções, onde o codomínio e a classificação são semelhantes. Assim, os elementos avaliados na função compõem o conjunto de chegada.

Condicionamento de funções

Às vezes uma função que não é Superjetivo, pode sofrer um determinado condicionamento. Essas novas condições podem transformá -lo em um função excessiva.

Todos os tipos de modificações no domínio e codomínio da função são válidos, onde o objetivo é atender às propriedades de superjecução no relacionamento correspondente.

Exemplos: exercícios resolvidos

Para atender às condições de Superjectividade Diferentes técnicas de condicionamento devem ser aplicadas, a fim de garantir que cada elemento do codomínio esteja dentro do conjunto de imagens da função.

Exercício 1

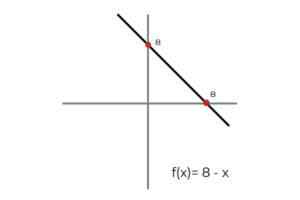
• Seja a função F: r → R definido pela linha F (x) = 8 - x

A: [todos os números reais]

Fonte: Autor

Nesse caso, a função descreve uma linha contínua, que abrange todos os números reais, tanto em seu domínio quanto. Porque a classificação da função R_F É igual ao codomínio R Pode -se concluir que:

F: r → R definido pela linha F (x) = 8 - x é uma função excessiva.

Isso se aplica a todas as funções lineares (funções cujo maior grau da variável é uma).

Exercício 2

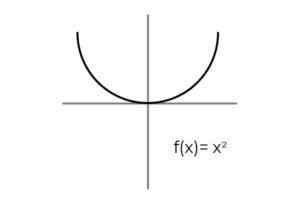
• Estude a função F: r → R definido por F (x) = x² : Defina se for um função excessiva. Caso não esteja, mostre o condicionamento necessário para torná -lo sobrejetivo.

Fonte: Autor

A primeira coisa a considerar é o codomínio de F, que consiste em números reais R. Não há como a função lançar valor negativo, que exclui os reais negativos entre as imagens possíveis.

Condicionando o codomínio intervalo [0 , ∞ ]. É evitado deixar elementos do co -alomio sem se relacionar F.

As imagens são repetidas para pares de elementos da variável independente, como x = 1 e x = - 1.  Mas isso afeta apenas o Injetividade  da função, não sendo um problema para este estudo.

Pode atendê -lo: derivados sucessivos

Dessa maneira, pode -se concluir que:

F: r  →[0, ∞ ) definido por F (x) = x²    É uma função superjectiva

Exercício 3

• Defina as condições do codomínio que eles fariam superjetivo para funções

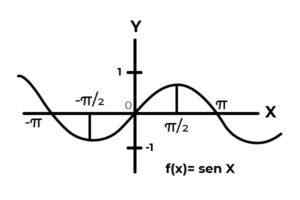
F: r  → R definido por F (x) = sin (x)

F: r  → R definido por F (x) = cos (x)

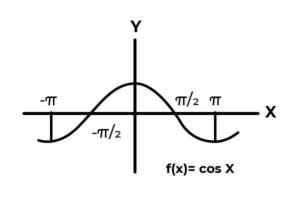Fonte: Autor Fonte: Autor.

O comportamento das funções trigonométricas é semelhante ao das ondas, sendo muito comum para encontrar repetições da variável dependente entre as imagens. Também na maioria dos casos, o alcance da função é limitado a um ou mais setores da linha real.

Este é o caso das funções seno e cosseno. Onde seus valores flutuam no intervalo [-1, 1]. O referido intervalo deve condicionar o codomínio para alcançar o envelope da função.

F: r  →[ -onze ] definido por F (x) = sin (x)  É uma função superjectiva

F: r  →[ -onze ]definido por F (x) = cos (x) É uma função superjectiva

Exercício 4

• Estude a função

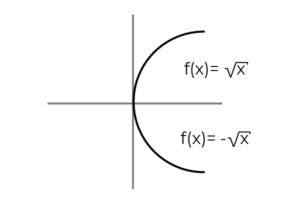
F: [0, ∞ ) → R definido por F (x) = ± √x   denotar se for um função excessiva

Fonte: Autor

A função F (x) = ± √x  Tem a particularidade que define 2 variáveis ​​dependentes em cada valor de "x" . Isto é, o intervalo recebe 2 elementos para cada um que é realizado no domínio. Um valor positivo e negativo para cada valor de "x" deve ser verificado para cada valor de "x".

Ao observar a montagem inicial, observa -se que o domínio já foi restrito, isso para evitar as indeterminações produzidas ao avaliar um número negativo dentro de uma raiz de torque.

Ao verificar o intervalo da função, mostra que cada valor de codomínio pertence ao intervalo.

Dessa maneira, pode -se concluir que:

F: [0, ∞ ) → R definido por F (x) = ± √x  É uma função superjectiva

Pode atendê -lo: vetores simultâneos: características, exemplos e exercícios

Exercício 4

• Estude a função F (x) = ln x  denotar se for um função excessiva. Condicionar os conjuntos de chegada e partida para adaptar a função aos critérios da superjectividade.

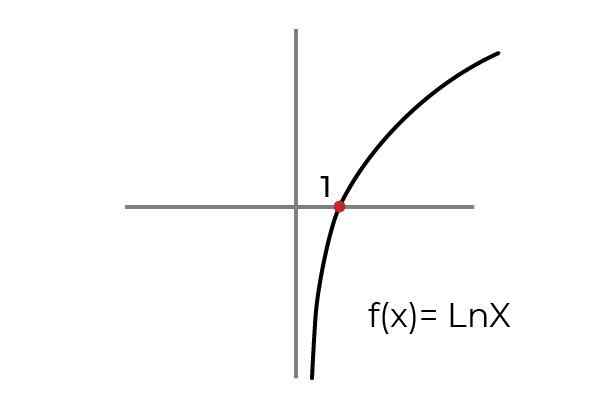Fonte: Autor

Como mostrado no gráfico da função F (x) = ln xé definido para os valores de "x" maior que zero. Enquanto os valores de "e" ou imagens podem assumir qualquer valor real.

Dessa forma, podemos restringir o domínio de F (x) = para o intervalo (0 , ∞ )

Enquanto a classificação da função pode ser mantida como conjunto de números reais R.

Considerando isso, pode -se concluir que:

F: [0, ∞ ) → R definido por F (x) = ln x  É uma função superjectiva

Exercício 5

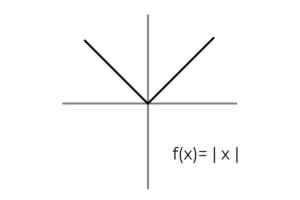
• Estudo função de valor absoluto F (x) = | x | e designar os conjuntos de chegada e partida que são coletados para os critérios para a alteração.

Fonte: Autor

O domínio da função é cumprido para todos os números reais R. Dessa maneira.

O codomínio da função é estabelecida, equalizando -a ao alcance do mesmo

[0 , ∞ )

Agora pode -se concluir que:

F: [0, ∞ ) → R definido por F (x) = | x |  É uma função superjectiva

Exercícios propostos

1. Verifique se as seguintes funções são superjetivas:

• F: (0, ∞ ) → R definido por F (x) = log (x + 1)
• F: r → R definido por F (x) = x³
• F: r →[1, ∞ )  definido por F (x) = x²  + 1
• [0, ∞ ) → R definido por F (x) = log (2x + 3)
• F: r → R definido por F (x) = seg x
• F: R - 0 → R definido por F (x) = 1 / x

Referências

1. Introdução à lógica e pensamento crítico. Merrilee h. Salmão. Universidade de Pittsburgh
2. Problemas em análise matemática. Piotr Bilar, Alfred Witkowski. Universidade de Wroclaw. Pólo.
3. Elementos da análise abstrata. MÍCHEL O'SEARCOID PhD. Departamento de Matemática. University College Dublin, Beldfield, Dublind 4
4.  Introdução à lógica e à metodologia das ciências dedutivas. Alfred Tarski, Nova York Oxford. imprensa da Universidade de Oxford.
5.  Princípios de análise matemática. Enrique Linés Escardó. Editorial reverté s. A 1991. Barcelona Espanha.