Função injetiva do que consiste, para que é e exemplos

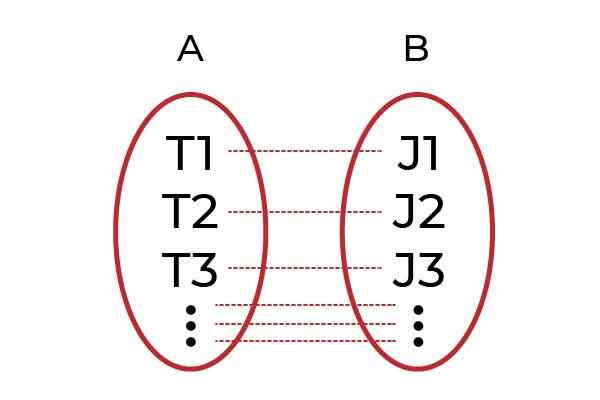
A Função injetiva É qualquer relação de elementos de domínio com um único elemento de codomínio. Também conhecido como função um a um ( onze ), fazem parte da classificação de funções sobre a maneira como seus elementos estão relacionados.

Um elemento de codomínio pode ser apenas uma imagem de um único elemento do domínio, dessa maneira os valores da variável dependente não podem ser repetidos.

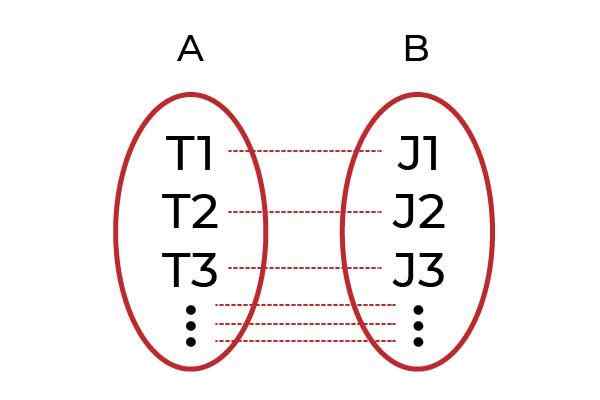Fonte: Autor.

Um exemplo claro seria agrupar homens com trabalho em um grupo A, e em um grupo B para todos os chefes. A função F Será o que associa cada trabalhador a seu chefe. Se cada trabalhador estiver associado a um chefe diferente através F, então F  Será um Função injetiva.

Considerar Injetivo O seguinte deve ser cumprido a uma função:

∀ x₁  ≠ x₂   ⇒ f (x₁ ) ≠ f (x₂ )

Esta é a maneira algébrica de dizer Para todos x₁ diferente de x₂ Você tem um f (x₁ ) Diferente de f (x₂ ).

[TOC]

O que são funções injetivas para?

A injetividade é uma propriedade de funções contínuas, pois elas garantem a alocação de imagens para cada elemento de domínio, aspecto essencial na continuidade de uma função.

Ao desenhar uma linha paralela ao eixo X No gráfico de uma função injetiva, apenas o gráfico deve ser tocado em um único ponto, independentemente de que altura ou magnitude de E A linha é desenhada. Esta é a maneira gráfica de provar a injetividade de uma função.

Outra maneira de testar se uma função é Injetivo, está limpando a variável independente X Em termos da variável dependente E. Então deve ser verificado se o domínio dessa nova expressão contiver os números reais, ao mesmo tempo que para cada valor de E há um único valor de X.

Funções ou relacionamentos de pedidos obedecem, entre outras formas, a notação F: d_F→C_F

Isso lê F isso vai de D_F para c_F

Onde a função F Relacionar os conjuntos Domínio e Codomínio. Também conhecido como conjunto de partidas e conjunto de chegada.

Pode servir a você: Amostragem aleatória: metodologia, vantagens, desvantagens, exemplos

O domínio D_F  Contém os valores permitidos para a variável independente. O codomínio C_F  É formado por todos os valores disponíveis para a variável dependente. Os elementos de C_F relacionado a D_F  Eles sabem como Intervalo de funções (r_F ).

Condicionamento de funções

Às vezes, uma função que não é injetiva, pode sofrer um determinado condicionamento. Essas novas condições podem transformá -lo em um Função injetiva. Todos os tipos de modificações no domínio e codomínio da função são válidos, onde o objetivo é atender às propriedades de injetividade no relacionamento correspondente.

Exemplos de funções injetivas com exercícios resolvidos

Exemplo 1

Seja a função F: r → R definido pela linha F (x) = 2x - 3

A: [todos os números reais]

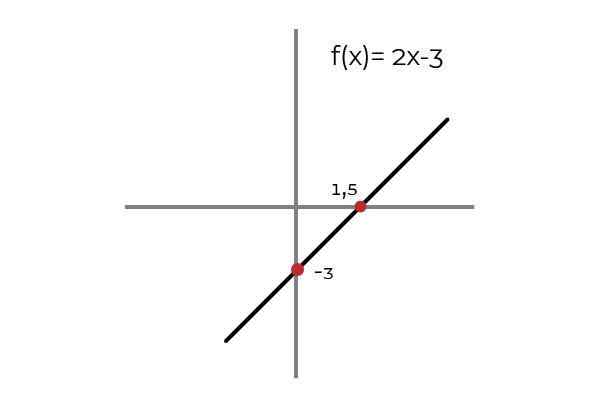Fonte: Autor.

Observa -se que, para qualquer valor de domínio, existe uma imagem no codomínio. Esta imagem é única, o que torna f uma função injetiva. Isso se aplica a todas as funções lineares (funções cujo maior grau da variável é uma).

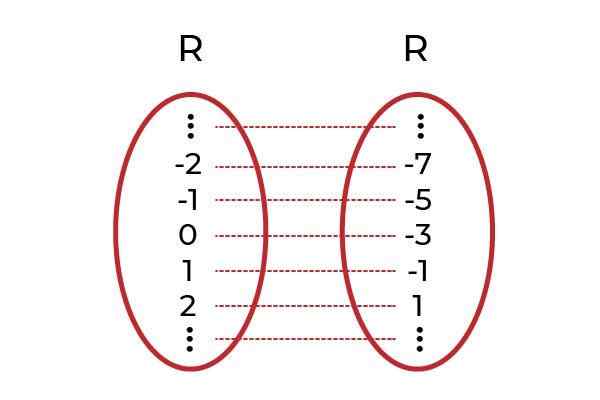Fonte: Autor.

Exemplo 2

Seja a função F: r → R definido por F (x) = x² +1

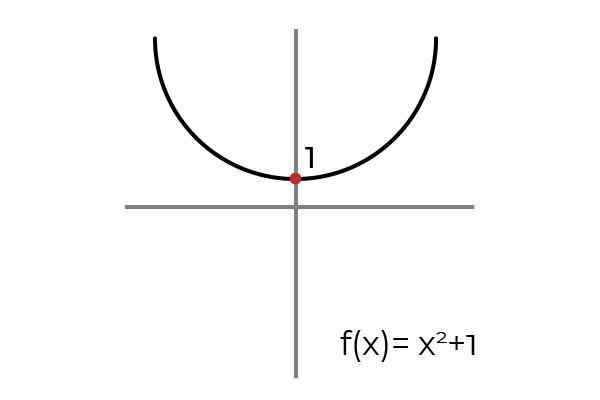Fonte: Autor

Ao desenhar uma linha horizontal, observa -se que o gráfico é encontrado em mais de uma ocasião. Por causa disso, a função F não é injetivo enquanto definido  R → R

O domínio da função está condicionado:

                                               F: r⁺ OU 0 → R

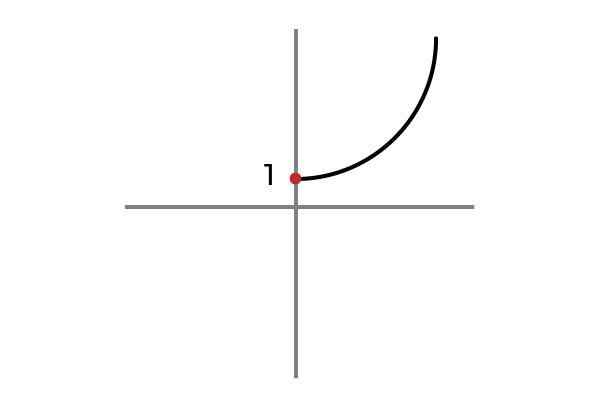Fonte: Autor

Agora a variável independente não leva valores negativos, dessa maneira é evitado para repetir resultados e a função F: r⁺ OU 0 → R definido por F (x) = x² + 1 é injetivo.

Outra solução homóloga seria limitar o domínio à esquerda, ou seja, restringir a função a tomar apenas valores negativos e zero.

O domínio da função está condicionado

                                               F: r^- OU 0 → R

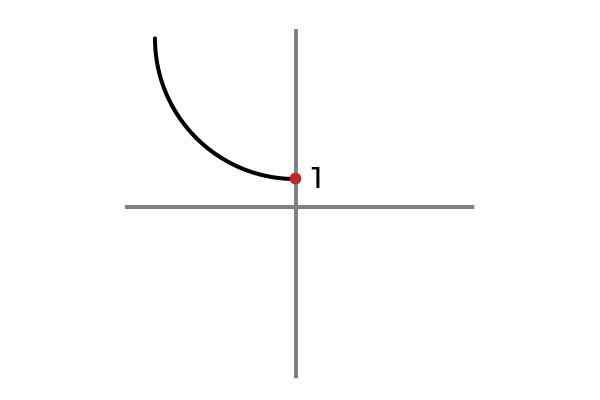Fonte: Autor

Agora a variável independente não leva valores negativos, dessa maneira é evitado para repetir resultados e a função F: r^- OU 0 → R definido por F (x) = x² + 1 é injetivo.

As funções trigonométricas têm comportamentos semelhantes às ondas, onde é muito comum encontrar repetições de valores na variável dependente. Através de condicionamento específico, com base no conhecimento prévio dessas funções, podemos limitar o domínio para atender às condições de injetividade.

Pode servir a você: coplanares pontos: equação, exemplo e exercícios resolvidos

Exemplo 3

Seja a função F: [ -π/2, π/2 ] → R definido por F (x) = cos (x)

No intervalo [[ -π/2 → π/2 ] A função cosseno varia seus resultados entre zero e um.

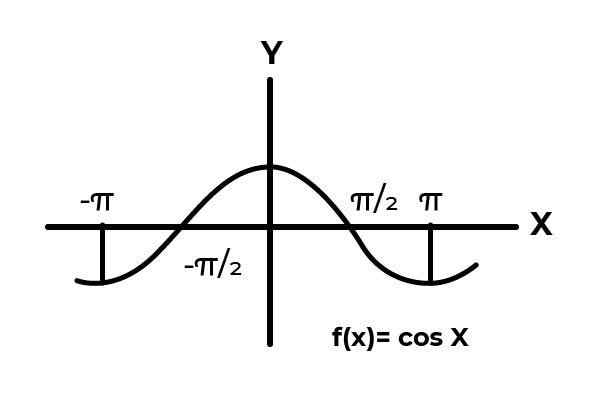Fonte: Autor.

Como pode ser visto nos gráficos. Comece do zero em x = -π/2 então atingindo um máximo de zero. É depois x = 0 que os valores começam a se repetir, até retornar a zero em x = π/2. Dessa forma, sabe -se que F (x) = cos (x) não é injetivo Para o intervalo [[ -π/2, π/2 ] .

Ao estudar os gráficos da função F (x) = cos (x) Os intervalos são observados onde o comportamento da curva se adapta aos critérios de injetividade. Como o intervalo

[0 , π ]

Onde a função varia os resultados de 1 a -1, sem repetir nenhum valor na variável dependente.

Dessa maneira, a função da função F: [0 , π ] → R definido por F (x) = cos (x). É injetivo

Existem funções não lineares em que casos semelhantes são apresentados. Para expressões racionais, onde o denominador abriga pelo menos uma variável, há restrições que impedem a injetividade do relacionamento.

Exemplo 4

Seja a função F: r → R definido por F (x) = 10/x

A função é definida para todos os números reais, exceto 0 quem apresenta uma indeterminação (não pode ser dividida entre zero).

Ao se aproximar de zero à esquerda, a variável dependente leva valores negativos muito grandes e imediatamente após zero, os valores da variável dependente levam grandes figuras positivas.

Esta interrupção faz a expressão F: r → R definido por F (x) = 10/x

Não seja injetivo.

Como visto nos exemplos anteriores, a exclusão de valores no domínio serve para "reparar" essas indeterminações. Zero é excluído do domínio, deixando os conjuntos de conjuntos e chegada definidos da seguinte forma:

R - 0 → R

Onde R - 0 simboliza o real, exceto por um conjunto cujo único elemento é zero.

Dessa maneira, a expressão F: R - 0 → R definido por F (x) = 10/x é injetivo.

 Exemplo 5

Seja a função F: [0 , π ] → R definido por F (x) = sin (x)

No intervalo [0 , π ] A função sinusal varia seus resultados entre zero e um.

Pode servir a você: variável aleatória: conceito, tipos, exemplos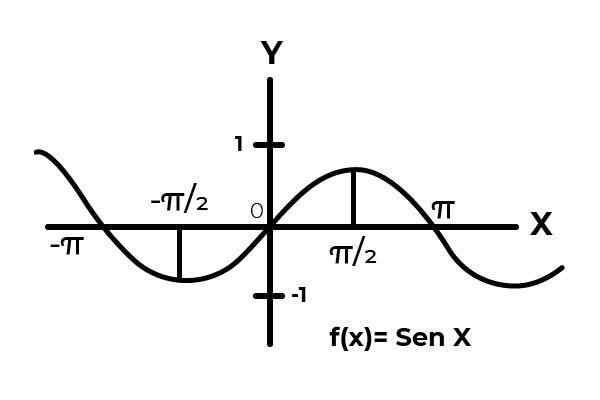Fonte: Autor.

Como pode ser visto nos gráficos. Comece do zero em x = 0 então atingindo um máximo em x = π/2. É depois x = π/2 que os valores começam a ser repetidos, até retornar a zero x = π. Dessa forma, sabe -se que F (x) = sin (x) não é injetivo Para o intervalo [0 , π ] .

Ao estudar os gráficos da função F (x) = sin (x) Os intervalos são observados onde o comportamento da curva se adapta aos critérios de injetividade. Como o intervalo  [[  π/2,3π/2  ]

Onde a função varia os resultados de 1 a -1, sem repetir nenhum valor na variável dependente.

Desta forma, a função F: [  π/2,3π/2  ] → R definido por F (x) = sin (x). É injetivo

Exemplo 6

Verifique se a função F: [0, ∞) → R definido por F (x) = 3x² É injetivo.

Nesta ocasião, o domínio da expressão já está limitado. Observa -se também que os valores variáveis ​​dependentes não são repetidos neste intervalo.

Portanto, pode -se concluir que F: [0, ∞) → R definido por F (x) = 3x²   É injetivo

Exemplo 7

Identificar qual das seguintes funções é

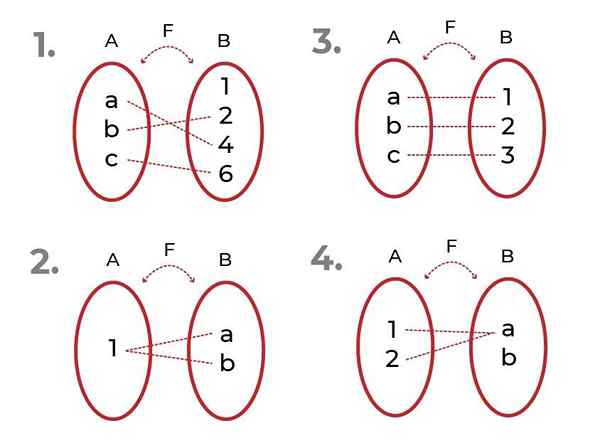Fonte: Autor

1. É injetivo. Os elementos associados do codomínio são únicos para cada valor da variável independente.
2. Não é injetivo. Existem elementos do co -ominium associado a mais de um elemento do conjunto inicial.
3. É injetivo
4. Não é injetivo

Exercícios propostos para aula/casa

Verifique se as seguintes funções são injetivas:

F: [0, ∞) → R definido por F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R definido por F (x) = tan (x)

F: [ -π,π  ] → R definido por F (x) = cos (x + 1)

F: r → R definido pela linha F (x) = 7x + 2

Referências

1. Introdução à lógica e pensamento crítico. Merrilee h. Salmão. Universidade de Pittsburgh
2. Problemas em análise matemática. Piotr Bilar, Alfred Witkowski. Universidade de Wroclaw. Pólo.
3. Elementos da análise abstrata. MÍCHEL O'SEARCOID PhD. Departamento de Matemática. University College Dublin, Beldfield, Dublind 4.
4. Introdução à lógica e à metodologia das ciências dedutivas. Alfred Tarski, Nova York Oxford. imprensa da Universidade de Oxford.
5. Princípios de análise matemática. Enrique Linés Escardó. Editorial reverté s. A 1991. Barcelona Espanha.