Coeficiente de atrito dinâmico ou cinético, exemplos, exercícios

O Fricção dinâmica ou cinético É o que ocorre entre dois corpos em contato quando a superfície de um deles se move em relação à superfície do outro. Por exemplo, em uma caixa que desliza o atrito em uma inclinação é dinâmica e distribuída na superfície de contato do bloco.

A inclinação deve ser grande o suficiente, para que o componente tangencial do peso seja igual ou supere a força de atrito, caso contrário, o bloco que desce acabaria parando para parar.

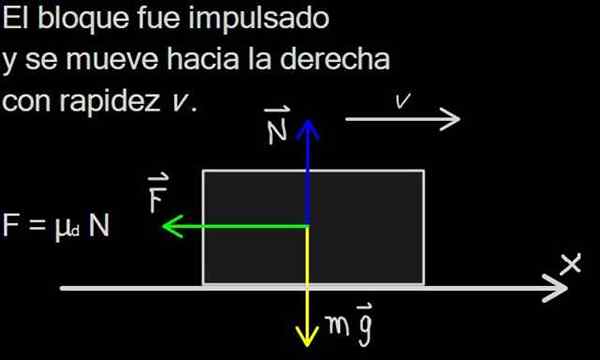
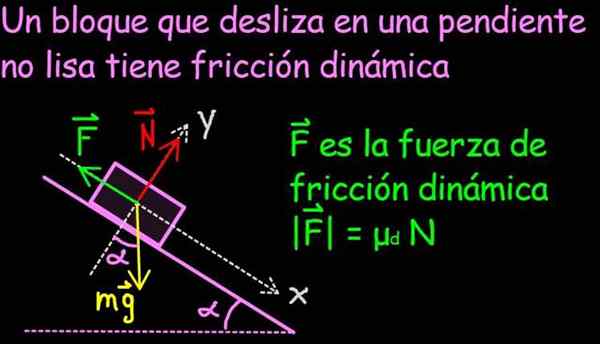figura 1. A força de atrito é distribuída na superfície de contato do bloco, mas no diagrama das forças é representado como uma única força f, fonte: f. Zapata

A força de atrito é de extrema importância na vida cotidiana, pois permite a locomoção de pessoas, animais e veículos. Em uma superfície sem atrito, como a de um sorvete, não é possível iniciar o movimento.

O atrito também permite que nossos carros parem quando estiverem se movendo.

Ao aplicar os freios, as pastilhas de freio são apertadas contra discos de rodas e, graças ao atrito dinâmico, pare a rotação deles. Mas não basta ter bons freios, é necessário que haja força de atrito suficiente entre os pneus e o chão, porque finalmente essa é a força da qual dependemos para que o carro pare.

A humanidade aprendeu a lidar com o atrito por seu benefício. Começou assim usando o atrito entre dois pedaços de madeira seca para fazer fogo.

A natureza também aprendeu a lidar com o atrito a seu favor. Por exemplo, as membranas sinoviais que cobrem os ossos das articulações são uma das superfícies com o menor coeficiente de atrito que existe.

[TOC]

Coeficiente de atrito dinâmico

O primeiro a estudar sistematicamente o movimento de um bloco que desliza em uma superfície plana foi Leonardo da Vinci, mas seus estudos passaram despercebidos.

Pode atendê -lo: Dirac Jordan Atomic Model: características e postulações

Não foi até o século XVII que o físico francês Guillaume Amontons redescobriu as leis do atrito:

Leis de atrito dinâmico

1.- A força de atrito presente em um bloco que desliza em uma superfície plana, sempre se opõe à direção do movimento.

2.- A magnitude da força de atrito dinâmica é proporcional ao aperto ou força normal entre as superfícies do bloco e o plano de suporte.

3.- A constante proporcional é o coeficiente de atrito, estático μ_e No caso de não ter μ de escorregamento e dinâmico_d Quando há. O coeficiente de atrito depende dos materiais das superfícies em contato e do estado de rugosidade.

4.- A força de atrito é independente da aparente área de contato.

5.- Uma vez que o movimento de uma superfície começa em relação ao outro, a força de atrito é constante e não depende da velocidade relativa entre as superfícies.

No caso, não há fricção estática e deslizante é aplicada cuja força é menor ou igual ao coeficiente de atrito estático multiplicado pelo normal.

Figura 2. A força de atrito dinâmico se opõe à direção do movimento e sua magnitude é proporcional à da força normal. A constante de proporcionalidade é o coeficiente de atrito dinâmico. Fonte: f. Zapata.

A última propriedade foi o resultado da contribuição do físico francês Charles Augustin de Coulomb, mais conhecido por sua famosa lei de força entre acusações elétricas específicas.

Essas observações nos levam ao modelo matemático para força de atrito dinâmico F:

F = μ_d N

Onde μ_d É o coeficiente de atrito dinâmico e N é a força normal.

Como determinar o coeficiente de atrito dinâmico?

O coeficiente de atrito dinâmico entre duas superfícies é determinado experimentalmente. Seu valor não depende apenas dos materiais de ambas as superfícies, mas do estado de rugosidade ou polimento que eles têm, bem como sua limpeza.

Pode atendê -lo: ondas mecânicas: características, propriedades, fórmulas, tipos

Uma maneira de determinar é aumentar e deslizar uma caixa conhecida em uma superfície horizontal.

Se a velocidade for conhecida no momento de ser conduzida e a distância percorrida a partir desse momento é medida, é possível conhecer a aceleração de frenagem devido ao atrito dinâmico.

Experimentar 

Neste experimento, a velocidade inicial é medida v e a distância d, Então a aceleração de frenagem é:

A = - v² / 2d

O diagrama das forças é mostrado na Figura 2. A magnitude do peso é a massa m do bloco multiplicada pela aceleração da gravidade G e, como é conhecido, o peso sempre aponta verticalmente para baixo.

N É a força normal devido ao impulso da superfície de suporte e é sempre perpendicular (ou normal) ao plano. O normal existe enquanto as superfícies estão em contato e cessarem assim que as superfícies são separadas.

A força F representa a força de atrito dinâmico. Na verdade, é distribuído na superfície inferior do bloco, mas podemos representá -lo como uma única força F aplicado no centro do bloco.

Como há equilíbrio vertical, a magnitude do normal N É igual ao do peso mg:

N = mg

Na direção horizontal, a força de atrito produz a desaceleração do bloco de massa M de acordo com a segunda lei de Newton:

-F = m a

A força de atrito F aponta para a esquerda, portanto seu componente horizontal é negativo, m é a massa do bloco e a é a aceleração de frenagem.

Havia obtido anteriormente A = - v² / 2d E também o modelo de atrito dinâmico indica que:

F = μD n

Substituindo na equação anterior que você tem:

-μ_d N = - v² / 2d

Levando em consideração que n = mg, você já pode limpar o coeficiente de atrito dinâmico: 

Pode servir você: Modelo Atômico Schrödinger

μ_d = v² / (2d mg)

Tabela de coeficientes de Rocy de alguns materiais

A tabela a seguir mostra os coeficientes de atrito estáticos e dinâmicos para vários materiais. Deve -se notar que sistematicamente o coeficiente de atrito estático é sempre maior que o coeficiente de atrito dinâmico.

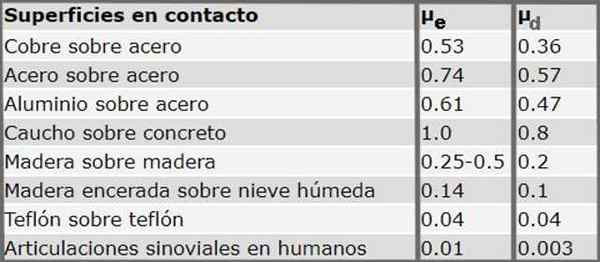Figura 3. Coeficientes de atrito estáticos e dinâmicos para várias superfícies em contato. Fonte: Serway R.PARA. Físico. McGraw-Hill (1992)

Exercícios

- Exercício 1

Um bloco de 2 kg de massa em um piso horizontal é promovido e é liberado. No momento de ser lançado, uma velocidade de 1,5 m/s é registrada. A partir desse momento até o bloco parar por atrito dinâmico 3 m. Determinar o coeficiente de atrito cinético.

Solução

De acordo com a fórmula obtida no exemplo da seção anterior, é o coeficiente dinâmico (ou cinético) é:

μ_d = v² / (2d mg) = 1.52 / (2x3x2 x9.8) = 0,019.

- Exercício 2

Sabendo que o bloco na Figura 1 desce com velocidade constante, que a massa do bloco é de 1 kg e que a inclinação do plano é 30º, determina:

a) o valor do atrito dinâmico

b) o coeficiente de atrito dinâmico entre o bloco e o avião.

Solução

Na Figura 4, a equação do movimento (Segunda Lei de Newton) é mostrada para o problema de um bloco que desce uma inclinação com coeficiente de atrito μ_d  e inclinação α (ver diagrama das forças na Figura 1)

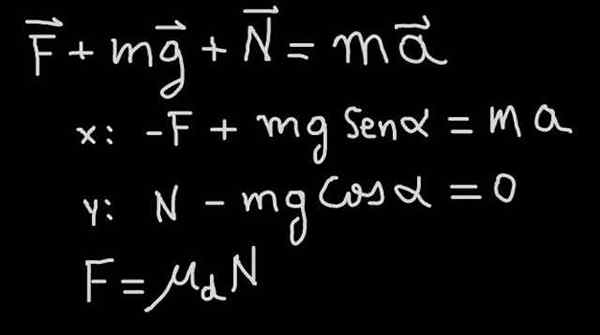Figura 4. A segunda lei de Newton aplicada ao bloco que desliza em uma inclinação com atrito. Fonte: f. Zapata.

Em nosso exercício, somos informados de que o bloco desce com velocidade constante, portanto desce com aceleração a = 0. A partir daí, segue -se que a força de atrito é tal que é igual ao componente tangencial do peso: f = mg sen (α).

No nosso caso M = 1 kg e α = 30º, então a força de atrito f tem um valor de 4,9n.

Por outro lado, a força normal n é a mesma e contrária ao componente perpendicular do peso: n = mg cos (α) = 8,48n .

A partir daí, segue -se que o coeficiente de atrito dinâmico é:

μ_d = F / n = 4,9n / 8.48n = 0,57

Referências

1. Alonso m., Finn e. 1970. Físico. Volume I. Mecânica. Fundo Educacional Inter -Americano.PARA.
2. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
3. Hewitt, p. 2012. Ciência física conceitual. QUINTA EDIÇÃO.
4. Rex, a. 2011. Fundamentos da Física. Pearson. 
5. Serway r. 1992. Físico. McGraw-Hill.
6. Jovem, h. 2015. Física da Universidade com Física Moderna. 14ª ed. Pearson.