Fórmula de frequência absoluta, cálculo, distribuição, exemplo

O Frecuência absoluta É definido como o número de vezes que os mesmos dados são repetidos no conjunto de observações de uma variável numérica. A soma de todas as frequências absolutas é equivalente a totalizar os dados.

Quando há muitos valores de uma variável estatística, é conveniente organizá -los adequadamente para extrair informações sobre seu comportamento. Essas informações são fornecidas por medidas de tendência central e medidas de dispersão.

figura 1. A frequência absoluta de uma observação estatística é a chave para encontrar a tendência que segue o conjunto de dados

Nos cálculos dessas medidas, os dados são representados através da frequência com que aparecem em todas as observações.

O exemplo a seguir mostra como é revelador a frequência absoluta de cada dados. Durante a primeira metade de maio, esses foram os tamanhos dos trajes de coquetel de melhor vendimento, de um armazém de roupas de mulheres bem conhecido:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Quantos vestidos são vendidos em um tamanho específico, por exemplo, tamanho 10? Os proprietários estão interessados ​​em saber fazer pedidos.

Encomendar os dados são mais fáceis de contar, existem exatamente 30 observações no total, do que ordenadas do menor para o mais alto, são assim:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

E agora é evidente que o tamanho 10 é repetido 6 vezes, portanto, sua frequência absoluta é igual a 6. O mesmo procedimento é realizado para descobrir a frequência absoluta dos tamanhos restantes.

[TOC]

Fórmulas

A frequência absoluta, indicada como f_Yo, É igual ao número de vezes como um certo valor x_Yo está dentro do grupo de observações.

Supondo que o total de observações seja de n valores, a soma de todas as frequências absolutas deve ser igual ao referido número:

Pode atendê -lo: Papomudas

∑f_Yo = f₁ + F₂ + F₃ +… F_n = N

Outras frequências

Se cada valor de f_Yo É dividido pelo número total de dados n, você tem o frequência relativa F_r de valor x_Yo:

F_r = f_Yo / N

As frequências relativas são valores entre 0 e 1, porque n é sempre maior do que qualquer f_Yo, Mas a soma deve ser igual a 1.

Multiplicando por 100 para cada valor de f_r você tem a Frequência percentual relativa, cuja soma é 100%:

Frequência percentual relativa = (f_Yo / N) x 100%

Também é importante frequência acumulada F_Yo Até uma certa observação, essa é a soma de todas as frequências absolutas até a referida observação inclusiva:

F_Yo = f₁ + F₂ + F₃ +… F_Yo

Se a frequência acumulada for dividida pelo número total de dados n, você tem o Frequência relativa acumulada, que se multiplicou por 100 resulta no Porcentagem de frequência relativa acumulada.

Como obter a frequência absoluta?

Para encontrar a frequência absoluta de um certo valor que pertence a um conjunto de dados, todos eles são organizados do menos para o maior e o valor é contado.

No exemplo dos tamanhos dos vestidos, a frequência absoluta do tamanho 4 são 3 vestidos, ou seja,₁ = 3. Para o tamanho 6, 4 vestidos foram vendidos: f₂ = 4. No tamanho 8 4 vestidos também foram vendidos, f₃ = 4 e assim por diante.

Tabulação

Os resultados totais podem ser representados em uma tabela que mostra as frequências absolutas de cada um:

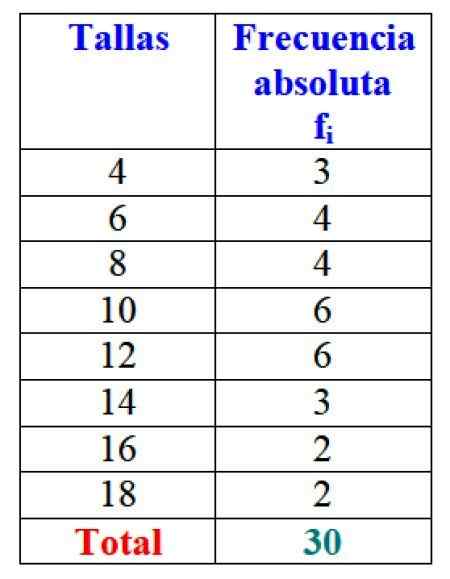Figura 2. Tabela que representa a variável "venda vendida" e as respectivas frequências absolutas. Fonte: f. Zapata.

Obviamente, é vantajoso encomendar as informações e poder acessá -las, em vez de trabalhar com dados soltos.

Importante: Observe que adicionando todos os valores da coluna F_Yo  O número total de dados é sempre obtido. Caso contrário, a contabilidade deve ser revisada, pois há um erro.

Tabela de frequência estendida

A tabela anterior pode ser estendida adicionando os outros tipos de frequência em colunas sucessivas à direita:

Pode servir a você: Homocedasticidade: o que é, importância e exemplos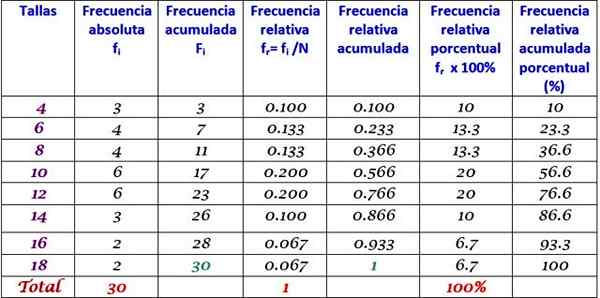

Distribuição de frequência

A distribuição de frequência é o resultado da organização de dados em termos de suas frequências. Ao trabalhar com muitos dados, é conveniente agrupá -los em categorias, intervalos ou classes, cada um com suas respectivas frequências: absoluto, relativo, acumulado e porcentagem.

O objetivo de fazê -los é acessar mais facilmente as informações que os dados contêm, além de interpretá -los adequadamente, o que não é possível quando são apresentados sem ordem.

No exemplo dos tamanhos, os dados não são agrupados, pois não são tamanhos demais e podem ser facilmente manipulados e contados. Variáveis ​​qualitativas também podem ser trabalhadas dessa maneira, mas quando os dados são muito numerosos, elas trabalham melhor as classes nas aulas.

Distribuição de frequência para dados agrupados

Para agrupar os dados em classes de tamanho igual, o seguinte deve ser considerado:

-Tamanho, largura ou amplitude da classe: É a diferença entre o maior valor da classe e o menor.

O tamanho da classe é decidido dividir o intervalo r pelo número de classes a serem consideradas. O intervalo é a diferença entre o valor máximo dos dados e o menor, assim:

Tamanho da classe = alcance / número de classes.

-Limite de classe: intervalo que vai do limite inferior ao limite superior da classe.

-Marca de classe: É o ponto médio do intervalo, que é considerado representativo da classe. É calculado com a semi -limite do limite superior e o limite inferior da classe.

-Número de classes: A fórmula Sturges pode ser usada:

Classes = 1 + 3.322 log n

Onde n é o número de classes. Como geralmente é um número decimal, o seguinte é arredondado.

Exemplo

Uma grande máquina de fábrica está fora de operação, pois tem falhas recorrentes. Os períodos consecutivos de inatividade em minutos, da referida máquina, são registrados abaixo, com um total de 100 dados:

Pode servir a você: probabilidade de frequência: conceito, como é calculado e exemplos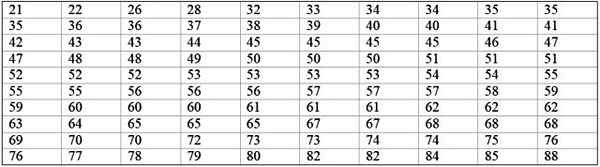

Primeiro, o número de classes é determinado:

Classes = 1 + 3.322 log n = 1 + 3.32 log 100 = 7.64 ≈ 8

Tamanho da classe = intervalo / número de classes = (88-21) / 8 = 8.375

É também um número decimal, por isso leva 9 como tamanho de aula.

A marca de classe é a média entre o limite superior e inferior da classe, por exemplo, para a classe [20-29), há uma marca de:

Marca de classe = (29 + 20) / 2 = 24.5

Prossiga da mesma maneira para encontrar as marcas de classe dos intervalos restantes.

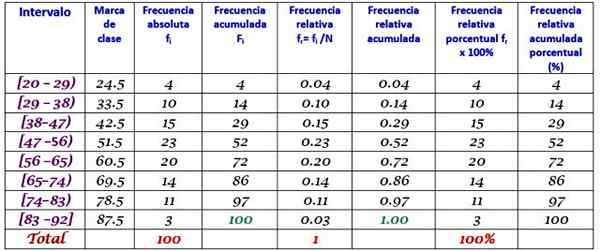
Exercício resolvido

40 jovens indicaram que o tempo em minutos que passou na Internet no domingo passado foi o próximo, ordenado cada vez mais:

0; 12; vinte; 35; 35; 38; 40; Quatro cinco; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

É solicitado para construir a distribuição de frequência desses dados.

Solução

A classificação r do conjunto de n = 40 dados é:

R = 220 - 0 = 220

A aplicação da fórmula Sturges para determinar o número de classes produz o seguinte resultado:

Classes = 1 + 3.322 log n = 1 + 3.32 log 40 = 6.3

Como é decimal, o todo imediato é 7, portanto os dados são agrupados em 7 classes. Cada classe tem uma largura de:

Tamanho da classe = intervalo / número de classes = 220/7 = 31.4

Um valor próximo e redondo é 35, portanto, uma largura de classe de 35 é escolhida.

As marcas de classe são calculadas em média o limite superior e inferior de cada intervalo, por exemplo, para o intervalo [0,35):

Marca de classe = (0+35)/2 = 17.5

Procedemos da mesma maneira com as aulas restantes.

Finalmente, as frequências são calculadas de acordo com o procedimento descrito acima, resultando na seguinte distribuição:

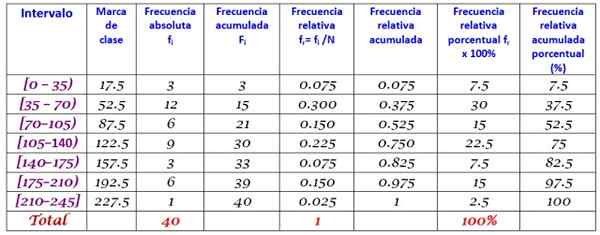
Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
3. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
4. Spiegel, m. 2009. Estatisticas. Série Schaum. 4 ta. Edição. McGraw Hill.
5. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.