Fórmula de frequência acumulada, cálculo, distribuição, exemplos

O frequência acumulada É a soma das frequências absolutas f, da criança a que corresponde a um certo valor da variável. Por sua vez, a frequência absoluta é o número de vezes que uma observação aparece no conjunto de dados.

Obviamente, a variável de estudo deve ser ordenada. E como a frequência acumulada é obtida adicionando as frequências absolutas, verifica -se que a frequência acumulada aos últimos dados deve coincidir com o número total deles. Caso contrário, há um erro nos cálculos.

A frequência acumulada é usada no gerenciamento de dados estatísticos

Em geral, a frequência acumulada é denotada como f_Yo (Ou às vezes n_Yo), para distingui -lo da frequência absoluta f_Yo e é importante adicionar uma coluna para ela na tabela com a qual os dados são organizados, conhecidos como Tabela de frequência.

Dessa maneira, é facilitado, entre outras coisas, manter a conta de quantos dados foram contados até certa observação.

A f_Yo Também é conhecido como Frequência acumulada absoluta. Se você dividir entre os dados totais, você tem o Frequência acumulada relativa, cuja soma final deve ser igual a 1.

[TOC]

Fórmulas

A frequência acumulada de um certo valor de variável x_Yo  É a soma das frequências absolutas f de todos os valores inferiores ou iguais a ele:

F_Yo  = f₁ + F₂ + F₃  +… F_Yo

Ao adicionar todas as frequências absolutas, o número total de dados n é obtido, ou seja::

F₁ + F₂ + F₃ +.. . + F_n = N

A operação anterior é escrita de uma maneira resumida pelo símbolo da soma ∑:

∑ f_Yo = N

Outras frequências acumuladas

As seguintes frequências também podem ser acumuladas:

-Frequência relativa: É obtido dividindo a frequência absoluta f_Yo Entre o total de dados n:

F_r = f_Yo / N

Se as frequências relativas forem adicionadas da criança àquele correspondente a uma certa observação, o Frequência relativa acumulada. O último valor deve ser igual a 1.

-Porcentagem de frequência acumulada acumulada: A frequência relativa acumulada por 100% é multiplicada.

F_% = (f_Yo / N) x 100%

Essas frequências são úteis para descrever o comportamento dos dados, por exemplo, encontrando medidas de tendência central.

Como obter a frequência acumulada?

Para obter a frequência acumulada, é necessário solicitar os dados e organizá -los em uma tabela de frequência. O procedimento é ilustrado na seguinte situação prática:

Pode atendê -lo: sucessão composta

-Em uma loja on -line que vende telefones celulares, o registro de vendas de uma determinada marca do mês de março, os seguintes valores por dia:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

A variável é o Número de telefones vendidos por dia E é quantitativo. Os dados apresentados não são tão fáceis de interpretar, por exemplo, os proprietários da loja podem estar interessados ​​em saber se há alguma tendência, como dias da semana em que as vendas dessa marca são maiores.

Informações como esta e muito mais, podem ser obtidas apresentando os dados de maneira ordenada e especificando as frequências.

Como preencher a tabela de frequência

Para calcular a frequência acumulada, os dados são ordenados:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Em seguida, uma tabela com as seguintes informações é construída:

-A primeira coluna à esquerda com a quantidade de telefones vendidos, entre 0 e 5 e em ordem crescente.

-Segunda coluna: frequência absoluta, que é o número de dias que foram vendidos 0 telefones, 1 telefone, 2 telefones e assim por diante.

-Terceira coluna: a frequência acumulada, consistindo na soma da frequência anterior mais a frequência dos dados a serem considerados.

Esta coluna começa com a primeira coluna da coluna de frequência absoluta, neste caso é 0. Para o próximo valor, isso é adicionado ao anterior. Assim, continuam os últimos dados da frequência acumulada, o que deve coincidir com os dados totais.

Tabela de Frecuência

A tabela a seguir mostra a variável "Número de telefones vendidos em um dia", sua frequência absoluta e o cálculo detalhado de sua frequência acumulada.

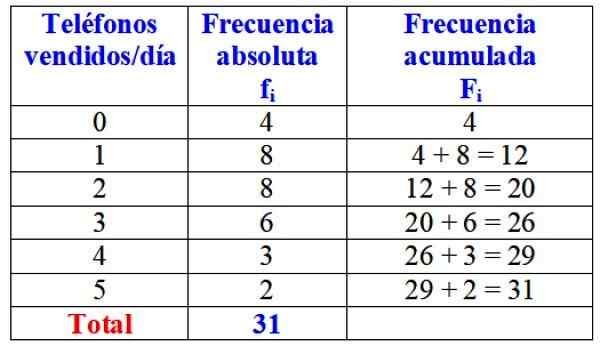Tabela de frequências absolutas e acumuladas para a variável "Telefones vendidos por dia". Fonte: f. Zapata.

À primeira vista, pode -se dizer que a marca em questão é quase sempre vendida um ou dois telefones por dia, uma vez que a frequência mais absoluta é 8 dias, o que corresponde a esses valores da variável. Somente por 4 dias do mês não vendeu um único telefone.

Pode servir a você: Razões trigonométricas: exemplos, exercícios e aplicações

Como observado, é mais fácil examinar a tabela do que os dados soltos originalmente coletados.

Distribuição de frequência acumulada

Uma distribuição de frequência acumulada é uma tabela em que frequências absolutas, frequências acumuladas, frequências relativas acumuladas e frequências percentuais acumuladas estão disponíveis.

Embora a vantagem de organizar os dados em uma tabela como a anterior seja notada, se o número de dados for muito grande, é possível que não seja suficiente organizá -los como mostrado acima, porque se muitas frequências aparecerem, ainda é difícil interpretar.

O problema pode ser remediado construindo um Distribuição de frequência Por intervalos, um procedimento útil quando a variável leva um grande número de valores ou se for uma variável contínua.

Aqui os valores são agrupados em intervalos de igual amplitude, chamado aula. As aulas são caracterizadas por ter:

-Limite de classe: são os valores extremos de cada intervalo, existem dois, o limite superior e o limite inferior. Em geral, o limite superior não pertence ao intervalo, mas aos seguidores imediatos, enquanto o limite inferior pertence.

-Marca de classe: É o ponto médio de cada intervalo e é considerado o valor representativo.

-Largura da classe: É calculado subtraindo o valor do major e o menor (intervalo) e dividido pelo número de classes:

Largura da classe = intervalo / número de classes

Então a elaboração da distribuição de frequência é detalhada.

Exemplo

Este conjunto de dados corresponde a 40 graus de um exame de matemática, na escala de 0 a 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

Uma distribuição de frequência com uma certa quantidade de classes pode ser desenvolvida, por exemplo, 5 classes. Deve -se ter em mente que, ao usar muitas classes, os dados não são fáceis de interpretar e a sensação de realizar o grupo é perdida.

Pode atendê -lo: quanto você precisa adicionar a 3/4 para obter 6/7?

E se pelo contrário eles são agrupados em muito poucos, as informações são diluídas e parte dela é perdida. Tudo depende da quantidade de dados que você tem.

Neste exemplo, é uma boa ideia ter duas pontuações em cada intervalo, uma vez que existem 10 pontuações e 5 classes serão criadas. A classificação é a subtração entre o maior e a menor classificação, sendo a largura da classe:

Largura da classe = (10-0)/5 = 2

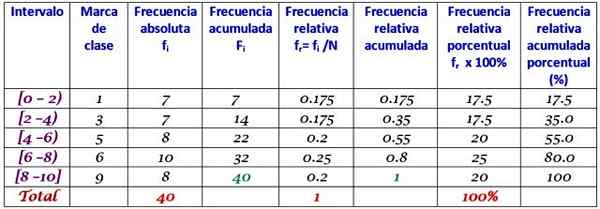
Os intervalos são fechados pela esquerda e aberta à direita (exceto a última), que é simbolizada com colchetes e parênteses, respectivamente. Todos têm a mesma largura, mas não é obrigatório, embora o mais frequente.

Cada intervalo contém uma certa quantidade de elementos ou frequência absoluta, e na coluna seguinte é a frequência acumulada, na qual a soma é transportada. A tabela também mostra a frequência relativa f_r  (Frequência absoluta entre o número total de dados) e a porcentagem de frequência f_r × 100%.

Exercício proposto

Uma empresa fez ligações diárias para seus clientes durante os dois primeiros meses do ano. Os dados são os seguintes:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 14, 16, 9, 6, 10, 12, 13, 17, 14, 14, 26, 7, 12, 24, 7, 7

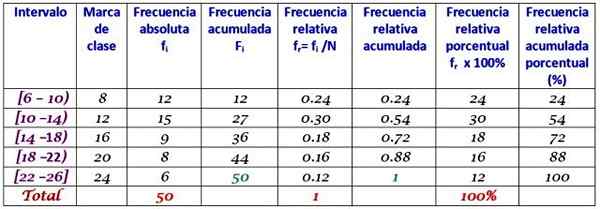
Grupo em 5 classes e construa a tabela com a distribuição de frequência.

Responder

A largura da classe é:

(26-6)/5 = 4

Tente resolvê -lo antes de ver a resposta.

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
3. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
4. Probabilidade e Estatística. Largura do intervalo de classe. Recuperado de: pedroprobabilidade e estadístico.Blogspot.com.
5. Spiegel, m. 2009. Estatisticas. Série Schaum. 4 ta. Edição. McGraw Hill.
6. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.