Fórmulas de energia mecânica, conceito, tipos, exemplos, exercícios

O energia mecânica de um objeto ou sistema é definido como a soma de sua energia potencial e sua energia cinética. Como o nome indica, o sistema adquire energia mecânica graças à ação de forças mecânicas como peso e força elástica.

De acordo com a quantidade de energia mecânica que o corpo possui, também terá a capacidade de realizar um trabalho mecânico.

figura 1. O movimento do carro da montanha de Roller pode ser descrito pela conservação da energia mecânica. Fonte: Pixabay.

A energia - o tipo que é - é uma quantidade escalar, portanto, sem direção e significado. Ser E_m A energia mecânica de um objeto, OU sua energia potencial e K Sua energia cinética, a fórmula para calculá -la é:

E_m = K + u

A unidade no sistema de energia internacional de qualquer tipo é o joule, que é abreviado como j. 1 J é equivalente a 1 n.M (Newton por metro).

Quanto à energia cinética, é calculada da seguinte forma:

K = ½ m.v²

Onde m É a massa do objeto e v Sua velocidade. A energia cinética é sempre uma quantidade positiva, uma vez que a massa e o quadrado da velocidade são. Quanto à energia potencial, se é sobre energia potencial gravitacional, você tem:

U = m.g.h

Aqui m Ainda é a massa, g É a aceleração da gravidade e h É a altura em relação ao nível de referência ou se preferir, o solo.

Agora, se o corpo em questão tiver energia potencial elástica -pode ser uma mola -é porque é comprimido ou talvez alongado. Nesse caso, a energia potencial associada é:

U = ½ kx²

Com k como a mola constante, o que indica como é fácil ou difícil deformá -lo e x A duração da referida deformação.

[TOC]

Conceito e características da energia mecânica

Aprofundando a definição dada antes, a energia mecânica depende da energia associada ao movimento do corpo: energia cinética, além da contribuição da energia potencial, que como dissemos pode ser gravitacional, devido ao peso e ao peso e à posição que ocupa o corpo com Respeito ao solo ou nível de referência.

Vamos ilustrar isso com um exemplo simples: suponha que você tenha uma panela no chão e em repouso. Como ainda está, não tem energia cinética e também está no chão, um lugar de onde não pode cair; Portanto, falta energia potencial gravitacional e sua energia mecânica é 0.

Suponha agora que alguém coloca a panela na beira de um teto ou uma janela, a 3.0 metros de altura. Para isso, a pessoa teve que fazer um trabalho contra a gravidade. O pote agora tem energia potencial gravitacional, pode cair dessa altura e sua energia mecânica não é mais anulada.

Figura 2. Uma panela em cima de uma janela tem energia potencial gravitacional. Fonte: Pixabay.

Nessas circunstâncias, o pote tem E_m = U E essa quantidade depende da altura e peso da panela, como indicado antes.

Digamos que a panela cai porque estava em uma posição precária. À medida que sua velocidade aumenta e com ela sua energia cinética, enquanto a energia potencial gravitacional diminui, porque perde a altura. A energia mecânica a qualquer momento do outono é:

Pode atendê -lo: quais são as magnitudes derivadas?

E_m = U + k = ½ m.v² + m.g.h  

Forças conservadoras e não conservadoras

Quando a panela está em uma certa altura, tem energia potencial gravitacional porque quem a subiu, fez um trabalho contra a gravidade. A magnitude deste trabalho vale o mesmo que aquela que faz a gravidade quando o pote cai Da mesma altura, mas tem o sinal oposto, já que foi feito contra.

O trabalho que forças como gravidade e elasticidade depende apenas da posição inicial e da posição final adquirida pelo objeto. Não importa a trajetória seguida para ir de um para outro, apenas os próprios valores importa. As forças que se comportam dessa maneira são chamadas Forças conservadoras.

E, como são conservadores, eles permitem que o trabalho realizado por eles sejam armazenados como energia potencial na configuração do objeto ou sistema. É por isso que a panela na beira da janela ou teto teve a possibilidade de cair e com ela para desenvolver movimento.

Por outro lado, existem forças cujas obras dependem do caminho seguido pelo objeto em que eles agem. O atrito pertence a esse tipo de forças. Sapatos Solas serão gastos mais quando você passar de um lugar para outro em uma estrada com muitas voltas do que quando você vai para mais um direto.

Forças de atrito fazem um trabalho que diminui a energia cinética dos corpos, porque os diminui. E é por isso que a energia mecânica dos sistemas em que o atrito atende a diminuir.

Parte do trabalho realizado pela força é perdido por calor ou som, por exemplo.

Tipos de energia mecânica

A energia mecânica é, como dissemos, a soma de energia cinética e energia potencial. Agora, a energia potencial pode vir de várias forças conservadoras: peso, força elástica e força eletrostática.

- Energia cinética

A energia cinética é uma quantidade escalar que sempre se torna o movimento. Qualquer partícula ou objeto em movimento tem energia cinética. Um objeto que se move em uma linha reta tem energia cinética de tradução. O mesmo acontece se estiver girando, neste caso, há falar sobre energia cinética rotacional.

Por exemplo, um carro que se move ao longo de uma estrada tem energia cinética. Também uma bola de futebol enquanto se move pela quadra ou a pessoa que caminha às pressas para chegar ao escritório.

- Energia potencial

É sempre possível associar uma função escalar chamada energia potencial a uma força conservadora. Os seguintes são distinguidos:

Energia potencial gravitacional

Aquele que todos os objetos têm em virtude de sua altura em relação ao solo, ou o nível de referência que foi selecionado como tal. Como exemplo, alguém que está em repouso no terraço de um edifício de 10 histórias, tem energia potencial 0 em relação ao solo do terraço, mas não com relação à rua que está 10 andares abaixo.

Energia potencial elástica

Geralmente é armazenado em objetos como ligas e molas, associadas à deformação que eles experimentam ao esticar ou comprimi -las.

Energia potencial eletrostática

É armazenado em um sistema de cargas de eletricidade em equilíbrio, devido à interação eletrostática entre eles. Suponha que haja duas cargas elétricas do mesmo sinal separado a uma pequena distância; Como as cargas elétricas do mesmo sinal são repelidas, espera -se que um agente externo tenha feito trabalho para aproximá -los.

Pode atendê -lo: Circuitos atuais alternados: tipos, aplicações, exemplos

Uma vez posicionado, o sistema consegue armazenar o trabalho que o agente fez para configurá -los, na forma de energia potencial eletrostática.

Conservação de energia mecânica

Voltando ao pote em queda, a energia potencial gravitacional que ele tinha quando estava na beira do telhado é transformada em movimento cinético do movimento. Isso aumenta às custas do primeiro, mas a soma de ambos permanece constante, já que a queda do pote é ativada pela gravidade, que é uma força conservadora.

Existe uma troca entre um tipo de energia e outro, mas a quantidade original é a mesma. Portanto, é válido afirmar que:

Energia mecânica inicial = energia mecânica final

E_M = E_{M final}

Alternativamente:

K_inicial + OU_inicial = K _final + OU_final

Em outras palavras, a energia mecânica não muda e ∆E_m = 0. O símbolo "∆" significa variação ou diferença entre um valor final e um inicial.

Para aplicar corretamente o princípio da conservação da energia mecânica para resolver problemas, é necessário:

-Aplica -se apenas quando as forças que atuam no sistema são conservadoras (gravidade, elástica e eletrostática). Em tal caso: ∆E_m = 0.

-O sistema de estudo deve ser isolado. Não há transferência de energia de forma alguma.

-Se em um problema aparecer, então ∆E_m ≠ 0. Mesmo assim, o problema pode ser resolvido encontrando o trabalho realizado pelas forças conservadoras, uma vez que é a causa da diminuição da energia mecânica.

Dedução da conservação de energia mecânica

Suponha que uma força conservadora age no sistema que faz um trabalho C. Este trabalho causa uma mudança na energia cinética:

W = ∆K (Teorema da energia de trabalho cinético)

É importante observar que o teorema da energia do trabalho cinético é aplicável mesmo no caso de forças não conservadoras.

Por outro lado, o trabalho também é responsável pela mudança de energia potencial e, no caso de uma força conservadora, a mudança na energia potencial é definida como o negativo desse trabalho:

W = -∆U

Combinando essas equações, pois ambas se referem ao trabalho realizado no objeto:

∆K = -∆U 

K_F - K_qualquer = -(u_F - OU_qualquer)

Os subscritos simbolizam "final" e "inicial". Agrupamento:

K_F + OU_F = K_qualquer + OU_qualquer                                                    

Exemplos de energia mecânica

Muitos objetos têm movimentos complexos, nos quais é complicado encontrar expressões para a posição, velocidade e aceleração em função do tempo. Nesses casos, a aplicação do princípio de conservação de energia mecânica é um procedimento mais eficaz do que tentar aplicar as leis de Newton diretamente.

Vejamos alguns exemplos em que a energia mecânica é preservada:

-Um esquiador que desliza ladeira abaixo sobre colinas nevadas, desde que a ausência de atrito seja suposta. Nesse caso, o peso é a força causadora do movimento ao longo da trajetória.

-Carrinhos de montanha russos, É um dos exemplos mais típicos. Aqui também o peso é a força que define movimento e energia mecânica é preservada se não houver atrito.

Pode atendê -lo: energia de ionização

-O pêndulo simples Consiste em uma massa sujeita a uma corda inentendida -não muda o comprimento -que se separa brevemente da vertical e é permitido oscilar. Sabemos que acabará por parar devido ao atrito, mas quando o atrito não é considerado, a energia mecânica também é preservada.

-Um bloco que afeta uma primavera fixado por uma extremidade na parede, tudo em uma mesa muito suave. O bloco comprime a mola, percorre uma certa distância e é disparada na direção oposta, porque a mola se estende. Aqui o bloco adquire sua energia potencial graças ao trabalho que faz a mola nele.

-Primavera e bola: Quando uma mola é compactada por uma bola, este salto. Isso ocorre porque quando a mola é liberada, a energia potencial se torna energia cinética na bola.

-Salto de trampolim: Funciona semelhante a uma primavera, promovendo elasticamente a pessoa que pula nele. Isso faz uso de seu peso ao pular, com o qual deforma o trampolim, mas este, ao retornar à sua posição original, dá o impulso ao jumper.

Figura 3. O trampolim atua como uma primavera, promovendo as pessoas que pulam nela. Fonte: Pixabay.

Exercícios resolvidos

- Exercício 1

Um objeto de massa M = 1 kg é jogado por uma rampa de uma altura de 1 m. Se a rampa estiver extremamente suave, calcule a velocidade do corpo exatamente quando a mola colidir.

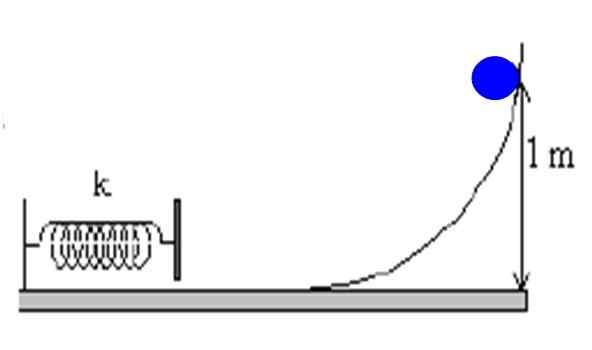Figura 4. Um objeto desce sobre uma rampa sem atrito e comprime uma mola que é presa à parede. Fonte: f. Zapata.

Solução

A declaração relata que a rampa é suave, o que significa que a única força que age no corpo é o seu peso, uma força conservadora. Assim, é indicado para aplicar a conservação da energia mecânica entre qualquer ponto da trajetória.

Considere os pontos marcados na Figura 5: A, B e C.

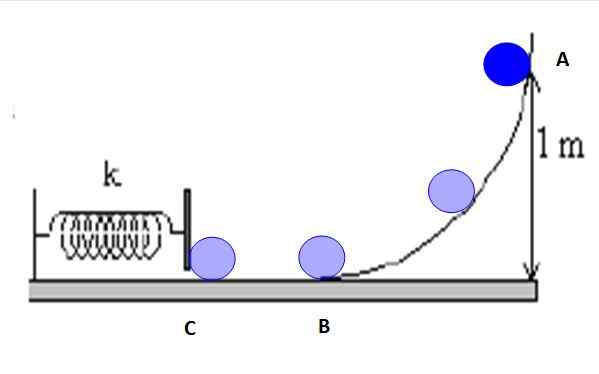Figura 5. O caminho que segue o objeto é o atrito e a energia mecânica é preservada entre qualquer par de pontos. Fonte: f. Zapata.

É possível estabelecer a conservação da energia entre A e B, B e C ou A e C, ou qualquer um dos pontos intermediários na rampa. Por exemplo, entre A e C, você tem:

Energia mecânica em A = energia mecânica em C

E_MA = E_Mc

K_PARA + OU_PARA = K_C + OU_C

½ m.v_PARA² + m.g.h_PARA = ½ m V_C² + m.g.h_C

Como é liberado do ponto A, a velocidade v_PARA = 0, por outro lado H_C = 0. Além disso, a massa é cancelada, porque é um fator comum. Então:

g.h_PARA = ½ v_C²

v_C²= 2 g.h_PARA

- Exercício 2

Encontre a compressão máxima que a mola do exercício resolveu 1 experimentará, se a constante elástica do mesmo for 200 n/m.

Solução

A constante elástica da mola indica a força a ser aplicada para deformar uma unidade de comprimento. Como a constante desta primavera vale k = 200 n/m, isso indica que 200 n é necessário para comprimir ou esticá -lo 1 m.

Ser x A distância que o objeto comprime a mola antes de parar no ponto D:

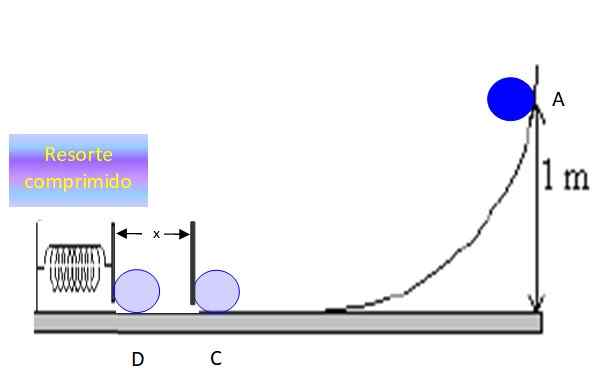Figura 6. O objeto comprime a mola e a distância e para momentaneamente. Fonte: f. Zapata.

A conservação da energia entre os pontos C e D estabelece que:

K_C + OU_C = K_D + OU_D

No ponto C, não possui energia potencial gravitacional, pois sua altura é 0, mas possui energia cinética. Em D ele parou completamente, portanto, k_D = 0, mas você tem à disposição a energia potencial da mola compactada u_D.

A conservação da energia mecânica permanece:

K_C = U_D

½ mv_C² = ½ kx²

 

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Figueroa, d. 2005. Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
3. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson.
4. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.
5. Wikipedia. Energia mecânica.Recuperado de: é.Wikipedia.org.