Propriedades do Enegon, como fazer um Enegon, exemplos

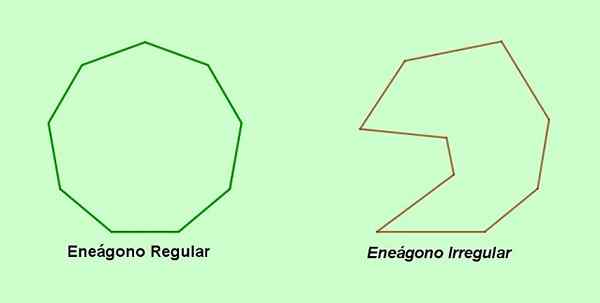
A Enegon É um polígono de nove lados e nove vértices, que podem ser regulares ou não. A denominação do Enegon vem do grego e consiste nas palavras gregas ENNEA (nove e Gonon (ângulo).

Um nome alternativo para o polígono de nove anos é uma palavra não -palavra que vem de latim não (nove e Gonon (vértice). Por outro Enegon irregular. Se pelo contrário, os nove lados e os nove ângulos do Enegon são iguais, então é um Enegon regular.

figura 1. Enegon regular e Enegon irregular. (Elaboração própria)

[TOC]

Propriedades do Enegon

Para um polígono de n lados, a soma de seus ângulos internos é:

(N - 2) * 180º

No Enegon, seria n = 9, então a soma de seus ângulos internos é:

SA = (9 - 2) * 180º = 7 * 180º = 1260º

Em qualquer polígono, o número de diagonais é:

D = n (n - 3) / 2 e no caso de Enegon, como n = 9, você precisa d = 27.

Enegon regular

No Enegon ou nonagon comum.

É então necessário medir os ângulos internos de um Enegon é 1260º / 9 = 140º.

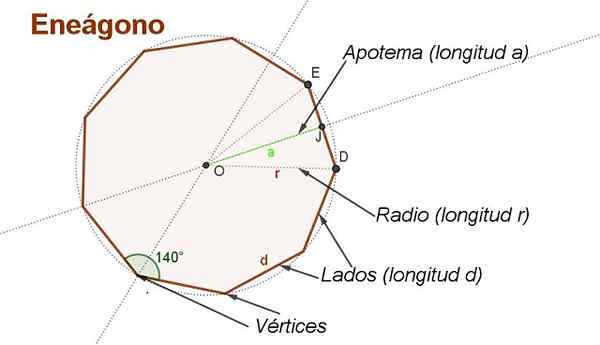Figura 2. Apotem, rádio, laterais, ângulos e vértices de um Enegon regular. (Elaboração própria)

Para deduzir a fórmula da área de um Enegon regular do lado d É conveniente fazer algumas construções auxiliares, como as mostradas na Figura 2.

O centro é QUALQUER Desenhando os mediatrices de dois lados adjacentes. Centro QUALQUER Equidista dos vértices.

Um raio de comprimento r É o segmento que vai do centro QUALQUER Em um vértice do Enegon. Os rádios são mostrados na Figura 2 OD e OE de comprimento r.

Pode atendê -lo: simetria

O apothem é o segmento que vai do centro para o ponto médio de um lado do Enegon. Por exemplo OJ É um apotem cuja duração é para.

Área de um lado conhecido e apothem

Consideramos o triângulo TRIBUTO Da Figura 2. A área deste triângulo é o produto de sua base DE por altura OJ Dividido por 2:

Área TRIBUTO = (De * oj) / 2 = (D * a) / 2

Como existem 9 triângulos da mesma área no Enegon, conclui -se que a área do mesmo é:

Área Enegon = (9/2) (D * A)

Área de um Enegon conhecido

Se apenas o comprimento do Enegon for conhecido, é necessário encontrar o comprimento do gotamento para poder aplicar a fórmula da seção anterior.

Consideramos o triângulo Oje Retângulo em J (Veja a Figura 2). Se a proporção trigonométrica de torque for aplicada, é obtido:

então(∡OEJ) = OJ / Por exemplo.

O ângulo ∡oej = 140º / 2 = 70º, para ser EO Bissetor do ângulo interno do Enegon.

Por outro lado, OJ É o gotamento de comprimento para.

Então como J É um ponto médio de Ed Segue que Ex = d/2.

Substituir os valores acima na relação da tangente é:

Tan (70º) = A / (d / 2).

Agora limpamos o comprimento do apothem:

A = (d/2) Bronzeado (70º).

O resultado anterior é substituído na fórmula da área para obter:

Área Enegon = (9/2) (d * a) = (9/2)( D * (D/2) Bronzeado (70º))

Finalmente, existe a fórmula que permite que a área regular do Enegon seja obtida se apenas o comprimento for conhecido d de seus lados:

Área Enegon = (9/4) D² Tan (70º) = 6.1818 D²

Perímetro do Enegon regular conhecia seu lado

O perímetro de um polígono é a soma de seus lados. No caso do Enegon, como todos e cada um dos lados, ele mede um comprimento d, Seu perímetro será a soma de nove vezes d, quer dizer:

Pode atendê -lo: equações polinomiais

Perímetro = 9 d

Perímetro do Enegon conhecia seu rádio

Considerando o triângulo Oje Retângulo em J (Veja a Figura 2), a razão trigonométrica Cosen é aplicada:

cos (∡OEJ) = Por exemplo / Oe = (d / 2) / r

Onde você está obtido:

D = 2r cos (70º)

Substituindo esse resultado, a fórmula do perímetro é obtida em função do raio Enegon:

Perímetro = 9 d = 18 r cos (70º) = 6.1564 r

Como fazer um Enegon regular

1- Para construir um Enegon regular, com regra e bússola, é baseado na circunferência c que circunscreve o Enegon. (Veja a Figura 3)

2- Duas linhas perpendiculares são desenhadas através do centro ou circunferência. Então os cruzamentos A e B de uma das linhas são marcados com a circunferência.

3- com a bússola, fazendo o centro da interceptação b e a abertura igual ao raio bo.

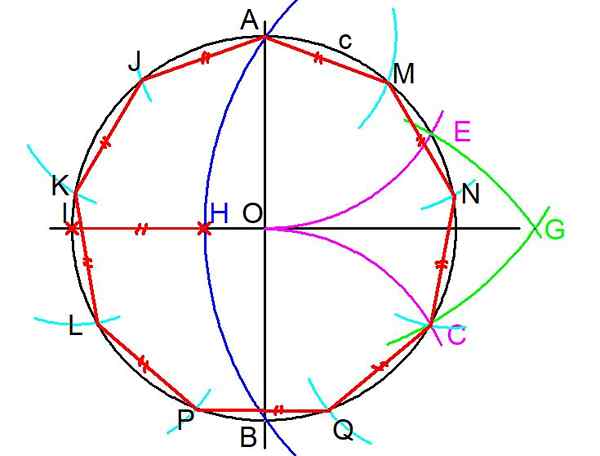Figura 3. Passos para construir um Enegon regular. (Elaboração própria)

4- A etapa anterior é repetida, mas fazendo um centro em A e Radio AO é desenhado um arco que intercepta para a circunferência C no ponto E.

5- Com a abertura e o centro de CA em um arco de circunferência é desenhado. Da mesma forma com a abertura be e o centro B, outro arco é desenhado. A interseção desses dois arcos é marcada como um g.

6- Fazendo o centro em G e com a abertura de GA é desenhada que intercepta o eixo secundário (horizontal neste caso) no ponto H. A interseção do eixo secundário está marcada com a circunferência original C como eu.

7- O comprimento do segmento IH é igual ao comprimento d na lateral do Enegon.

8- Com uma bússola aberta IH = D Os arcos centrais são sucessivamente atraídos para a Radio AJ, Centro J Radio AK, KL Radio KL e Centro L Radio LP.

Pode servir a você: Transformações lineares: Propriedades, quais são o uso, tipos, exemplos

9- Da mesma forma, a partir de A e do lado direito, os arcos de rádio ih = D são desenhados na circunferência original C Pontos M, N, C e Q.

10- Finalmente os segmentos AJ, JK, KL, LP, AM, MN, NC, CQ e finalmente PB são desenhados.

Deve -se notar que o método de construção não é totalmente exato, pois pode ser verificado que o último lado PB é 0,7% mais longo que os outros lados. Até o momento, não se sabe um método de construção e construção de bússolas que é 100% preciso.

Exemplos

Alguns exemplos resolvidos serão abordados abaixo.

Exemplo 1

Você quer construir um Enegon regular cujos lados medem 2 cm. Que rádio deve a circunferência que circunscreva, para que, ao aplicar a construção descrita anteriormente, o resultado desejado seja obtido?

Solução:

Em uma seção anterior, a fórmula que relaciona o raio r da circunferência circunscrita com o dégon regular foi deduzida:

D = 2r cos (70º)

Limpando r da expressão anterior que temos:

R = d / (2 cos (70º)) = 1.4619 * d

Substituindo o valor d = 2 cm na fórmula anterior, um raio de 2,92 cm é obtido.

Exemplo 2

Quanto é a área de um lado regular de 2 cm?

Solução:

Para responder a essa pergunta, você deve se referir à fórmula, demonstrada anteriormente, que permite encontrar a área de um Enegon conhecida o comprimento D de lado:

Área Enegon = (9/4) D² Tan (70º) = 6.1818 D²

Substituindo D por seu valor de 2 cm na fórmula anterior é obtida:

Área Enegon = 24,72 cm

Referências

1. C. E. PARA. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
2. Campos, f., CERECEDO, f. J. (2014). Matemática 2. Grupo editorial da Patria.
3. Libertado, k. (2007). Descubra polígonos. Companhia de Educação de Benchmark.
4. Hendrik, v. (2013). Polígonos generalizados. Birkhäuser.
5. Iger. (s.F.). Matemática Primeiro Semestre Tacaná. Iger.
6. Jr. Geometria. (2014). Polígonos. Lulu Press, Inc.
7. Miller, Heeren e Hornsby. (2006). Matemática: Raciocínio e Aplicações (Décima Edição). Pearson Education.
8. Patiño, m. (2006). Matemática 5. Editorial Progreso.