Distribuições discretas
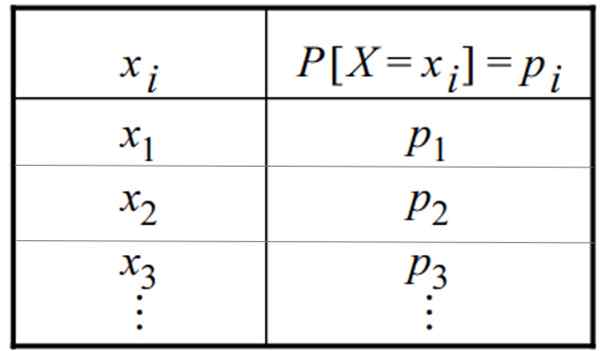
- 2786
- 458
- Ernesto Bruen
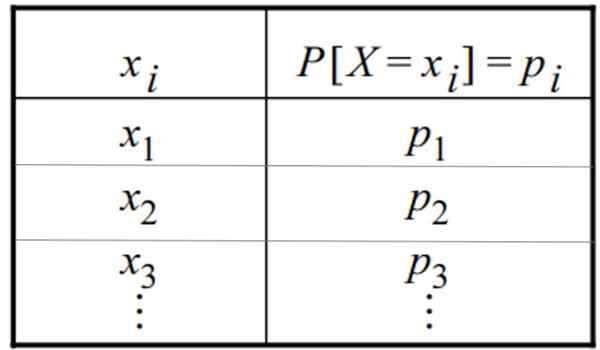 Tabela de uma distribuição de probabilidade discreta. Fonte: f. Zapata
Tabela de uma distribuição de probabilidade discreta. Fonte: f. Zapata O que é uma distribuição discreta?
A distribuição discreta de probabilidades é uma função f (xYo) que atribui a cada valor de uma variável discreta: x1, x2, x3,... xYo, uma certa ocorrência de ocorrência p (x = xYo). Esta função também é conhecida como "função de massa de probabilidade".
A distribuição de probabilidade discreta pode ser dada na forma de uma tabela ou gráficos. Uma tabela tem essa forma geral, na qual a variável aparece em uma coluna e sua respectiva probabilidade no outro:
As funções de massa de probabilidade compartilham as seguintes características gerais:
- A probabilidade pYo de qualquer evento XYo É entre 0 e 1, sendo até alguns desses valores limitados: 0 ≤ x ≤ 1.
- P (x = xYo) = pYo Basta tomar valores positivos, portanto: p (x = xYo) ≥ 0.
- É verdade que ∑ p (xYo) = 1 para todos os valores possíveis de x.
Uma distribuição de probabilidades descreve o comportamento de uma população, descrita por seus parâmetros: a média μ, a variação σ2 e o desvio padrão s = σ σ2.
Em seguida, as distribuições discretas mais notáveis são descritas brevemente:
Distribuição uniforme
É a distribuição mais simples discreta de todos. Nele, a variável pode levar valores discretos "n": x1, x2, x3,... xYo, Tudo com a mesma probabilidade. Nesse caso, a distribuição é dada por:
Distribuição binomial
Aplica -se a experiências com apenas dois resultados possíveis e mutuamente exclusivos, que geralmente são chamados de "sucesso" e "fracasso", indicado como E e F, respectivamente,. O fato de um evento ser chamado de "sucesso", não significa necessariamente que é uma coisa boa, é uma designação arbitrária.
A probabilidade de sucesso p (e) nos ensaios de "n" é indicada como p e a de falha p (f) como q = 1 - p.
Se "X" representa um certo número de sucessos nos ensaios independentes "n", é verdade que: 0 ≤ x ≤ n. E a probabilidade de ocorrência p (x) do evento é calculada através da seguinte fórmula:
Pode atendê -lo: centímetros quadrados a metros quadrados (cm² a m²)Onde x = 0, 1, 2, 3 ..., n e o símbolo (!) significa "fatorial":
x! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1
0! = 1
Distribuição de veneno
Nesta distribuição, a variável aleatória x indica quantas vezes um evento ocorre em algum intervalo, o que pode ser de tempo, distância ou outro. As ocorrências do evento são aleatórias, independentes e são distribuídas uniformemente ao longo do intervalo em questão.
Uma vez essas condições, a probabilidade, que depende da média de μ ocorrências e do número de Euler ou número "e", são calculadas por:
As chances de eventos com esta distribuição são pequenas, por isso é chamado de "lei de casos raros".
Abordagem de distribuição binomial
A distribuição de Poisson serve como uma abordagem da distribuição binomial quando N é grande (n≥ 100) e P é pequeno (np ≤ 10). Nesse caso, a média μ é calculada como:
μ = n ∙ p
Distribuição hipergeométrica
É usado quando as probabilidades não são independentes, ou seja, depois de realizar o experimento, as condições não são as mesmas novamente. É o que acontece ao extrair amostras sem substituição de uma população, então a distribuição binomial não pode mais ser usada.
Se a população consistir em dois tipos de objetos diferentes de e B, e em objetos aleatórios e sem substituição, a probabilidade de obter x objetos do tipo A são:
Onde A e B são as respectivas quantidades de objetos de cada tipo, presentes na população.
No entanto, se a população for muito grande, mesmo que não haja substituição, é difícil para o mesmo elemento ser selecionado mais de uma.
Pode servir a você: diferença de cubos: fórmulas, equações, exemplos, exercíciosExemplos
Lançamentos de moedas
Co -launches são exemplos muito ilustrativos:
-O lançamento de uma moeda honesta e obtenha um rosto. Sabe -se que 1 face tem uma probabilidade de sair e a cruz (0 face), a mesma. A distribuição é mostrada nesta tabela:
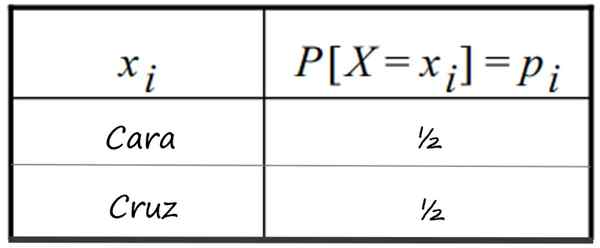 Tabela de distribuição de probabilidade discreta que segue o lançamento de 1 moeda honesta. Fonte: f. Zapata
Tabela de distribuição de probabilidade discreta que segue o lançamento de 1 moeda honesta. Fonte: f. Zapata -A foto simultânea de dois moedas honestas e possíveis faces números que podem ser obtidos.
 Tabela de distribuição de probabilidade discreta que segue o lançamento de duas moedas honestas, com o objetivo de obter qualquer face ou não. Fonte: f. Zapata
Tabela de distribuição de probabilidade discreta que segue o lançamento de duas moedas honestas, com o objetivo de obter qualquer face ou não. Fonte: f. Zapata Variáveis com distribuição uniforme
-A seleção de um número inteiro que é par ou ímpar: cada um é probabilidade igual a ½ de ser escolhido dentro do conjunto de números inteiros.
-O lançamento de um dado honesto. Nesse caso, existem 6 rostos numerados e cada um tem a mesma probabilidade de sair: 1/6.
-A seleção de um tópico para fazer um exame, escolhido entre n questões, se todos eles forem igualmente prováveis.
Variáveis com distribuição binomial
-Número de rostos que saem lançando uma moeda honesta.
-De uma população de 250 famílias, o número dessas que têm 2 filhos.
-A quantidade de pau -madeiras que sobrevivem, depois de um jardineiro 20 rosales em um jardim.
-De um estudo com 50 pacientes, o número deles que apresentou uma reação negativa a um medicamento.
-O número de alunos aprovados em um exame de probabilidades, de um grupo composto por 100 alunos.
Variáveis com distribuição de Poisson
-Número de chamadas por minuto para Central de Atendimento De uma empresa.
-Número de grandes terremotos por ano para uma área geográfica específica.
-O número de tornados que afetaram uma determinada região durante o último ano.
-Número de árvores infectadas com um fungo, por hectare quadrado da floresta.
Variáveis com distribuição hipergeométrica
-Sucessos de números ou combinações vencedoras no jogo.
Pode atendê -lo: vetores simultâneos: características, exemplos e exercícios-Seleção de um certo número de mulheres ou machos em uma amostra de n peixe de um aquário.
Exercícios resolvidos
Exercício 1
Um estudo determinou que, por adultos selecionados aleatoriamente que têm smartphones, 54% deles os usam em sala de aula ou reuniões. Você deseja encontrar a probabilidade de que, selecionando aleatoriamente 8 pessoas com smartphone, exatamente 6 delas as usem em sala de aula ou reuniões.
Solução
Este experimento concorda com um experimento binomial, pois o resultado é binário: uma pessoa leva o telefone em sala de aula ou não o retira. O fato de a pessoa usar o telefone em sala de aula pode ser chamada de sucesso e uma falha se não o fizer (antes de ser explicado que essa escolha é completamente arbitrária).
Nesse caso: p = 0.54 e Q = 1- 0.54 = 0.46.
Como 8 pessoas são selecionadas aleatoriamente, então n = 8 e o valor de x é 6, portanto, os valores necessários estão disponíveis para substituí -los na fórmula de distribuição binomial:
Exercício 2
Por um ano recente, uma clínica registrou 4221 nascimentos. Com esses dados exclusivos, determine a probabilidade de que haja 15 nascimentos em 1 dia. Este evento é raro?
Solução
A distribuição de Poisson é usada, pois é solicitada para determinar a probabilidade de ocorrência de um evento que ocorre em um intervalo de tempo. Nesse caso, a variável é a quantidade de nascimentos e o intervalo é de 1 dia.
A fórmula de distribuição de Poisson precisa do nascimento médio por dia, que é facilmente calculado:
Portanto, a probabilidade de x = 15 nascimentos/dia é:
O resultado pode ser expresso em termos de porcentagem para clareza: 6.42% provavelmente que, a qualquer dia, exatamente 15 nascimentos ocorrem. O evento é improvável, embora em nenhum caso seja impossível.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)