Distribuição de frequência como fazer uma tabela, exemplo, exercício

A Distribuição de frequência Nas estatísticas, refere -se à tendência que segue os dados organizados em grupos, categorias ou classes, quando cada um recebe um número chamado frequência, o que indica quantos dados existem em cada grupo. 

Como regra, observa -se que essas frequências são distribuídas em torno de um grupo central: aquele com o maior número de dados.

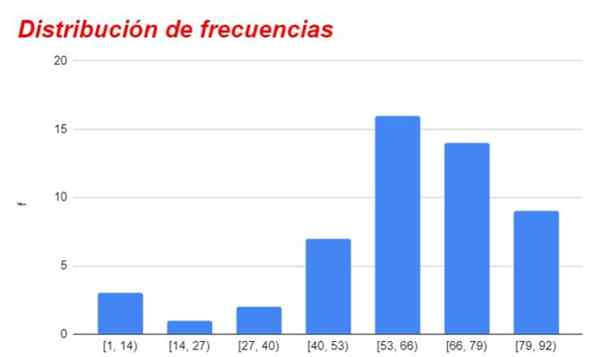
figura 1. Gráfico de distribuição de frequência obtido de sua tabela correspondente. Fonte: f. Zapata.

Grupos acima ou abaixo da referida categoria central diminuem gradualmente sua frequência, sendo muito pequeno ou insignificante para as categorias mais distantes da categoria com uma frequência mais alta.

A maneira de conhecer a distribuição de frequência de um conjunto de dados consiste primeiro na criação das categorias e depois fazer a tabela de frequência. A representação visual da tabela de frequência é chamada de histograma.

[TOC]

Tipos de frequência

Existem vários tipos de frequências:

1.- Frecuência absoluta: É o mais básico e, a partir dela, os outros são construídos. Simplesmente consiste no número total de dados correspondentes a uma categoria.

2.- Frequência relativa: É a frequência absoluta de cada categoria dividida pelo número total de dados.

3.- Frequência percentual: É a mesma frequência relativa, mas multiplicada por cento, indicando a porcentagem de valores que aparecem em cada categoria.

4.- Frequência acumulada: É a soma das frequências absolutas das categorias inferiores ou iguais à categoria que está sendo considerada. 

5.- Frequência percentual acumulada: É a soma das frequências percentuais das categorias inferiores ou iguais à categoria que está sendo observada.

Etapas para fazer uma tabela de distribuição de frequência

Existem várias etapas a serem seguidas para construir uma tabela de distribuição de frequência.

Em primeiro lugar, os dados devem de uma árvore, etc.

Pode atendê -lo: quais são os divisores de 30? (Explicação)

Passo 1

Identifique o valor mínimo Xmin e o valor máximo Xmax No conjunto de dados x.

Passo 2

Calcule o intervalo R, que é definido como a diferença entre o valor máximo menor o valor mínimo: r = xmax - xmin.

etapa 3

Determine o número k de intervalos ou classes, que podem ser pré -estabelecidos. O número k determinará o número de linhas que a tabela de frequência terá.

Passo 4

Caso o número de intervalos k Não é dado anteriormente, deve ser estabelecido de acordo com as seguintes diretrizes: o menor número de categorias recomendadas é 5, mas pode ser maior, caso em que é preferível escolher um número ímpar.

Etapa 5

Há uma fórmula chamada Regra de ressecros Isso nos dá o número de intervalos k recomendado para um conjunto que consiste em N dados:

K = [1 + 3.3222idrol n]

Como o resultado dentro do suporte certamente será um número real, o suporte indica que deve ser arredondado para o número inteiro ímpar mais próximo para obter um valor inteiro de k.

Etapa 6

A amplitude é calculada PARA de cada intervalo (classes ou categorias), levando o quociente entre o intervalo R e o número de intervalos k: A = r/k. Se os dados originais forem números inteiros, o número inteiro mais próximo será arredondado, caso contrário, seu valor real será deixado.

Etapa 7

Determinar os limites inferiores e superiores de cada intervalo ou classe. O primeiro intervalo, ou a classe mais baixa, tem como limite inferior o menor dos dados originais, ou seja, li = xmin e como o limite superior do valor mínimo mais a amplitude do intervalo, este é LS = xmin + A. 

Etapa 8

Os intervalos sucessivos são: 

[[Xmin, xmin + a), [ Xmin + a, xmin + 2⋅A), ... [ Xmin + (k-1) a, xmin + k⋅a).

Pode atendê -lo: operações combinadas

Etapa 9

A marca da classe XC é determinada para cada intervalo, usando a seguinte fórmula: Xc = (ls - li) / 2 + li.

Etapa 10

O cabeçalho da tabela de frequência é colocado, que consiste em uma linha com os seguintes rótulos: classes, marca de classe XC, frequência F, frequência relativa F (ou porcentagem de frequência F%) e frequência acumulada F (ou frequência percentual acumulada F%).

O que teremos a seguir é o seguinte:

Primeira coluna da tabela de frequência: contém os intervalos ou classes em que os dados foram divididos.

Segunda coluna: contém a marca de classe (ou ponto intermediário) de cada subinterval.

Terceira coluna: Contém a frequência absoluta f de cada classe ou categoria.

Quarta e quinta coluna: Os valores correspondentes à frequência relativa (ou porcentagem) e à frequência acumulada F (ou porcentagem acumulada) são colocados.

Exemplo de construção de mesa

Os dados a seguir correspondem às respostas precisas de 100 perguntas aplicadas a um grupo de 52 alunos:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.

Seguiremos as etapas para construir a tabela de frequência:

1.- Valores mínimos e máximos xmin = 1, xmax = 89.

2.- O intervalo é: r = 89 - 1 = 88

3.- Determinação do número de intervalos de acordo com o Regra de ressecros: K = [1 + 3.3222⋅Log 52] = [6,70] = 7.

4.- Cálculo da largura dos intervalos: a = r / k = 88/7 = 12,57 ≈ 13.

5.- Os intervalos são: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- As marcas de classe de cada intervalo são determinadas: 8, 21, 34, 47, 60, 73 e 86.

7.- A tabela é feita:

Pode atendê -lo: ângulos conjugados internos e externos: exemplos, exercícios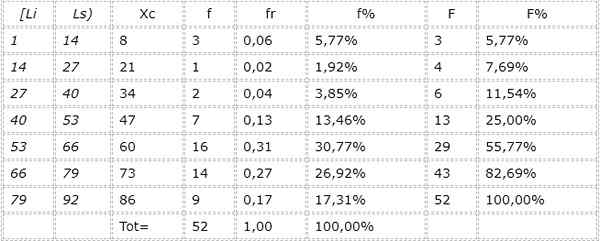

O gráfico das frequências para diferentes intervalos ou categorias é mostrado na Figura 1.

Exercício resolvido

Um professor registra a porcentagem de objetivos alcançados no assunto da física para cada aluno. No entanto, a qualificação para cada aluno, embora dependa da porcentagem de objetivos alcançados, é rígida para certas categorias anteriormente estabelecidas nos regulamentos de estudos universitários.

Vejamos um caso específico: em uma seção de física, você tem a porcentagem de objetivos alcançados para cada um dos 52 alunos: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

Neste exemplo, as categorias ou classes correspondem à qualificação final atribuída de acordo com a porcentagem x dos objetivos alcançados:

1.- Muito pobre: ​​1 ≤ x < 30

2.- Pobre: ​​30 ≤ x < 50

3.- Chega: 50 ≤ x < 70

4.- Bem: 70 ≤ x < 85

5.- Excelente: 85 ≤ x ≤ 100

Para fazer a tabela de frequência, os dados são ordenados do menos para o maior e informa quantos dados correspondem a cada categoria, que será a qualificação que o aluno obterá no assunto da física:

1.- Muito pobre: ​​4 alunos.

2.- Pobre: ​​6 alunos.

3.- Chega: 20 alunos.

4.- Bem: 17 alunos.

5.- Excelente: 5 alunos.

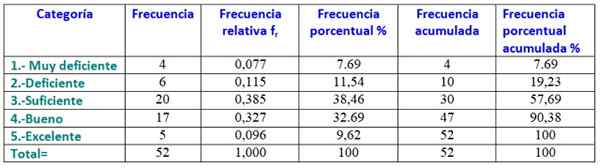
Abaixo está o histograma de notas, construído a partir da tabela anterior:

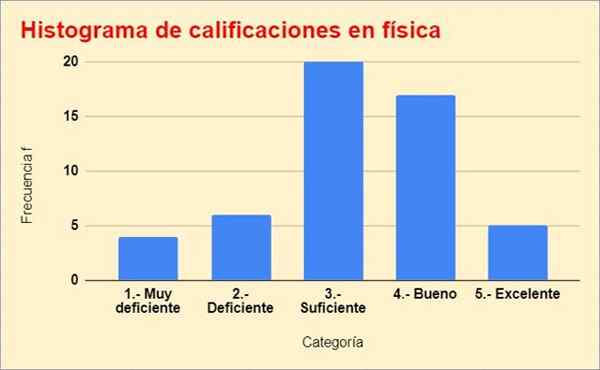Figura 2. Gráfico de distribuição de frequência do exercício resolvido. Fonte: f. Zapata.

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
3. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
4. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
5. Spiegel, m. 2009. Estatisticas. Série Schaum. 4 ta. Edição. McGraw Hill.
6. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.