Fourier Series Aplicações, Exemplos e Exercícios resolvidos

As Séries de Fourier Eles consistem em uma soma de termos infinitos, que consistem em funções harmônicas, seio e cosseno, cujo argumento é um todo fundamental de uma frequência fundamental.

As funções seno e cosseno são multiplicadas por coeficientes de valores, de modo que a soma seja idêntica a uma função com o período t igual a duas vezes Pi (2π) dividido pela frequência angular fundamental ω ω ω.

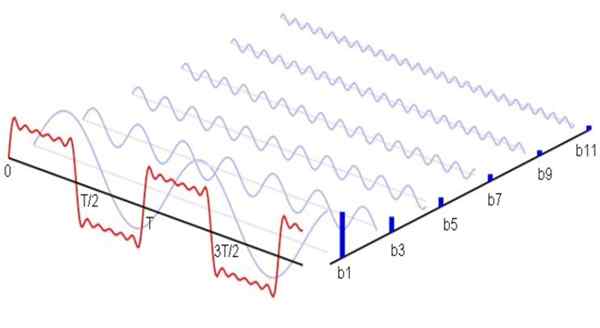
figura 1. Aqui estão (em azul) os primeiros harmônicos não -nulos da série Fourier, correspondendo a um sinal de forma de onda quadrado. A soma que esses harmônicos dão origem ao sinal vermelho. Fonte: Wikimedia Commons.

Matematicamente, seria expresso da seguinte maneira: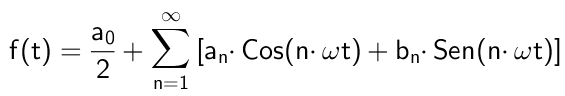

Onde Ω É a frequência fundamental, que está relacionada ao período T da função f (t) Através do relacionamento: 

Ω = 2π / t

Por ser período periódico T, a função f (t) atende a esta condição:

f (t) = f (t + k t)

Onde k É um número inteiro e os coeficientes para₀ , para_n e B_n Eles são chamados de Coeficientes de Fourier.

[TOC]

Importância e usos da série Fourier

O nome da série Fourier se deve ao fato de seu descobridor ser o matemático francês.

Essa descoberta foi fundamental para a matemática, pois se uma equação diferencial tem uma solução harmônica específica, é possível alcançar a solução geral por meio da sobreposição ou soma da mesma.

Os coeficientes de Fourier de uma função periódica, também chamados sinal, Eles são o espectro do mesmo.

Portanto, o espectro é o conjunto de frequências que compõem um sinal caracterizado pela amplitude de cada frequência, que corresponde aos valores dos coeficientes de Fourier.

Sistemas de compressão de sinal ou formas de onda de áudio e vídeo, na parte traseira um número significativamente menor de bits do que o sinal digitalizado original.

A série de Fourier de um sinal é como sua impressão digital, no sentido de que, conhecido os coeficientes que compensam, você sempre pode saber qual sinal eles pertencem.

Embora o uso da série de Fourier, ou sua forma mais geral, o transformada de Fourier, Como método de compactação de sinal que ele é conhecido há algum tempo, seu uso na prática teve que esperar por processadores numéricos rapidamente o suficiente, o que permitia que os sinais fossem compactados e descomprimidos em "tempo real".

Pode atendê -lo: variáveis ​​estatísticas

Exemplo da série Fourier 

Em seguida, um exemplo de função f (t) e sua série de Fourier.

A função é:

 f (t) = 0 sim 0 ≤ t  < π y 1 si π ≤  t   < 2π

E tem sua série de Fourier correspondente dada por:

f (t) = ½ - 2/π⋅se (t) - 2/(3π) ⋅se (3t) - 2/(5π) ⋅sen (5t) - 2/(7π) ⋅sen (7t) -…

A figura a seguir mostra a função e a soma parcial da série Fourier:

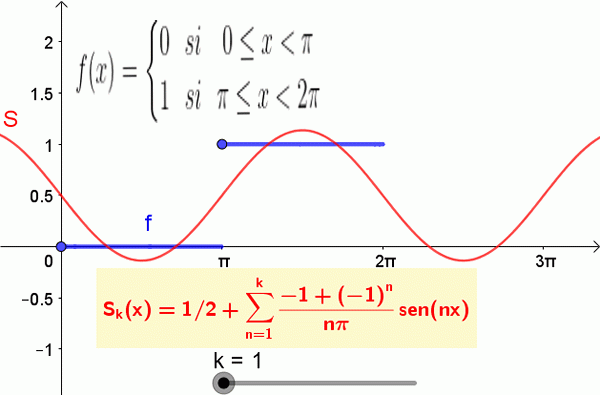Figura 2. Os 19 primeiros termos da soma de Fourier correspondentes à função de etapa são mostrados. Fonte: f. Zapata.

Determinação de coeficientes

Abaixo está como determinar os coeficientes de Fourier:

Suponha que a função seja f (x) definida em um intervalo que passa de t_Yo para t_Yo + T, onde o capital será o período da função. Então sua série de Fourier é:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n ω t) +…

.. .+ b₁ sin (ω t) +b₂ sin (2 Ω t) +… +b_n Sin (n ω t) +..

Cálculo do termo independente

Para encontrar o termo independente, integramos os dois membros da igualdade no intervalo de definição da função:

[T_Yo , t_Yo+ T]

Portanto:

Mesmo_n ∫Cos (n ω t) dt +…

.. .+ b₁ ∫sen (ω t) dt +b₂ ∫sen (2 Ω t) dt +… +b_n ∫sen (n ω t) dt +…

Aqui o símbolo ∫ significa integral definido de t_Yo para t_Yo + T.

A integral do primeiro termo é t, que, quando avaliada em seus resultados de limite superior:

t_Yo + T

Ao subtrair o limite inferior t_Yo, em t.

Todos os outros termos são 0, porque são funções cosseno ou sinusal avaliadas em um período completo, como mostramos abaixo:

∫Cos (nω t) dt = (1/ nω) ∫Cos (nω t) d (nω t)

Lembre -se de que o símbolo ∫ significa integração entre t_Yo para t_Yo + T. 

Para fazer a integração dos termos que possuem cosseno ou mama, faremos a seguinte mudança de variável:

x = ω (t - t_Yo)

Portanto, o diferencial x, dx é igual ao diferencial d (ωt).

Portanto, a integral a ser realizada é:

Como n é um número inteiro, a integral definida sempre dará zero. O mesmo vale para a função seno.

Portanto, a integral definida avaliada em um período completo de todos os termos contêm. 

Pode atendê -lo: divisões em que o resíduo é 300

Portanto, conclui -se que o termo A₀ é calculado da seguinte forma:

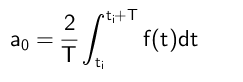
Cálculo de coeficientes para

Para calcular os coeficientes que se multiplicam às funções cosseno, ambos os membros da igualdade devem ser multiplicados:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n ω t) +…

.. .+ b₁ sin (ω t) +b₂ sin (2 Ω t) +… +b_n Sin (n ω t) +..

Pela função cosseno avaliada no harmônico correspondente e depois a integral definida em um período completo para ambos os membros é aplicado. 

Por exemplo, para calcular_m Ambos os membros são multiplicados por COS (MωT):

f (t) cos (m ω t) = a₀/2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 ω t) cos (m ω t) +… + para_n Cos (n ω t) cos (m ω t) +…

.. .+ b₁ sin (ω t) cos (m ω t) +b₂ sin (2 Ω t) cos (m ω t) +… +b_n Sin (n ω t) cos (m ω t) +..

Em seguida, integrar -se a um período completo, isto é, no intervalo que vai de t_Yo para t_Yo + T.

A integral do termo contendo A₀ é cancelada, porque M é um número inteiro e a função cosseno está sendo integrada a um período completo. 

Integrais que contêm o produto cos (n ω t) cos (m ω t) também são anulados sempre que n ≠ m. Somente no caso de n = m ter a integral:

Todos os termos que têm um seio multiplicado de cosseno, ou seja, aqueles que são multiplicados pelos coeficientes de B, como contendo integrais do tipo Sen (n ω t) cos (M ω t) são cancelados quando a integral definida é feita em um completo período. 

Daqui concluiu que:

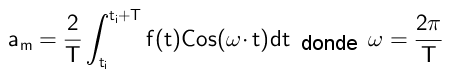
Cálculo dos coeficientes B's

Para encontrar os coeficientes de B, um procedimento semelhante é aplicado, mas desta vez os dois membros da função correspondem à série Fourier são multiplicados pela função Sen (M ω t).

Pelas mesmas razões já explicadas para o caso em que o único termo que não é anulado após a integração em um período completo é aquele em que:

n = m

E onde a integral de [sen (m ω t)] aparece]², aquele integrado em um período completo resulta em π.

Pode servir a você: Função homográfica: Como representar graficamente, exercícios resolvidos

Dessa forma, os coeficientes de B são calculados de acordo com a seguinte fórmula:

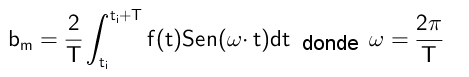
Exercícios

- Exercício 1

Fazer o cálculo explícito dos coeficientes da função

 f (t) = 0 sim 0 ≤ t  < π y 1 si π ≤  t   < 2π

Solução

Primeiro, identificamos o período t dessa função como 2π, portanto a frequência fundamental ω = 2π/ t neste exemplo é igual à unidade, ou seja:

Ω = 1

A função é definida no intervalo [0, 2π], portanto todas as integrações serão realizadas no referido intervalo. 

Então o termo independente é calculado da seguinte maneira:

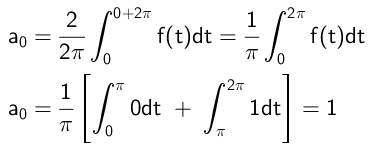
Os coeficientes que se multiplicam às funções cosseno são calculados dessa maneira:

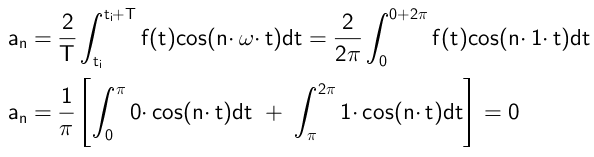
Como pode ser visto, todos os coeficientes são nulos, o que acontecerá desde que a função f (t) seja estranha.

Da mesma forma, os coeficientes de B serão calculados da seguinte forma:

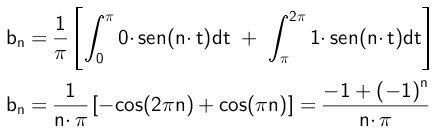
- Exercício 2

Encontre os coeficientes da função correspondente à Figura 1, que é:

f (t) = -1 sim 0≤ t

Solução 

À medida que a função leva os valores entre -1 e +1, podemos intuir que o termo independente seja nulo, no entanto, calculamos explicitamente:

Devido ao fato de a função ter uma simetria estranha, todos os coeficientes que multiplicam os termos harmônicos com a função cosseno devem ser nulos. Nós verificamos abaixo:

Finalmente, encontraremos os coeficientes do B que multiplicam os termos harmônicos que contêm a função sinusal:

Onde todos os termos de B com subscrito podem ser notados são 0. Os primeiros termos ímpares são:

b₁= -4/(π); b₃= -4/(3π); b₅= -4/(5π); b₇= -4/(7π) e B₉= -4/(9π)

https: // youtu.Be/737yagwszya

Referências

1. Amerror, i. 2013. Dominando a transformação discreta de Fourier em um, duas ou várias dimensões: armadilhas e artefatos. Springer Science & Business Media.
2. Briggs, w. novecentos e noventa e cinco. O Manual do DFT: um proprietário para a transformação discreta de Fourier. Siam.
3. Chu, e. 2008. Transformações discretas e contínuas de Fourier: análise, aplicações e algoritmos rápidos. CRC Press.
4. Guoan BI, Yonghong Zeng. 2012. Transformações e algoritmos rápidos para análise e representações de sinal. Springer Science & Business Media.
5. Sundararajan, d. 2003. Processamento de sinal digital: teoria e prática.Scientific World. 
6. Wikipedia. Séries de Fourier. Recuperado de: é.Wikipedia.com