Dinâmica de exemplos de sistema de partículas, exercícios

O Dinâmica de um sistema de partículas Consiste na aplicação das leis de Newton do movimento a um conjunto de partículas, que podem ser discretas (as partículas podem ser contadas) ou para fazer parte de um objeto estendido, neste caso o sistema é contínuo.

Para explicar o movimento de um sistema de partículas, é inconveniente analisar cada um separadamente e ver o que as forças agem nele. Em vez disso, um ponto representativo do conjunto é definido, chamado Centro de massa.

A descrição do movimento do centro de massa oferece um panorama muito bem -sucedido do movimento global do conjunto, também permite aplicar as leis de Newton análogas a quando o objeto é considerado como uma partícula sem dimensões.

Este último modelo, chamado Modelo de partículas, É bom descrever traduções e também quando não é necessário considerar as dimensões do objeto. Mas os objetos comuns são de tamanho e, se eles também têm movimento de rotação, é necessário levar em consideração os pontos nos quais as forças são aplicadas.

[TOC]

Exemplos

A terra e a lua

Ilustração Terra e Lua

Um conjunto de partículas discretas m₁, m₂, m₃... Isso eventualmente se move com relação à origem de um sistema de coordenadas, devido a alguma força resultante que age sobre eles é um bom exemplo de sistema de partículas.

A Terra pode ser considerada como uma partícula e a lua outra, depois ambos constituem um sistema de 2 partículas sob a ação da força da gravidade do sol.

Objetos estendidos

Uma pessoa, um animal ou qualquer objeto do meio ambiente, também pode ser considerada como um sistema de partículas, apenas que eles são tão pequenos, que não se pode contar um por um. Este é um sistema contínuo, mas, levando em consideração certas considerações, seu tratamento é o mesmo que para um sistema discreto.

Pode atendê -lo: qual é a entalpia do treinamento? (Com exercícios)

Aqui estão os detalhes.

O centro de massa de um sistema de partículas

Para iniciar o estudo de um sistema de partículas, você precisa encontrar o centro de massa (CM), que é o ponto em que toda a massa do sistema está concentrada.

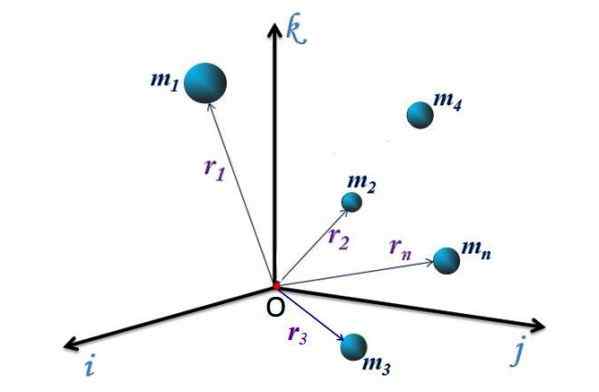
figura 1. Um sistema de partículas no sistema de referência XYZ. Fonte: f. Zapata.

Para o sistema discreto da Figura 1, com n partículas, cada uma tem um vetor de posição direcionado do sistema de origem ou coordenadas para o ponto p (x, y, z) onde a partícula é. Esses vetores são denotados como r₁, r₂, r₃.. r_n.

As coordenadas CM são calculadas pelas seguintes equações:

Onde cada uma das massas do conjunto é representada como m₁, m₂, m₃... m_n. Observe que a soma ∑ m_Yo É equivalente à massa total m do conjunto. Se o sistema for contínuo, os resumos serão substituídos por integrais.

Cada um dos endereços perpendiculares é representado pelos vetores da unidade Yo, J e k, Portanto, o vetor da posição CM, denotado r_Cm, Pode ser expresso por:

r_Cm = x_Cm Yo + e_Cm J + z_Cm k

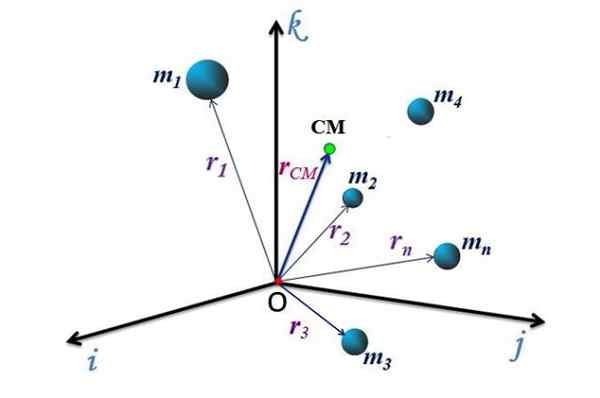Figura 2. Localização do centro de massa de um sistema de partículas. Fonte: f. Zapata.

Movimento cm

Uma vez que a localização do centro de massa é conhecida, as equações conhecidas do movimento são aplicadas. A velocidade do CM é a primeira derivada da posição em relação ao tempo:

Nesse caso, o sistema tem uma quantidade total de movimento P que é calculado como o produto da massa total do sistema e a velocidade do centro de massa:

Pode servir a você: trajetória física: características, tipos, exemplos e exercícios

P = M ∙v_Cm

Como alternativa, a quantidade total de sistema do sistema pode ser calculada diretamente:

P = m₁v₁ + m₂v₂ + m₃v₃ +.. . = ∑ m_Yo v_Yo

Enquanto a aceleração do CM é a velocidade derivada:

Força em cm

As forças que atuam em um sistema de partículas podem ser:

• Forças internas, devido a interações entre as mesmas partículas.
• Forças externas, causadas por agentes externos ao sistema.

Como as forças internas são apresentadas por pares, da mesma magnitude e direção, mas os sentidos opostos, de acordo com a terceira lei de Newton, é cumprido que:

∑ F_int = 0

Portanto, as forças internas não alteram o movimento do todo, mas são muito importantes para determinar a energia interna.

Se o sistema estiver isolado e não houver forças externas, de acordo com a primeira lei de Newton, o centro de massa está em repouso ou se move com movimento retilíneo uniforme. Caso contrário, o centro de massa experimenta uma aceleração dada por:

∑ F_ext = M ∙para_Cm

Onde m é a massa total do sistema. A equação anterior pode ser escrita assim:

E isso significa que a força externa é equivalente à variação temporária na quantidade de movimento, outra maneira de expressar a segunda lei de Newton e a mesma usada pelo famoso físico inglês em seu livro Princípio.

Exercício resolvido

O centro de massa de um sistema de 2 partículas está no eixo x em um certo momento, na posição x = 2.0 me movendo com velocidade 5.0 m/s na mesma direção e positivamente. Se uma das partículas está na origem e a outra, de massa 0.1 kg, está em repouso em x = 8.0 m, calcule:

Pode servir a você: diamagnetismo: materiais, aplicações, exemplos

a) a massa da partícula que está na origem.

b) quantidade de movimento do sistema

c) Que velocidade é a partícula que está na origem?

Solução para

Da equação para a posição do centro de massa:

r_Cm = x_Cm Yo + e_Cm J + z_Cm K = 2.0 m Yo

Como o CM possui apenas uma coordenada X, é usada a primeira equação trio previamente dada:

As coordenadas agora são substituídas, se a partícula for indicada na origem como o número 1 e o outro como o número 2, os dados numéricos são:

x₁ = 0 m, x₂ = 8.0 m, m₂ = 0.1 kg, x_Cm = 2.0 m

Ficando:

= 0.3kg

Solução b

A quantidade de movimento do sistema é calculada por:

P = M ∙v_Cm

A massa total m é igual a:

M = 0.3 kg + 0.1 kg = 0.4 kg

Portanto:

P = 0.4 kg ∙ 5.0 m/s Yo = 2 kg.EM Yo

Solução c

Da equação para P de um sistema de dois partidos, ele limpa v₁, Como os outros dados são conhecidos, porque a declaração diz que a partícula 2 está em repouso, portanto:

v₂ = 0 

E P É simplesmente como:

P = m₁v₁

v₁ = P / m₁ = 2 kg.EM Yo / 0.3kg = 6.67 m/s Yo

Referências

1. Universidade Duke. Sistemas de partículas. Recuperado de: webhome.Phy.Duque.Edu.
2. Rex, a. 2011. Fundamentos da Física. Pearson.
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. Pearson.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
5. Tipler, p. (2006) Física para ciência e tecnologia. 5ª ed. Volume 1. Editorial revertido.