Exemplos de dados agrupados e exercício resolvido

O dados agrupados Eles são aqueles que classificaram em categorias ou classes, tendo como critério sua frequência. Isso é feito com o objetivo de simplificar o gerenciamento de grandes quantidades de dados e estabelecer suas tendências.

Uma vez organizado nessas classes para suas frequências, os dados compõem um Distribuição de frequência, a partir do qual as informações de utilidade são extraídas por meio de suas características.

figura 1. Com os dados agrupados, você pode criar gráficos e calcular parâmetros estatísticos que descrevem tendências. Fonte: Pixabay.

Em seguida, veremos um exemplo simples de dados agrupados:

Suponha que a estatura de 100 estudantes do sexo feminino, selecionada entre todos os cursos de física básica de uma universidade, seja medida e os seguintes resultados são obtidos:

Os resultados obtidos foram divididos em 5 classes, que aparecem na coluna esquerda.

A primeira turma, entre 155 e 159 cm, tem 6 alunos, a segunda classe de 160 - 164 cm tem 14 alunos, a terceira classe de 165 a 169 cm é a da maior número de membros: 47. Em seguida, siga a turma de 170-174 cm com 28 alunos e, finalmente, o de 175 a 179 cm com apenas 5.

O número de membros de cada classe é precisamente o frequência qualquer Frecuência absoluta E ao adicionar todos eles, os dados totais são obtidos, que neste exemplo são 100.

[TOC]

Características de distribuição de frequência

Frequência

Como vimos, a frequência é o número de vezes que um fato é repetido. E para facilitar os cálculos das propriedades de distribuição, como média e variação, as seguintes quantidades são definidas:

-Frequência acumulada: É obtido adicionando a frequência de uma classe com a frequência acumulada anterior. A primeira de todas as frequências coincide com a do intervalo em questão, e o último é o número total de dados.

-Frequência relativa: É calculado dividindo a frequência absoluta de cada classe pelo número total de dados. E se multiplicar por 100, você tem a porcentagem de frequência porcentagem.

Pode atendê -lo: funções vetoriais

-Frequência relativa acumulada: É a soma das frequências relativas de cada classe com o acumulado anterior. O último das frequências relativas acumuladas deve ser igual a 1.

Para o nosso exemplo, as frequências são assim:

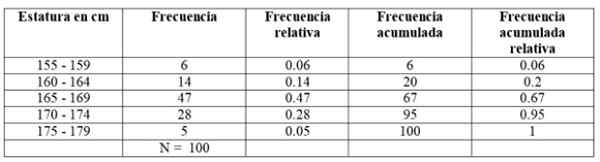
Limites

Os valores extremos de cada classe ou intervalo são chamados Limites de classe. Como podemos ver, cada classe tem um limite inferior e um maior. Por exemplo, a primeira classe do estudo sobre as estaturas tem um limite inferior a 155 cm e um maior que 159 cm.

Este exemplo tem limites que são claramente definidos, no entanto, é possível.

Fronteiras

A altura é uma variável contínua, portanto pode ser considerada que a primeira aula começa em 154.5 cm, já que, arredondando esse valor para o número inteiro mais próximo, 155 cm é obtido.

Esta classe abrange todos os valores de até 159.5 cm, porque a partir disso, as estaturas são arredondadas para 160.0 cm. Uma estatura de 159.7 cm já pertencem à próxima aula.

As fronteiras de classe real deste exemplo são, em CM:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplitude

A amplitude de uma classe é obtida subtraindo as fronteiras. Para o primeiro intervalo do nosso exemplo, você tem 159.5 - 154.5 cm = 5 cm.

O leitor pode verificar se, para os outros intervalos do exemplo, a amplitude também resulta de 5 cm. No entanto, é digno de nota que as distribuições podem ser construídas com intervalos de diferentes amplitude.

Pode atendê -lo: Regra T: Características, para que sejam, exemplos

Marca de classe

É o ponto médio do intervalo e é obtido pela média entre o limite superior e o limite inferior.

Para o nosso exemplo, a marca de primeira classe é (155 + 159)/2 = 157 cm. O leitor pode verificar se as marcas de classe restantes são: 162, 167, 172 e 177 cm.

Determinar marcas de classe é importante, pois são necessárias para encontrar a média aritmética e a variação da distribuição.

Medidas de tendência central e dispersão para dados agrupados

As medidas de tendência central mais usadas são médias, medianas e moda e descrevem precisamente a tendência dos dados a serem agrupados em torno de um certo valor central.

Metade

É uma das principais medidas de tendência central. Nos dados agrupados, a média aritmética pode ser calculada usando a fórmula:

 Onde:

-X é a média

-F_Yo é a frequência da classe

-m_Yo É a marca de classe

-G é o número de classes

-n é o número total de dados

Mediana

Para a mediana, você deve identificar o intervalo em que a observação N/2 está localizada. Em nosso exemplo, essa observação é o número 50, porque há um total de 100 dados. Esta observação está no intervalo 165-169 cm.

Então você deve interpolar para encontrar o valor numérico que corresponde a essa observação, para a qual a fórmula é usada:

Onde:

-C = largura do intervalo onde a mediana está localizada

-B_M = A borda inferior do intervalo ao qual a mediana pertence

-F_m = quantidade de observações contidas no intervalo mediano

-N/2 = metade dos dados totais

-F_BM = Número total de observações antes do intervalo médio

Moda

Para moda, a classe modal é identificada, a que contém a maioria das observações, cuja marca de classe é conhecida.

Pode servir você: pirâmide hexagonal

Variação e desvio padrão

Variação e desvio padrão são medidas de dispersão. Se denotarmos a variação com S² E para o desvio padrão, que é a raiz quadrada da variação como s, para dados agrupados que teremos respectivamente:

E

Exercício resolvido

Para a distribuição da estatura dos estudantes universitários propostos no início, calcule os valores de:

a) média

b) Médio

c) moda

d) Variação e desvio padrão.

Figura 2. Quando se trata de muitos valores, como as estaturas de um grande grupo de estudantes, é preferível agrupar os dados nas aulas. Fonte: Pixabay.

Solução para

Vamos construir a tabela a seguir para facilitar os cálculos:

Através da expressão para o grupo médio agrupado acima:

Substituindo valores e executando a soma diretamente:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Solução b

O intervalo ao qual a mediana pertence é de 165-169 cm, porque é o intervalo com mais frequência.

Vamos identificar cada um desses valores no exemplo, com a ajuda da Tabela 2:

C = 5 cm (consulte a seção de amplitude)

B_M = 164.5 cm

F_m = 47

N/2 = 100/2 = 50

F_BM = 20

Substituindo na fórmula:

Solução c

O intervalo contido na maioria das observações é de 165-169 cm, cuja marca de classe é de 167 cm.

Solução d

Expandimos a tabela anterior adicionando duas colunas adicionais:

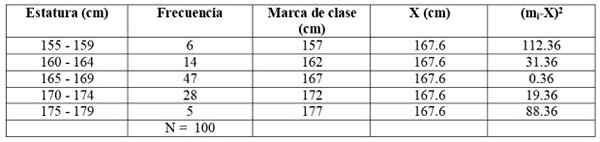
Aplicamos a fórmula:

E desenvolvemos a soma:

s² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Portanto:

S = √21.35 cm² = 4.6 cm

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
3. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
4. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
5. Spiegel, m. 2009. Estatisticas. Série Schaum. 4 ta. Edição. McGraw Hill.
6. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.