Distribuição do qui-quadrado (χ²), como é calculado, exemplos

A prova Chi quadrado qualquer ji-quadrado (χ², Onde χ é a letra grega chamada "chi") é usada para determinar o comportamento de uma determinada variável e também quando você quer saber se duas ou mais variáveis ​​são estatisticamente independentes.

Para verificar o comportamento de uma variável, o teste a ser chamado Teste de ajuste quadrado de chi. Saber se duas ou mais variáveis ​​são estatisticamente independentes do teste Quadrado de Independência, também chamado de contingência.

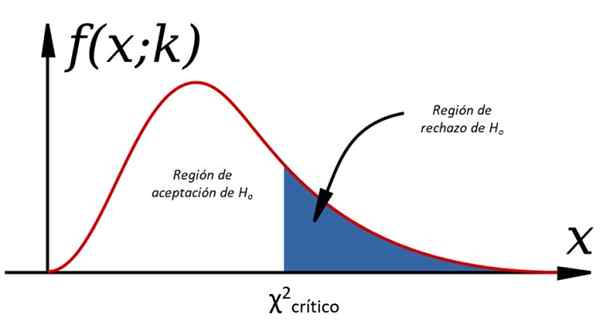
figura 1. Testes de hipótese via Chi Cuadrado

Essas evidências fazem parte da teoria estatística das decisões, nas quais uma população é estudada e as decisões são tomadas sobre isso, analisando uma ou várias amostras extraídas dele. Para isso, é necessário fazer certas suposições sobre as variáveis, chamadas hipótese, que pode ou não ter certeza.

Existem alguns testes para contrastar essas conjecturas e determinar quais são válidas, dentro de uma certa margem de confiança, incluindo o teste do qui-quadrado, que pode ser aplicado para comparar duas e a maioria das populações.

Como veremos, dois tipos de hipótese sobre algum parâmetro populacional em duas amostras são geralmente considerados: a hipótese nula, chamada h_qualquer (As amostras são independentes) e a hipótese alternativa, indicada como H₁, (As amostras estão correlacionadas) o que é contrário a isso.

[TOC]

Quando o teste do qui-quadrado é usado?

O teste quadrado do Chi se aplica a variáveis ​​que descrevem qualidades, como sexo, status civil, grupo sanguíneo, cor dos olhos e preferências de vários tipos.

O teste foi projetado quando desejado:

-Verifique se uma distribuição é apropriada para descrever uma variável, que é chamada ajuste bondade. Através do teste quadrado do Chi, você pode saber se há diferenças significativas entre a distribuição teórica selecionada e a distribuição de frequência observada.

-Saiba se duas variáveis ​​x e y são independentes do ponto de vista estatístico. Isso é conhecido como Teste de independência.

Como se aplica a variáveis ​​qualitativas ou categóricas, o teste de Chi Square é amplamente utilizado em ciências sociais, administração e medicina.

Condições para aplicá -lo

Existem dois requisitos importantes para aplicá -lo corretamente:

Pode atendê -lo: qual é a relação entre a área de Rhombus e o retângulo?

-Os dados devem ser agrupados em frequências.

-A amostra deve ser grande o suficiente para tornar a distribuição quadrada do Chi válida, caso contrário, seu valor é superestimado e gera a rejeição da hipótese nula quando não deve ser assim.

A regra geral é que, se nos dados agrupados uma frequência com valor menor que 5 aparecer, ele não é usado. Se houver mais de uma frequência menor que 5, eles devem ser combinados em um para obter uma frequência com valor numérico maior que 5.

Distribuição quadrada do chi

χ² É uma distribuição contínua de probabilidades. Na verdade, existem curvas diferentes, dependendo de um parâmetro k chamado graus de liberdade aleatoriamente.

Suas propriedades são:

-A área sob a curva é igual a 1.

-Os valores de χ² Eles são positivos.

-A distribuição é assimétrica, ou seja, tem preconceitos.

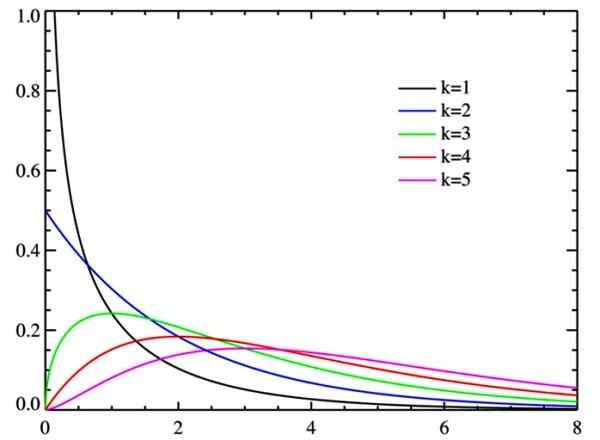Figura 2. Distribuição quadrada do chi para watts graus de liberdade. Fonte: Wikimedia Commons.

Graus de liberdade

À medida que os graus de liberdade aumentam, a distribuição do qui-quadrado tende ao normal, como pode ser visto na figura.

Para uma determinada distribuição, os graus de liberdade são determinados através do Tabela de contingência, qual é a tabela onde as frequências observadas das variáveis ​​são registradas.

Se uma tabela tiver F classifica e c colunas, o valor de k é:

K = (f - 1) ⋅ (c - 1)

Formulação de hipótese

Quando o teste do quadrado Chi é o ajuste, as seguintes hipóteses são formuladas:

-H_qualquer: variável x tem distribuição de probabilidade f (x) com parâmetros específicos e₁, e₂… , e_p

-H₁: X tem outra distribuição de probabilidade.

A distribuição de probabilidade que é assumida na hipótese nula pode ser, por exemplo, a distribuição normal bem conhecida, e os parâmetros seriam a média μ e o desvio padrão σ.

Além disso, a hipótese nula é avaliada com um certo nível de significância, ou seja, uma medida do erro que seria cometido ao rejeitá -lo sendo verdadeiro.

Em geral, esse nível é estabelecido de 1 %, 5 % ou 10 % e quanto menor o resultado do teste, mais confiável.

Pode servir você: Mumm

E se o teste de contingência do quadrado Chi for usado, que, como dissemos, serve para verificar a independência entre duas variáveis ​​x e y, as hipóteses são:

-H_qualquer: As variáveis ​​x e y são independentes.

-H₁: X e y são dependentes.

Novamente, é necessário especificar um nível de significância para conhecer a medida do erro ao tomar a decisão.

Como as estatísticas do qui-quadrado são calculadas?

As estatísticas de chi quadrado são calculadas da seguinte forma:

O símbolo ∑ significa "soma", que devemos fazer sobre a expressão fracionária indicada.

A soma é realizada da primeira classe i = 1 para a última, que é i = k.

Além do mais:

-F_qualquer É uma frequência observada (vem dos dados obtidos).

-F_e É a frequência esperada ou teórica (é necessário calculá -lo a partir dos dados).

Para aceitar ou rejeitar a hipótese nula, χ é calculado² Para dados observados e se compara a um valor chamado Quadrado crítico chi, que depende dos graus de liberdade k e o nível de significância α:

χ²_crítico =  χ²_{K, α}

Se, por exemplo, queremos executar o teste com um nível de significância de 1 %, então α = 0.01, se for com 5%, então α = 0.05 e assim por diante. P, o parâmetro de distribuição, como:

P = 1 - α

Esses valores quadrados críticos são determinados por tabelas que contêm o valor da área acumulada. Por exemplo, para k = 1, que representa 1 grau de liberdade e α = 0.05, equivalente a p = 1-.05 = 0.95, o valor de χ² É 3.841.

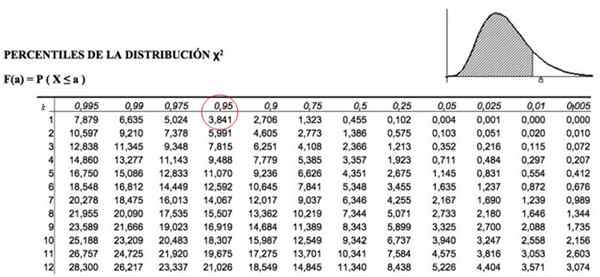Figura 3. Tabela de valores de distribuição quadrada chi. Fonte: f. Zapata.

Critérios de aceitação de CA_qualquer

Os critérios para aceitar h_qualquer é:

-Sim χ² < χ²_crítico  H_qualquer, Caso contrário, é rejeitado (veja a Figura 1).

Exemplo de cálculo

Na aplicação a seguir, o teste de chi quadrado será usado como um teste de independência.

Suponha que os pesquisadores queiram saber se a preferência pelo café preto está relacionada ao gênero da pessoa e especifique a resposta com um nível de significância de α = 0.05.

Pode atendê -lo: ângulos alternativos externos: exercícios e exercícios resolvidos

Para isso, uma amostra de 100 pessoas entrevistadas e suas respostas estão disponíveis:

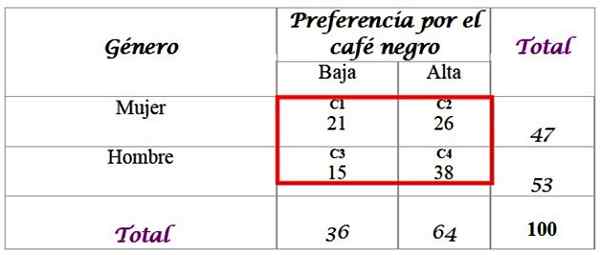
Passo 1

Estabelecer hipóteses:

-H_qualquer: Gênero e preferência pelo café preto são independentes.
-H₁: O gosto pelo café preto está relacionado ao gênero da pessoa.

Passo 2

Calcule as frequências esperadas para distribuição, para a qual são necessárias o total adicionado na última linha e na coluna de ar direita. Cada célula na caixa vermelha tem um valor esperado F_e, que é calculado multiplicando o total de sua linha R F pela coluna total C, dividida pela amostra total n:

F_e = (F x c) /n

Os resultados são os seguintes para cada célula:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

etapa 3

Então você deve calcular a estatística Chi Cuadrado para esta distribuição, de acordo com a fórmula especificada:

χ²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Passo 4

Determinar χ²_crítico, Sabendo que os dados registrados estão em f = 2 linhas e c = 2 colunas, portanto, o número de graus de liberdade é:

K = (2-1) ⋅ (2-1) = 1.

O que significa que devemos olhar na tabela mostrada acima do valor de χ²_{K, α} = χ²_{1; 0.05} , o qual é:

χ²_crítico = 3.841

Etapa 5

Compare os valores e decida:

χ² = 2.9005

χ²_crítico = 3.841

Desde χ² < χ²_crítico A hipótese nula é aceita e conclui -se que a preferência pelo café preto não está ligada ao gênero da pessoa, com um nível de significância de 5%.

Referências

1. Teste quadrado de chi para independência. Recuperado de: SaylordOtorg.Github.Io.
2. Onda médica. Estatísticas aplicadas às ciências da saúde: o teste ji-quadrado. Recuperado de: medwave.Cl.
3. Probabilidades e estatísticas. Teste de bondade de ajuste quadrado xi. Recuperado de: Probabilidades Andestics.com.
4. TRIOLA, m. 2012. Estatísticas elementares. 11º. Edição. Addison Wesley.
5. Unam. Teste quadrado de chi. Recuperado de: Advisory.Cuautitlan2.Unam.mx.