Teste de Mann - Whitney O que é e quando se aplica, execução, exemplo

O Teste de Mann - Whitney É aplicado para comparar duas amostras independentes quando elas têm poucos dados ou não seguem uma distribuição normal. Dessa forma, é considerado um teste não paramétrico, Ao contrário do seu colega Teste T do aluno, que é usado quando a amostra é grande o suficiente e segue a distribuição normal.

Frank Wilcoxon propõe -o pela primeira vez em 1945, para amostras de tamanhos idênticos, mas dois anos depois foi estendido no caso de amostras de tamanho diferente por Henry Mann e D. R. Whitney.

figura 1. O teste U de Mann - Whitney é aplicado para a comparação de amostras independentes. Fonte: Pixabay.

Freqüentemente o teste é aplicado para verificar se há uma relação entre uma variável qualitativa e outro quantitativo.

Um exemplo ilustrativo é levar um conjunto de pessoas hipertensas e extrair dois grupos, para quem os dados diários da pressão arterial são registrados por um mês.

Para um grupo, o tratamento a e outro é aplicado o tratamento b. Aqui a pressão arterial é a variável quantitativa e o tipo de tratamento é o qualitativo.

Você quer saber se a mediana, e não a média, dos valores medidos é estatisticamente igual ou diferente, para estabelecer se há uma diferença entre os dois tratamentos. Para obter a resposta, o Wilcoxon ou U -Test of Mann - Whitney é aplicado.

[TOC]

Abordagem de problema no teste U de Mann - Whitney

Outro exemplo em que o teste pode ser aplicado é o seguinte:

Suponha que você queira saber se o consumo de refrigerantes difere significativamente em duas regiões do país.

Um deles é chamado Região A e a outra região B. É realizado um registro dos litros consumidos semanalmente em duas amostras: uma das 10 pessoas para a região A e outra de 5 pessoas para a região B.

Os dados são os seguintes:

-Região a: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Região b: 12,14, 11, 30, 10

A seguinte pergunta é levantada:

O consumo de refrigerantes (y) depende da região (x)?

Variáveis ​​qualitativas versus variáveis ​​quantitativas

-Variável qualitativa x: Região

-Variável quantitativa e: Consumo gasoso

Se a quantidade de litros consumidos é a mesma nas duas regiões, a conclusão será que não há dependência entre as duas variáveis. A maneira de saber é comparar a tendência média ou mediana para as duas regiões.

Caso normal

Se os dados seguiram uma distribuição normal, duas hipóteses serão levantadas: o H0 nulo e a alternativa H1 através da comparação entre os meios:

Pode atendê -lo: produtos notáveis

-H0: Não há diferença entre a média das duas regiões.

-H1: Os meios de ambas as regiões são diferentes.

Caso sem - tendência normal

Pelo contrário, se os dados não seguirem uma distribuição normal ou simplesmente a amostra é muito pequena para saber, em vez de comparar a média, seria comparado A mediana Das duas regiões.

-H0: Não há diferença entre a mediana das duas regiões.

-H1: Os medianos de ambas as regiões são diferentes.

Se as medianas coincidem, a hipótese nula é cumprida: não há relação entre o consumo de refrigerante e a região.

E se o contrário acontecer, a hipótese alternativa é verdadeira: existe uma relação entre consumo e região.

É para esses casos em que o teste U de Mann - Whitney é indicado.

Amostras de amostra ou não com pares

A questão importante a seguir para decidir se o teste U de Mann Whitney é aplicado, é se o número de dados em ambas as amostras é idêntico, o que é equivalente a dizer que eles são ao mesmo tempo.

Se as duas amostras estiverem emparelhadas, a versão Wilcoxon original se aplicaria. Mas se não, como é o caso do exemplo, o teste Wilcoxon modificado é aplicado, que é precisamente o teste U de Mann Whitney.

Mann Whitney U Teste das características

O teste U de Mann -Whitney é um teste não paramétrico, aplicável a amostras que não seguem a distribuição normal ou com poucos dados. Tem as seguintes características:

1.- Compare os medianos

2.- Trabalhos em intervalos ordenados

3.- É menos poderoso, compreensão pelo poder, a probabilidade de rejeitar a hipótese nula quando, na realidade, é falsa.

Levando em consideração essas características, o teste U de Mann - Whitney é aplicado quando:

-Os dados são independentes

-Eles não seguem a distribuição normal

-A hipótese nula H0 é aceita se o meio das duas amostras coincidir: ma = mb

-A hipótese alternativa H1 é aceita se o meio das duas amostras diferentes: ma ≠ mb

Fórmula de Mann - Whitney

A variável u é a estatinidade de contraste usada no teste de Mann - Whitney e é definida:

U = min (ua, ub)

Isso significa que u é o menor dos valores entre UA e UB, aplicado a cada grupo. Em nosso exemplo, seria para cada região: a o b.

As variáveis ​​UA e UB são definidas e calculadas de acordo com a seguinte fórmula:

Ua = nb + na (na +1)/2 - ra

Ub = nb + nb (nb +1)/2 - rb

Pode atendê -lo: redução de termos semelhantes

Aqui os valores de NA e NB são os tamanhos das amostras correspondentes às regiões A e B, respectivamente e, por outro somas de alcance que vamos definir abaixo.

Etapas para aplicar o teste

1.- Encomende os valores das duas amostras.

2.- Atribuir um intervalo de pedidos a cada valor.

3.- Corrija as ligantes existentes nos dados (valores repetidos).

4.- Calcule RA = soma dos intervalos da amostra a.

5.- Encontre rb = soma dos intervalos da amostra B.

6.- Determine o valor UA e UB, de acordo com as fórmulas fornecidas na seção anterior.

7.- Compare UA e UB, e o menor dos dois é atribuído à estatística experimental (ou seja, os dados) em comparação com a estatística teórica ou normal.

Aplicação prática de aplicação

Agora aplicamos o acima mencionado ao problema do refrigerante anteriormente elevado:

Região A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Região B: 12,14, 11, 30, 10

Dependendo de que os meios de ambas as amostras sejam estatisticamente iguais ou diferentes, passamos a aceitar ou rejeitar a hipótese nula: não há relação entre a variável e e x, ou seja, o consumo de refrigerante não depende da região:

H0: MA = MB

H1: ma ≠ mb

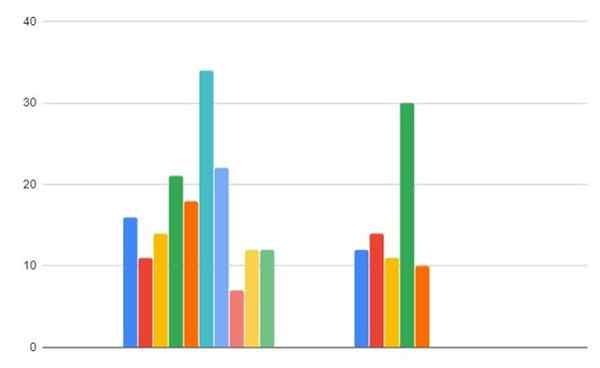Figura 2. Dados de consumo gasoso nas regiões A e B. Fonte: f. Zapata.

- Passo 1

Passamos a ordenar os dados em conjunto para as duas amostras, ordenando os valores do menos para o maior:

Observe que o valor 11 aparece 2 vezes (uma vez em cada amostra). Originalmente, possui posições ou faixas 3 e 4, mas não para superestimar ou subestimar uma ou outra, o valor médio é escolhido como um intervalo, ou seja, 3,5.

Da mesma forma, o valor 12 é prosseguido, que é repetido três vezes com as faixas 5, 6 e 7.

Bem, o valor 12 recebe o intervalo médio de 6 = (5+6+7)/3. E o mesmo para o valor 14, que tem ligação (aparece em ambas as amostras) nas posições 8 e 9, o intervalo médio 8 é atribuído.5 = (8+9)/2.

- Passo 2

Os dados da região A e B são então separados novamente, mas agora seus intervalos correspondentes são atribuídos em outra linha:

Região a

Região b

As faixas de RB são obtidas das somas dos elementos da segunda linha para cada caso ou região.

etapa 3

Os respectivos valores de UA e UB são calculados:

UA = 10 × 5 + 10 (10 + 1)/2 - 86 = 19

UB = 10 × 5 + 5 (5 + 1)/2 -34 = 31

Valor experimental u = min (19, 31) = 19

Passo 4

O teórico deve seguir uma distribuição normal n com parâmetros dados exclusivamente pelo tamanho das amostras:

Pode atendê -lo: números irracionais: história, propriedades, classificação, exemplos

N ((Na⋅nb) /2, √ [nb (na + nb +1) /12])

Para comparar a variável ou obtida experimentalmente, com a teórica, é necessário fazer uma mudança variável. Vai da variável ou experimental ao seu valor tipificado, que será chamado Z, Para poder comparar com o de uma distribuição normal tipificada.

A mudança variável é a seguinte:

Z = (u - na.NB / 2) / √ [Na. NB (Na + NB + 1) / 12] 

Deve -se notar que, para a mudança de variável, os parâmetros da distribuição teórica para u foram usados. Em seguida, a nova variável Z, que é um híbrido entre o teórico e o experimental ou uma distribuição normal tipificada n (0,1).

Critérios de comparação

Se z ≤ zα ⇒ A hipótese nula H0 é aceita

Sim z> zα ⇒ A hipótese nula H0 é rejeitada

Os valores críticos que Zα tipificou depende do nível de confiança necessário, por exemplo, para um nível de confiança α = 0,95 = 95%, o mais usual tem o valor crítico zα = 1,96.

Para os dados mostrados aqui:

Z = (u - nb / 2) / √ [nb (na + nb + 1) / 12] = -0,73

Que está abaixo do valor crítico 1,96.

Então a conclusão final é que a hipótese nula é aceita:

Não há diferença no consumo de refrigerante entre as regiões A e B.

Calculadoras on -line para o teste U de Mann - Whitney

Existem programas específicos para cálculos estatísticos, incluindo SPSS e Minitab, mas esses programas são pagos e seu uso nem sempre é simples. Isso ocorre porque eles dão tantas opções, que seu uso é praticamente reservado para especialistas em estatística.

Felizmente, existem vários programas on -line muito precisos, gratuitos e simples -que permitem, entre outros, testes u -whitney u.

Esses programas são:

-Estatísticas de Ciências Sociais (Socscistatistics.com), que tem o teste U-Whitney U e Wilcoxon no caso de amostras equilibradas ou emparelhadas.

-Estatística de terapia de IA (AI-terapia.com), que possui vários dos testes de estatística descritiva usuais.

-Estatística de usar (física.CSBSJU.Edu.

Referências

1. Dietrichson. Métodos quantitativos: teste de intervalos. Recuperado de: bookdown.org
2. Marín J p. Guia do SPSS: Análise e procedimentos em testes não paramétricos. Recuperado de: halweb.Uc3m.é
3. MOOC USAL. Teste não paramétrico: U of Mann - Whitney. Recuperado de: youtube.com
4. Wikipedia. Teste de Mann - Whitney. Recuperado de: é.Wikipedia.com
5. Xlstat. Centro de ajuda. Tutorial de teste de Mann - Whitney no Excel. Recuperado de: ajuda.Xlsat.com