Coordenadas retangulares Exemplos e exercícios resolvidos

As Coordenadas retangulares o cartesiano são aqueles que são obtidos quando projetados ortogonalmente nos três eixos cartesianos x, y, z um ponto localizado no espaço tridimensional.

Os eixos cartesianos são mutuamente orientados perpendiculares retos. No sistema de coordenadas cartesianas, três números reais que são suas coordenadas retangulares são atribuídas a cada ponto no espaço.

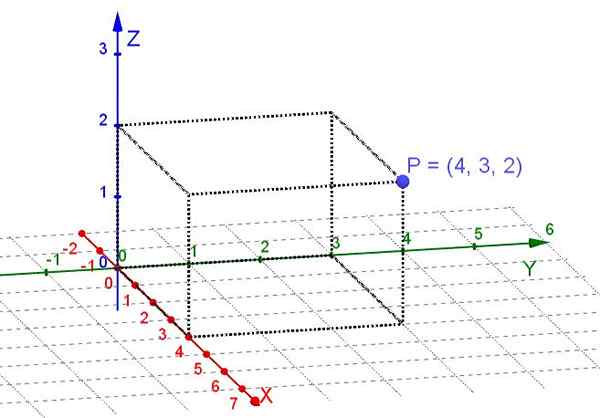
figura 1. Coordenadas retangulares do ponto P (elaboração própria)

Um avião é um subespaço do espaço tridimensional. No caso de considerar pontos em um avião, basta escolher um par de eixos perpendiculares x e como um sistema cartesiano. Então, em cada ponto do avião, dois números reais são atribuídos a ele que suas coordenadas retangulares são.

[TOC]

Origem de coordenadas retangulares

As coordenadas retangulares foram originalmente propostas pelo matemático francês René Descartes (1596 e 1650), e é por isso que eles recebem a denominação de cartesianos.

Com essa idéia de Descartes, os pontos do avião e do espaço recebem números, para que os números geométricos tenham associado uma equação algébrica e os teoremas geométricos clássicos podem ser demonstrados algebraicamente. Com coordenadas cartesianas, a geometria analítica nasceu.

O avião cartesiano

Se em um plano, duas linhas perpendiculares são escolhidas que se cruzam em um ponto ou; E se também cada linha recebe uma direção e uma escala numérica entre pontos equidistantes sucessivos, existe um sistema ou plano cartesiano no qual cada ponto do plano está associado a um par ordenado de dois números reais que são suas projeções, respectivamente, no X e Y eixos.

Pontos a = (3, 2); B = (-2, 3); C = (-2, -3) e d = (3, -3) são representados no plano cartesiano, como mostrado abaixo:

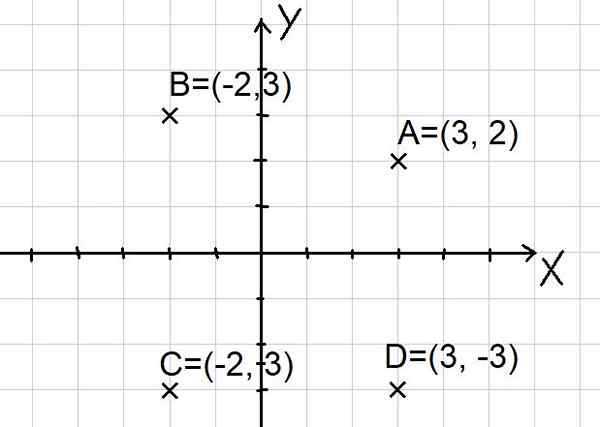Figura 2. Pontos no avião cartesiano. (Elaboração própria)

Observe que os dois eixos X e Y dividem o plano em quatro setores chamados quadrantes. O ponto A está no primeiro quadrante, o B no segundo quadrante, o C no terceiro quadrante e o ponto D no quarto quadrante.

Pode atendê -lo: população e amostra

Distância entre dois pontos

A distância entre dois pontos A e B do plano cartesiano é o comprimento do segmento que os une. Essa distância pode ser calculada analiticamente da seguinte maneira:

D (a, b) = √ (bx - ax)^2 + (por - ay)^2)

A fórmula anterior é obtida aplicando o teorema de Pitágoras.

A aplicação da referida fórmula aos pontos A, B da Figura 2 é:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

Isto é, que d (a, b) = 5,10 unidades. Observe que a distância foi obtida sem a necessidade de medir com uma regra, um procedimento completamente algébrico foi seguido.

Expressão analítica de uma linha

Coordenadas retangulares permitem a representação analítica de objetos geométricos fundamentais, como o ponto e a linha. Dois pontos A e B definem uma única linha. A inclinação da linha é definida como o quociente entre a diferença nas coordenadas e o ponto B menos, dividido pela diferença nas coordenadas x do ponto B menos a: a:

pendente = (por - ay)/(bx - ax)

Um ponto de coordenadas de qualquer ponto (x, y) que pertence à linha (AB) deve ter a mesma inclinação:

pendente = (y - ay)/(x - ax)

A equação obtida pela igualdade das inclinações é a representação analítica ou algébrica da linha que passa pelos pontos A e B:

(y - ay)/(x - ax) = (por - ay)/(bx - ax).

Se você for levado para A e B, as coordenadas retangulares da Figura 2 são:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

Nesse caso em particular, há uma linha com uma inclinação negativa -⅕, o que significa que localizado em um ponto da linha e aumentando a coordenada X em uma unidade, a coordenada e diminui em 0,2 unidades. 

Pode atendê -lo: toroid ou Toro dona

A maneira mais comum de escrever a equação da linha no avião é com a coordenada e clara em função da variável x:

y = -(1/5) x + 13/5 

Exemplos

Exemplo 1

Obtenha por métodos analíticos a distância entre os pontos c e a, sendo as coordenadas retangulares de c = (-2, -3) e as de A = (3.2).

A fórmula da distância euclidiana entre esses dois pontos é escrita assim:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Substituindo suas coordenadas retangulares correspondentes que você possui:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7,07

Exemplo 2

Obtenha a equação da linha que passa pelo ponto C das coordenadas (-2, -3) e o ponto P de coordenadas (2, 0).

Primeiro, a inclinação da linha CP é obtida:

pendente = (0 -(-3)) / (2 -( -2)) = ¾ 

Um ponto Q de coordenadas retangulares genéricas (x, y) que pertence à linha CP deve ter a mesma inclinação:

pendente = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

Ou seja, a equação da linha CP é:

(Y +3) / (x +2) = ¾

Uma maneira alternativa de escrever a equação da linha CP é limpar e:

y = ¾ x - 3/2 

Exercícios resolvidos

Exercício 1

Obtenha as coordenadas retangulares do ponto de interseção entre as linhas y = - (1/5) x + 13/5 e a linha y = ¾ x - 3/2.

Solução: Por definição, o ponto de interseção das duas linhas compartilha as mesmas coordenadas retangulares. Portanto, as coordenadas e no ponto de interseção são idênticas para ambas as linhas:

-(1/5) x + 13/5 = ¾ x - 3/2

O que leva à seguinte expressão:

Pode servir a você: trapezóide retângulo: propriedades, relacionamentos e fórmulas, exemplos

(¾ + ⅕) x = 13/5 +3/2

É obtido resolver a soma das frações:

19/20 x = 41/10

Limpeza x:

x = 82/19 = 4,32

Para obter o valor e a interseção, o valor x obtido em uma das linhas é substituído:

y = ¾ 4,32 - 3/2 = 1,74

Isso significa que as linhas dadas são interceptadas no ponto I das coordenadas i = (4,32; 1,74).

Exercício 2

Obtenha a equação de circunferência que passa pelo ponto de coordenada retangular R (3, 4) e que tem um centro na origem das coordenadas.

Solução: Rádio R é a distância do ponto R à origem ou coordenadas (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Isto é, é um raio 5 círculo 5 centrado em (0,0).

Um ponto p (x, y) da circunferência deve ter a mesma distância 5 ao centro (0, 0) para o que pode ser escrito:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

Quer dizer:

√ (x^2 + y^2) = 5

Para eliminar a raiz quadrada, ambos os membros da igualdade são deixados em silêncio:

x^2 + y^2 = 25

Qual é a equação de circunferência.

Com este exemplo, o poder do sistema de coordenadas retangulares é ilustrado, o que permite determinar objetos geométricos, como a circunferência sem a necessidade de usar papel, lápis e bússola. A circunferência solicitada apenas por métodos algébricos foi determinada.

Referências

1. Arfken G e Weber H. (2012). Métodos matemáticos para físicos. Um guia abrangente. 7ª edição. Academic Press. ISBN 978-0-12-384654-9
2. Cálculo do CC. Coordenadas retangulares resolvidas problemas. Recuperado de: cálculo.DC
3. Weisstein, Eric W. "Coordenadas cartesianas.”De Mathworld-A Wolfram Web. Recuperado de: Mathworld.Volfrâmio.com
4. Wikipedia. Sistema de coordenada cartesiana. Recuperado de: em.Wikipedia.com