Coordenadas esféricas Exemplos e exercícios resolvidos

As Coordenadas esféricas Eles são um sistema de localização de pontos no espaço tridimensional que consiste em uma coordenada radial e duas coordenadas angulares chamadas coordenadas polares e coordenadas azimutais.

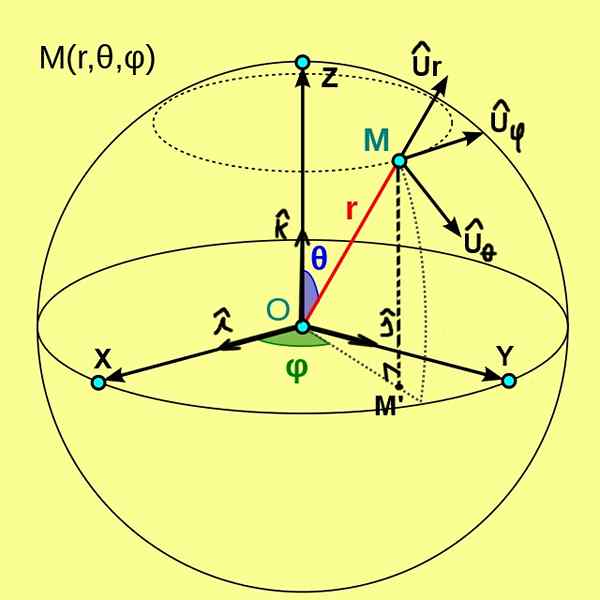
Na Figura 1, que vemos abaixo, as coordenadas esféricas (r, θ, φ) de um ponto m são mostradas. Essas coordenadas são referidas a um sistema ortogonal de eixos cartesianos x, y, z de origem ou.

figura 1. Coordenadas esféricas (r, θ, φ) de um ponto m. (Wikimedia Commons)

Nesse caso, a coordenada r do ponto m é a distância desse ponto até a origem ou. A coordenada polar θ representa o ângulo entre a semi -axis positiva z e o raio vetorial om. Enquanto a coordenada azimutal φ é o ângulo entre o eixo semi -eixo positivo e o raio vetorial om ', sendo m' a projeção ortogonal de m no plano XY.

A coordenada radial r leva apenas valores positivos, mas se um ponto estiver localizado na origem, então r = 0. A coordenada polar θ leva como um valor mínimo 0º para pontos localizados no semi -tribo positivo. Finalmente, a coordenada azimutal φ leva como valor mínimo 0º e nível máximo de 360º.

0 ≤ r < ∞

0 ≤ θ ≤ 180º

0 ≤ φ  < 360º

[TOC]

Mudança de coordenadas

Em seguida, as fórmulas que permitem que as coordenadas cartesianas (x, y, z) de um ponto M sejam dadas, assumindo o ponto de coordenadas esféricas do mesmo (r, θ, φ): ponto:

x = r sen (θ) cos (φ)

y = r sen (θ) sin (φ) 

z = r cos (θ)

Da mesma forma, é útil encontrar as relações para passar das coordenadas cartesianas (x, y, z) de um ponto dado às coordenadas esféricas desse ponto:

R = √ (x^2 + y^2 + z^2)

θ = arcan (√ (x^2 + y^2) / z)

Pode atendê -lo: variável aleatória discreta

φ = arctan (y / x)

Base vetorial em coordenadas esféricas

Das coordenadas esféricas, é definida uma base ortonormal de vetores de base, que são denotados por Ur, Uθ, Uφ. A Figura 1 mostra esses três vetores de unidade, que têm as seguintes características:

- Ur É o vetor unitário tangente à linha radial θ = ctte e φ = ctte;

- Uθ É o vetor tangente unitário ao arco φ = ctte e r = ctte;

- Uφ É o vetor unitário tangente ao arco r = ctte e θ = ctte.

Elementos de linha e volume em coordenadas esféricas

A posição vetorial de um ponto no espaço nas coordenadas esféricas é escrita assim:

r = r Ur

Mas uma variação ou deslocamento infinitesimal de um ponto no espaço tridimensional, nessas coordenadas, é expresso pelo seguinte relacionamento vetorial:

dr = dr Ur + R Dθ Uθ + r sen (θ) dφ Uφ

Finalmente, um DV de volume infinitesimal nas coordenadas esféricas é escrito assim:

dv = r^2 sin (θ) dr dθ dφ

Esses relacionamentos são muito úteis para o cálculo de integrais de linha e volume em situações físicas que têm simetria esférica.

Relacionamento com coordenadas geográficas

As coordenadas geográficas são entendidas que elas servem para localizar lugares na superfície da Terra. Este sistema usa as coordenadas de latitude e comprimento para localizar a posição na superfície da terra.

No sistema de coordenadas geográficas, a superfície da Terra é suposta.

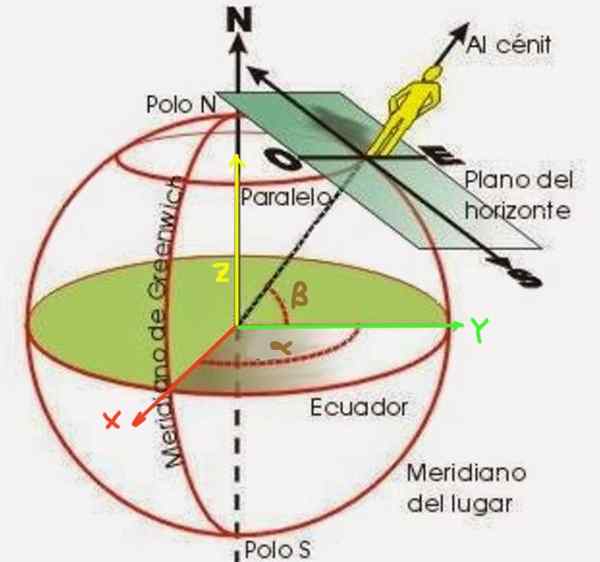Figura 2. Latitude α e β de comprimento de um observador na superfície da Terra.

A latitude β é um ângulo formado por um raio que começa do centro da terra até o ponto em que você deseja posicionar. É medido a partir do plano equatorial, como mostrado na Figura 2. Por outro lado, o comprimento α é o ângulo que o meridiano do ponto que está colocando em relação ao meridiano zero (conhecido como Greenwich meridian).

Pode atendê -lo: valor relativo

A latitude pode ser a latitude norte ou sul, dependendo se o local que está sendo localizado está no hemisfério norte ou no hemisfério sul. Da mesma forma, o comprimento pode ser oeste ou dependendo se o local é oeste ou leste do zero meridiano.

Fórmulas para mudar de geográfico para esférico

Para obter essas fórmulas, a primeira coisa é estabelecer um sistema de coordenadas. O avião XY é escolhido coincidindo com o plano equatorial, sendo o semi -eixo positivo que vai do centro da terra e através do meridiano zero. Por sua vez, o eixo e passa pelo 90º e meridiano. A superfície da Terra tem rádio RT.

Com este sistema de coordenadas, as transformações geográficas a esféricas são assim:

αEβn → (RT, θ = 90º-β, φ = α)

αOβn → (RT, θ = 90º-β, φ = 360º-α)

αEβ → (RT, θ = 90º+β, φ = α)

αOβS → (RT, θ = 90º+β, φ = 360º-α) 

Exemplos

Exemplo 1

As coordenadas geográficas de Palma de Mallorca (Espanha) são:

Comprimento leste 38.847º e latitude norte 39.570º. Para determinar as coordenadas esféricas correspondentes a Palma de Maiorca, a primeira das fórmulas das fórmulas da seção anterior é aplicada:

38.847ºEE39.570ºn → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)

Então as coordenadas esféricas são:

Palma de Maiorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)

Na resposta anterior, r igual ao raio médio da terra foi tomado.

Exemplo 2

Sabendo que as Ilhas Malvinas (Malvinas) têm coordenadas geográficas 59ºO 51,75ºs, determine as coordenadas polares correspondentes. Lembre -se de que o eixo X vai do centro da terra para o meridiano de 0º e no plano equatorial; o eixo y também no plano equatorial e através do meridiano oeste de 90º; Finalmente o eixo Z no eixo da rotação terrestre na direção sul-norte.

Pode servir a você: Curtose: Definição, Tipos, Fórmulas, para que é, por exemplo,

Para encontrar as coordenadas esféricas correspondentes, usamos as fórmulas apresentadas na seção anterior:

59ºO 51,75ºs → (r = 6371 km, θ = 90º+51,75º, φ = 360º-59º) isto é, ou seja,

Malvinas: (r = 6371 km, θ = 141,75º, φ = 301º)

Exercícios

Exercício 1

Encontre as coordenadas cartesianas de Palma de Maiorca no sistema de referência Cartesiano XYZ mostrado na Figura 2.

Solução: Anteriormente, no Exemplo 1, as coordenadas esféricas foram obtidas com base nas coordenadas geográficas de Palma de Maiorca. Para que as fórmulas apresentadas acima possam ser usadas para passar de esféricas para cartesianos:

x = 6371 km sen (50,43º) cos (38,85º)

Y = 6371 km sen (50,43º) sen (38,85º) 

Z = 6371 km cos (50,43º)

Realizar os cálculos correspondentes são:

Palma de Maiorca: (x = 3825 km, y = 3081 km, z = 4059)

Exercício 2

Encontre as coordenadas cartesianas das ilhas das Malvinas no sistema de referência Cartesiano XYZ mostrado na Figura 2.

Solução: Anteriormente, no Exemplo 2, as coordenadas esféricas foram obtidas com base nas coordenadas geográficas das Ilhas das Malvinas. Para que as fórmulas apresentadas acima possam ser usadas para passar de esféricas para cartesianos:

x = 6371 km sen (141,75º) cos (301º)

y = 6371 km sen (141,75º) sen (301º) 

Z = 6371 km cos (141,75º)

É obtido realizar os cálculos correspondentes:

Ilhas Falkland: (x = 2031 km, y = -3381 km, z = -5003)

Referências

1. Arfken G e Weber H. (2012). Métodos matemáticos para físicos. Um guia abrangente. 7ª edição. Academic Press. ISBN 978-0-12-384654-9
2. Cálculo do CC. Coordenadas cilíndricas e esféricas resolvidas. Recuperado de: cálculo.DC
3. Oficina de astronomia. Latitude e longitude. Recuperado de: Taxa.Blogspot.coma
4. Weisstein, Eric W. “Coordenadas esféricas.”De Mathworld-A Wolfram Web. Recuperado de: Mathworld.Volfrâmio.com
5. Wikipedia. Sistema de coordenadas esféricas. Recuperado de: em.Wikipedia.com
6. Wikipedia. Campos vetoriais em coordenadas cilíndricas e esféricas. Recuperado de: em.Wikipedia.com