Conservação do Princípio, Exemplos, Exemplos, Exercícios Lineares.

O Conservação do momento linear de um corpo estabelece que o produto de sua massa por seu vetor de velocidade é uma quantidade constante, quando o corpo está livre de interação com outros corpos e com a velocidade medida em relação a um sistema de referência fixo ou não agudo.

Quando existem vários corpos que interagem apenas entre eles, mas não com o ambiente externo, então o momento linear do conjunto também permanece constante ao longo do tempo.

Um astronauta no espaço está livre de toda a interação, portanto, seu momento linear

O momento linear, quantidade de movimento linear ou simplesmente o momento, É indicado com a carta p E é uma quantidade de vetor:

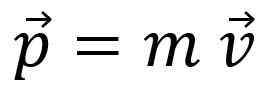
O momento linear não é o mesmo que a velocidade, embora a proporção seja evidente: por exemplo, um caminhão que vai para 20 km/h tem mais tempo linear do que uma bicicleta que se move na mesma velocidade.

Para que o momento linear de um corpo mude, é necessário que uma força externa líquida esteja agindo sobre ele, caso contrário, permanece constante. Além disso, o momento linear P de um sistema formado por N-corpo É a soma vetorial de momentos individuais:

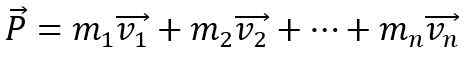
[TOC]

Princípio da conservação da quantidade de movimento linear

Em um corpo livre de forças (ou uma em que todas as forças nele são canceladas), acontece que o momento linear.

Da mesma forma, passa em um sistema formado por vários corpos que apenas interagem entre si, mas não com o ambiente externo: o momento linear total do sistema permanece fixo durante a evolução do conjunto do conjunto.

Este princípio de conservação é declarado assim:

O momento linear total de um conjunto de N-Body que apenas interage entre si, mas não com o ambiente externo, é uma quantidade invariável no tempo.

E matematicamente, é expresso da seguinte maneira:

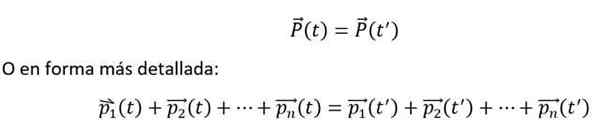
A igualdade anterior é cumprida, se e somente se o n-Os corpos interagem entre si, mas não com o ambiente externo. Além disso, momentos individuais devem sempre ser medidos em relação a um sistema de referência inercial.

Exemplos

Exemplo 1

Dois astronautas no espaço são retirados das mãos e permanecem em uma posição fixa em relação ao navio. Mas eles se empurram, começam a se separar em direções opostas, quando são vistas do navio.

Pode servir a você: Teoria do Big Bang: características, estágios, evidências, problemas

Nesse caso, como a interação entre astronautas está apenas entre eles através da força de contato de suas mãos, o momento linear total. Isto é, tempo linear total 0.

No entanto, o momento linear de cada astronauta mudou. Inicialmente, cada um teve um momento linear 0 em relação ao navio, mas depois de empurrar um sai em uma direção e o outro na direção oposta, com momentos lineares não nulos de igual magnitude e endereços contrários.

Assim, quando os momentos individuais são adicionados vetorialmente, o momento linear total inicial é obtido como resultado, o que é anulado.

Por outro lado, a conservação da quantidade de momento linear. Mas o resultado de multiplicar sua massa por sua velocidade é igual ao produto obtido multiplicando a massa do outro pela velocidade do outro.

Exemplo 2

Um filhote está em uma plataforma flutuante em um lago de águas calmas e seu proprietário o vê de uma doca. No começo, a plataforma e o filhote estão em repouso, mas quando o filhote quer se aproximar do proprietário, a plataforma se afasta da doca.

A explicação para esta observação está precisamente no princípio da conservação da quantidade de momento linear. O sistema consiste no filhote e na plataforma.

O filhote pode andar na plataforma graças à força de atrito entre as pernas e a superfície, neste caso a força de atrito é uma força interna de interação entre ela e a plataforma.

O conjunto é um sistema isolado e a plataforma pode se mover horizontalmente no lago, livre de toda a resistência do movimento. Por outro lado, na direção vertical, todas as forças são equilíbrio e compensadas, e o conjunto não tem movimento nessa direção.

Portanto, nessa situação, todas as hipóteses são atendidas para que o princípio da conservação do momento linear seja aplicado.

Exemplo 3

Um esquimó é capturado no centro de um sorvete, o gelo é tão suave que, por mais que seja tentado, o Eskimo desliza e sempre permanece no mesmo lugar.

A única maneira possível de que o esquimó sai do lago é que ele está na direção contrária a que um objeto pesado que carrega em sua mochila (assumindo uma).

Pode atendê -lo: óptica geométrica: que estudos, leis, aplicações, exercícios

Formulários

Navio no espaço

A conservação do momento linear. Nesse caso, o impulso do navio é alcançado pela expulsão de gases em alta velocidade, para que o foguete possa se mover na direção oposta à qual foram expulsos.

Se o navio estiver originalmente em repouso, quando o combustível é queimado e expulso, a força da expulsão ocorre contra o próprio navio. É uma força interna entre os gases e o navio. Não há forças externas e, portanto, aplica a conservação do momento linear.

Como o momento linear dos gases é o mesmo e contrário ao do navio, ele consegue deixar descansar e, continuando a expulsar gases, aumenta sua quantidade de movimento e, portanto, sua velocidade.

Vida quotidiana

Outro caso para a conservação do momento linear.

Pode -se argumentar que, neste caso, o princípio não se aplica, porque há uma força externa: a resistência oferecida pela madeira ao cravo.

No entanto, no momento do contato, a força que o martelo imprime na unha é uma força interna (entre o sistema que é a unha e o martelo) muito maior que a resistência que a madeira se opõe e, portanto, a última é desprezível.

Todo o momento linear do martelo, que é bastante grande devido à sua grande massa e velocidade, é transferida para a unha logo após a colisão. Observe que todo o momento é transferido, mas não toda a energia cinética do martelo, uma vez que parte dela é transformada em energia térmica na unha e no martelo, que aumentam sua temperatura após o impacto.

Exercícios

Exercício 1

Os astronautas de Andrew e Berenice estão fora da estação espacial retirada das duas mãos e do repouso em relação à estação. Eles dirigem estão empurrando as mãos contra as do outro e são liberadas. Se Andrew, 70 kg de massa se move a 1 m/s em relação à estação, o que é a velocidade de Berenice com 49 kg de massa?

Solução

Nesse caso, a hipótese da conservação do momento linear é claramente aplicada, pois não há forças externas no espaço externo. A força com a qual suas mãos empurram os dois astronautas é uma força interna.

Pode atendê -lo: difração de ondas: conceito e exemplos

Suponha que a massa de Andrew seja m_para e o de Berenice M_b. Da mesma forma, as velocidades de ambos após o impulso são V_para Para Andrew e V_b Para Berenice. Então a conservação do momento linear é aplicada da seguinte maneira:

M_para∙0 + M_b∙0 = M_para∙V_para+ M_b∙V_b

Limpando a velocidade de Berenice que você tem:

V_b = - (M_para / M_b) ∙ V_para

Colocando valores numéricos:

V_b = - (70/49) ∙ (1m / s) ou = -1,43m/s ou

Ou seja, que Berenice se move rapidamente 1,43 m/s na direção oposta de Andrew.

Exercício 2

Um filhote caminha em direção ao seu dono em cima de uma plataforma semi-certa. Fonte: f. Zapata.

Uma massa de 5 kg está em repouso em uma plataforma de 15 kg que flutua, também em repouso, em um lago parado. Se o filhote começar a andar na plataforma a uma taxa de 0,5 m/s em relação a isso. Com que rapidez o filhote e a plataforma em relação a um observador fixo para aterrar?

Solução

Será tomado como um sistema de referência inercial para o dock onde o proprietário do filhote está. Inicialmente, tanto o filhote quanto a plataforma flutuante estão em repouso em relação à doca.

Quando o filhote decide caminhar em direção ao proprietário rapidamente V ' Em relação à plataforma, a plataforma se afasta da primavera com velocidade +V. A velocidade do filhote em relação à doca é alcançada pela soma vetorial de sua velocidade em relação à plataforma, além da velocidade da plataforma e denota -a:

v = -v' + V

Como a resistência da água ao movimento da plataforma é praticamente nula devido à sua baixa velocidade, pode -se afirmar que o sistema composto de O filhote + a plataforma É um sistema isolado e o princípio de conservação do momento linear é aplicado:

0 = M ∙ V + M ∙ V

Lembrando que v = v ' + v você tem:

0 = -M ∙ V ' + M ∙ V + M ∙ V

Isto é: m ∙ v '= (m+m) ∙ v

Portanto v = [m/(m + m)] v 'y v = - (m/m) v = - [m/(m + m)] v'

A substituição de valores numéricos é:

V = [5/(5 +15)] ∙ 0,5m/s = 0,125 m/s

Esta é a velocidade com que a plataforma de primavera se afasta.

V = -(15/20) ∙ 0,5m/s = -0.375 m/s

E essa é a velocidade com que o filhote se aproxima do doca.

Referências

1. Universidade Duke. Sistemas de partículas. Recuperado de: webhome.Phy.Duque.Edu.
2. Rex, a. 2011. Fundamentos da Física. Pearson.
3. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. Pearson.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Ed. Cengage Learning.
5. Tipler, p. (2006). Física para Ciência e Tecnologia. 5ª ed. Volume 1. Editorial revertido.