Propriedades do conjunto finito, exemplos, exercícios resolvidos

É entendido por Conjunto finito tudo definido com um número limitado ou contábil de elementos. Exemplos de conjuntos finitos são os mármores que estão contidos em uma bolsa, o conjunto de casas em um bairro ou o conjunto P formado pelos vinte (20) números naturais:

P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 

O conjunto de estrelas do Universo é certamente imenso, mas não é conhecido com certeza se é finito ou infinito. No entanto, o conjunto de planetas do sistema solar é finito.

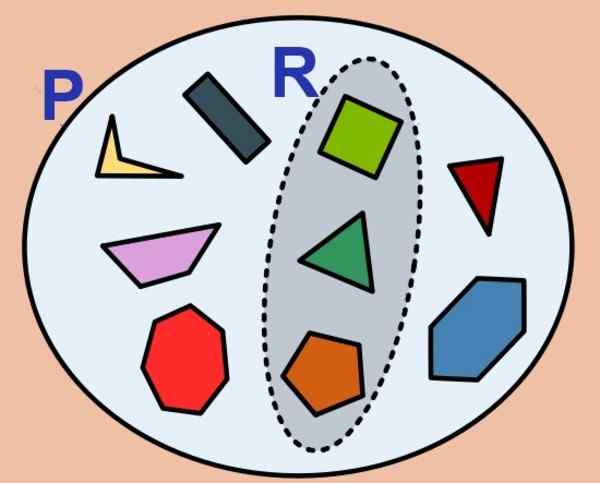
figura 1. O conjunto de polígonos é finito e o subconjunto dos regulares também. (Wikimedia Commons)

O número de elementos de um conjunto finito é chamado de cardinalidade e para o conjunto P É indicado assim: cartão (P) qualquer #P. O conjunto vazio não tem cardinalidade e é considerado um conjunto finito.

[TOC]

Propriedades

Entre as propriedades dos conjuntos finitos estão os seguintes:

1- A união de conjuntos finitos resulta em um novo conjunto finito.

2- Se dois conjuntos finitos interceptaram, é um novo conjunto finito.

3- Um subconjunto de um conjunto finito é finito e sua cardinalidade é menor ou igual à do conjunto original.

4- O conjunto vazio é um conjunto finito.

Exemplos

Existem muitos exemplos de conjuntos finitos. Entre alguns exemplos estão os seguintes:

O conjunto M Dos meses do ano, que podem ser estendidos da seguinte forma:

M = Janeiro, fevereiro, março, abril, maio, junho, julho, agosto, setembro, outubro, novembro, dezembro, a cardinalidade de M é 12.

O conjunto S dos dias da semana: S = Segunda, terça, quarta, quinta, sexta, sábado, domingo. A cardinalidade de S é 7.

Pode atendê -lo: relações de proporcionalidade: conceito, exemplos e exercícios

O conjunto Ñ Das cartas do alfabeto espanhol, é um conjunto finito, este conjunto por extensão é escrito assim:

Ñ = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z e seu A cardinalidade é 27.

O conjunto V Das vogais em espanhol, é um subconjunto do conjunto ñ:

V ⊂ Ñ Portanto, é um conjunto finito.

O conjunto finito V A maneira estendida é escrita assim: V = a, e, i, o, u e sua cardinalidade é 5.

Conjuntos podem ser expressos pela compreensão. O conjunto F Composto pelas cartas da palavra "finito" é um exemplo:

F = x / x é uma letra da palavra "finita"

Este conjunto expresso será extensivamente:

F = f, i, n, t, o cuja cardinalidade é 5 e, portanto, é um conjunto finito.

Mais exemplos

As cores do arco -íris são outro exemplo finito, o conjunto C Destas cores é:

C = vermelho, laranja, amarelo, verde, ciano, azul, violeta e sua cardinalidade é 7.

O conjunto de fases F Da Lua é outro exemplo de conjunto finito:

F = Lua nova, sala de cultivo, lua cheia, sala em declínio Este conjunto tem cardinalidade 4.

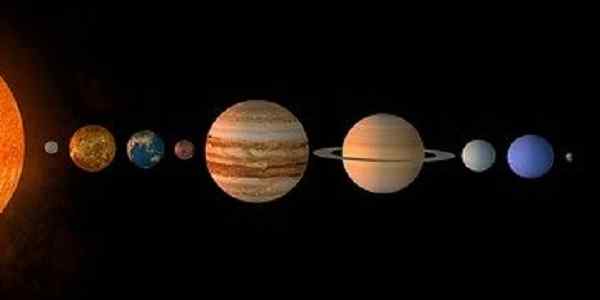Figura 2. Os planetas do sistema solar formam um conjunto finito. (Pixabay)

Outro conjunto finito é o formado pelos planetas do sistema solar:

P = Mercury, Vênus, Terra, Marte, Júpiter, Saturno, Urano, Netuno, Plutão Cardinalidade 9.

Exercícios resolvidos

Exercício 1

O seguinte conjunto é dado a = x∊ r / x^3 = 27. Expresse -o em palavras e escreva por extensão, indique sua cardinalidade e diga se é ou não finito.

Pode atendê -lo: elipse

Solução: O conjunto A é o conjunto de números reais x tal que X aumentou para o cubo como resultado 27.

Equação X^3 = 27 tem três soluções: que são x1 = 3, x2 = (-3/2 + 3√3/2 i) e x3 = (-3/2-3√3/2 i). Das três soluções apenas X1 é real, enquanto os outros dois são números complexos.

Como a definição de conjunto A diz que X pertence a números reais, as soluções em números complexos não fazem parte do conjunto para.

O conjunto estendido é:

A = 3, que é um conjunto finito de cardinalidade 1.

Exercício 2

Escreva simbolicamente (pelo entendimento) e extensivamente o conjunto B dos números reais maiores que 0 (zero) e menor ou igual que 0 (zero). Indique sua cardinalidade e se é finito ou não.

Solução: B = x∊ r / 0 < x <= 0

O conjunto B está vazio porque um número real x não pode ser simultaneamente maior e menor que zero, bem como 0 e também menor que 0.

B = e sua cardinalidade é 0. O conjunto vazio é um conjunto finito.

Exercício 3

O conjunto S das soluções de uma determinada equação é dada. O conjunto pelo entendimento é escrito assim:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Escreva este conjunto extensivamente, indique sua cardinalidade e indique se é ou não um conjunto finito.

Solução: Primeiro, analisando a expressão que descreve os conjuntos S, obtém -se que é um conjunto de valores de X reais que são soluções da equação:

(x -3) (x^2 - 9x + 20) = 0 (*)

Uma solução desta equação é x = 3, que é um número real e, portanto, pertence a s. Mas existem mais soluções que podem ser obtidas procurando as soluções da equação quadrática:

Pode atendê -lo: distribuição F: Características e exercícios resolvidos

(x^2 - 9x + 20) = 0

A expressão anterior pode levar em consideração o seguinte:

(x - 4) (x - 5) = 0

O que nos leva a mais duas soluções da equação original (*) que são x = 4 e x = 5. Em suma, a equação (*) possui soluções 3, 4 e 5.

O conjunto S expresso extensivamente é assim:

S = 3, 4, 5, que tem cardinalidade 3 e, portanto, é um conjunto finito.

Exercício 4

Existem dois conjuntos a = 1, 5, 7, 9, 11 e b = x ∊ n / x é par ^ x x x < 10 .

Escreva explicitamente Conjunto B e encontre a União com o conjunto A. Encontre também a interceptação desses dois conjuntos e conclua.

Solução: O conjunto B é composto de números naturais de modo que eles são uniformes e também sejam inferiores ao valor 10, portanto, juntos B é extensivamente escrito da seguinte forma:

B = 2, 4, 6, 8

A união do conjunto A com o conjunto B é:

A u b = 1, 2, 4, 5, 6, 7, 8, 9, 11

E a interceptação de Set A com o conjunto B é escrita assim:

A ⋂ b = = Ø é o conjunto vazio. 

Deve -se notar que a união e a interceptação desses dois conjuntos finitos levam a novos conjuntos, que por sua vez também são finitos.

Referências

1. Fontes, a. (2016). MATEMÁTICA BÁSICA. Uma introdução ao cálculo. Lulu.com.
2. Garo, m. (2014). Matemática: Equações quadráticas: Como resolver uma equação quadrática. Marilù Garo.
3. Haeussler, e. F., E Paul, r. S. (2003). Matemática para Administração e Economia. Pearson Education.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matemática 1 de setembro. Limite.
5. Precioso, c. T. (2005). Curso de Matemática 3O. Editorial Progreso.
6. Matemática 10 (2018). "Exemplos de conjuntos finitos". Recuperado de: Mathematics10.líquido
7. Rock, n. M. (2006). Álgebra eu é fácil! Tão fácil. Team Rock Press.
8. Sullivan, J. (2006). Álgebra e trigonometria. Pearson Education.
9. Wikipedia. Conjunto finito. Recuperado de: é.Wikipedia.com