Propriedades, exemplos e exercícios de base Ortonormal

A Base Ortonormal É formado com vetores perpendiculares entre si e cujo módulo também vale 1 (vetores unitários). Lembre -se disso uma base B em um espaço vetorial V, É definido como um conjunto de vetores linearmente independentes capazes de gerar este espaço.

Por sua vez, um espaço vetorial é uma entidade matemática abstrata entre cujos elementos são vetores, geralmente associados a magnitudes físicas, como velocidade, força e deslocamento ou também a matrizes, polinômios e funções.

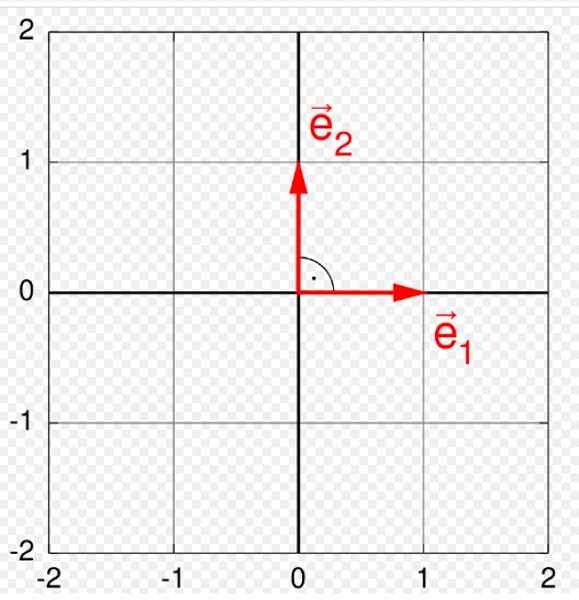
figura 1. Base ortonormal no avião. Fonte: Wikimedia Commons. Quartl [CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0)].

Os vetores têm três elementos distintos: magnitude ou módulo, direção e significado. Uma base Ortonormal é especialmente útil para representar e operar com eles, porque qualquer vetor que pertence a um determinado espaço vetorial V, Pode ser escrito como uma combinação linear dos vetores que formam a base Ortonormal.

Dessa forma, operações entre vetores, como soma, subtração e os diferentes tipos de produtos definidos no referido espaço, são analisados ​​analiticamente.

Entre as bases mais usadas da física está a base formada por vetores unitários Yo, J e k representando as três direções distintas do espaço tridimensional: alto, largo e profundidade. Esses vetores também são conhecidos pelo nome de Vetores canônicos unitários.

Se, em vez disso, os vetores forem trabalhados em um avião, seria suficiente com dois desses três componentes, enquanto apenas um.

[TOC]

Bases propriedades

1- uma base B É o menor conjunto possível de vetores que geram o espaço vetorial V.

2- Os elementos de B Eles são linearmente independentes.

3- Qualquer base B de um espaço vetorial V, permite expressar todos os vetores de V Como uma combinação linear e este formulário é único para cada vetor. Portanto a B Também é conhecido como Sistema gerador.

4- O mesmo espaço vetorial V pode ter bases diferentes.

Pode servir a você: Força Centrifugal: Fórmulas, como é calculado, exemplos, exercícios

Exemplos de bases

Abaixo de vários exemplos de bases e bases ortonormais em geral:

A base canônica em ℜ ⁿ

Também chamado de base natural ou base padrão de ℜ ⁿ, Onde ℜ ⁿ É espaço n-dimensional, Por exemplo, o espaço tridimensional é ℜ ³. Para o valor de n É chamado dimensão do espaço vetorial e denota como Dim (v).

Todos os vetores que pertencem a ℜ ⁿ Eles são representados por N-USA Ordenado. Para espaço ℜⁿ, A base canônica é:

e₁ =; e₂ =; e_n =

Neste exemplo, usamos a notação com colchetes ou "suportes" e ousados ​​para vetores de unidade e₁, e₂, e₃..

A base canônica em ℜ³

Vetores familiares Yo, J e k Eles admitem a mesma representação e são suficientes para três para representar os vetores em ℜ ³:

Yo =; J =;  k =

Isso significa que a base pode ser expressa da seguinte maneira:

B = ; ;

Para verificar se eles são linearmente independentes, o determinante formado com eles os vetores não é call e também igual a 1:

Também deve ser possível escrever qualquer vetor que pertence a ℜ ³ Como uma combinação linear deles. Por exemplo, uma força cujos componentes retangulares são f_x = 4 n, f_e = -7 n e f_z= 0 n seria escrito de forma vetorial da seguinte forma:

F = N = 4Yo -7J + 0k N.

Portanto Yo, J e k compõem um sistema de gerador ℜ ³.

Outras bases ortonormais em ℜ³

A base padrão descrita na seção anterior não é a única base ortonormal em ℜ³. Aqui temos, por exemplo, as bases:

B₁ = ; ;

B₂ = ; ;

Pode -se demonstrar que essas bases são ortonormais, pois isso lembramos das condições que devem ser atendidas:

Pode atendê -lo: Óptica ondulada

-Vetores que formam a base devem ser ortogonais um ao outro.

-Cada um deles deve ser unitário.

Podemos verificá -lo sabendo que o determinante formado por eles deve ser não -nulo e igual a 1.

Base b₁ É precisamente o das coordenadas cilíndricas ρ, φ e z, outra maneira de expressar vetores no espaço.

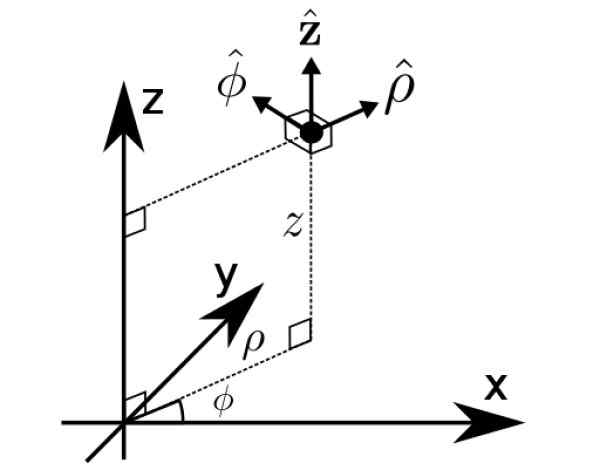Figura 2. Coordenadas cilíndricas. Fonte: Wikimedia Commons. Fustelo de matemática [CC BY-S (https: // CreativECommons.Org/licenças/BY-SA/4.0)].

Exercícios resolvidos

- Exercício 1

Mostre que a base b = ; ; é ortonormal.

Solução

Para mostrar que os vetores são perpendiculares um ao outro, usaremos o produto escalar, também chamado de ponto interno ou de produto de dois vetores.

Deixe dois vetores ou e v, Seu produto escalar é definido por:

ou • v = ou.v. cosθ

Para distinguir os vetores de seus módulos, usaremos em negrito para as primeiras e normais letras para o último. θ é o ângulo entre ou e v, Portanto, se forem perpendiculares, significa que θ = 90º e o produto escalar é nulo.

Como alternativa, se os vetores forem dados em termos de seus componentes: ou = x, ou_e,ou_z > e v = x, v_e,v_z >, o produto escalar de ambos, que é comutativo, é calculado dessa maneira:

ou • v = ou_x .v_x + ou_e .v_e + ou_z .v_z

Dessa forma, os produtos escalares entre cada par de vetores são, respectivamente:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Para a segunda condição, o módulo de cada vetor é calculado, que é obtido por:

│u │ = √ (u_x² + ou_e² + ou_z²)

Assim, os módulos de cada vetor são:

│ = √ [(3/5)² + (4/5)²  + 0²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Pode servir a você: Segundo Equilíbrio Condição: Explicação, Exemplos, Exercícios

│ = √ [0² + 0²  + 1²)] = 1

Portanto, os três são vetores de unidade. Finalmente, o determinante que eles formam não é nulo e igual a 1:

- Exercício 2

Escreva as coordenadas do vetor C = Em termos da base anterior.

Solução

Para fazer isso, o teorema a seguir é usado:

Seja B = v₁, v₂, v₃,.. v_n Uma base ortonormal no espaço V com produto doméstico, o vetor C É representado por B da seguinte maneira:

C = <C•v₁> v₁ + <C•v₂> v₂ +<C•v₃> v₃ +.. <C•v_n> v_n

Isso significa que podemos escrever o vetor na Base B, através de coeficientes <C•v₁>, <C•v₂>, ..  <C•v_n>, para o qual você deve calcular os escalares indicados:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

Com os produtos escalares obtidos, uma matriz é construída, chamada Coordenar a matriz de w.

Portanto, o vetor coordena C Na base B, eles são expressos através de:

[[C]_B= [[(18/5); (1/5); 1]

A matriz de coordenadas não é o vetor, pois um vetor não é o mesmo que suas coordenadas. Estes são apenas um conjunto de números que servem para expressar o vetor em uma determinada base, não o vetor como tal. Eles também dependem da base selecionada.

Finalmente, seguindo o teorema, o vetor C seria expresso o seguinte:

W = (18/5) v₁ + (1/5) v₂ + v₃

Com: v₁ =; v₂ =; v₃ =, Isto é, os vetores base B.

Referências

1. Larson, r. Fundamentos da álgebra linear. 6º. Edição. Cengage Learning.
2. Larson, r. 2006. Cálculo. 7º. Edição. Volume 2. McGraw Hill.
3. Salas, J. álgebra Linear. Tópico 10. Bases Ortonormais. Recuperado de: OCW.Uc3m.é.
4. Universidade Sevilla. Coordenadas cilíndricas. Base de vetores. Recuperado de: Laplace.nós.é.
5. Wikipedia. Base Ortonormal. Recuperado de: é.Wikipedia.org.