Fórmulas e equações de antiderivativas, exemplos, exercícios

A Antiderivativo F (x) de uma função F(x) também é chamado de primitivo ou simplesmente a integral indefinida da referida função, se em um determinado intervalo Yo, É verdade que F '(x) = f (x)

Por exemplo, vamos tirar a seguinte função:

f (x) = 4x³

Uma antiderivada desta função é f (x) = x⁴, Desde que derivando f (x) pela regra de derivação para os poderes:

É obtido com precisão f (x) = 4x³.

No entanto, este é apenas um dos muitos antiderivativos de f (x), pois esta outra função: g (x) = x⁴ + 2 É também, porque, derivando g (x) em relação a x, é o mesmo é obtido para trás f (x).

Vamos verificar:

Lembre -se de que aquele derivado de uma constante é 0. Portanto, para o termo x⁴ Você pode adicionar qualquer constante e seu derivado continuará sendo 4x³.

Conclui -se que qualquer função da forma geral F (x) = x⁴ + C, onde C é uma constante real, serve como antiderivada de f (x).

O exemplo ilustrativo anterior pode ser expresso da seguinte maneira:

df (x) = 4x³ Dx

O antiderivado ou integral indefinido é expresso com o símbolo ∫, portanto:

F (x) = ∫4x³ dx = x⁴ + C

Onde a função f (x) = 4x³  se denomina integração, e C é o Constante de integração.

[TOC]

Exemplos de antiderivativos

figura 1. O anti -Hotley nada mais é do que uma integral indefinida. Fonte: Pixabay.

Encontrar um antiderivado de uma função é simples em alguns casos em que os derivados são bem conhecidos. Por exemplo, seja a função f (x) = sen x, um não -bidal.

Essa função pode ser:

F (x) = - cos x

Vamos verificar se é verdade:

F '(x) = (- cos x)' =- (-sen x) = sin x x

Portanto, podemos escrever:

∫sen x dx = -Cos x + c

Além de conhecer os derivados, existem regras básicas e simples de integração para encontrar antiderivados indefinidos ou integrais.

Pode atendê -lo: derivados sucessivos

Seja uma verdadeira constante, então:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Se uma função H (x) puder ser expressa como a soma ou subtração de duas funções, sua integral indefinida é:

3.- ∫h (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Esta é a propriedade da linearidade.

O Regra de energia Para integrais, ele pode ser estabelecido dessa maneira:

Esta regra tem uma restrição óbvia: desde o denominador N +1 Não pode ser feito 0, portanto n ≠ -1.

No caso de n = -1, a seguinte regra é usada:

5.- ∫x ^-1 Dx = ln x +c

É fácil demonstrar que o derivado de ln x é precisamente x ^-1.

Equações diferenciais

Uma equação diferencial é aquela em que o desconhecido é como um derivado.

Agora, a partir da análise anterior, é fácil perceber que a operação inversa ao derivado é o antiderivado ou integral indefinido.

Seja f (x) = y '(x), isto é, derivado de uma certa função. Podemos usar a seguinte notação para indicar este derivado:

Segue -se imediatamente que:

dy = f (x) dx

O desconhecido da equação diferencial é a função y (x), aquela cuja derivada é f (x). Para esclarecer, a expressão anterior é integrada em ambos os lados, o que equivale a aplicar o antiderivativo:

∫dy = ∫f (x) dx

A integral esquerda é resolvida pela regra de integração 1, com k = 1 e, portanto, o procurado -awaite é liberado:

e (x) = ∫f (x) dx = f (x) + c

E como C é uma constante real, para saber qual é apropriado em cada caso, a declaração deve conter informações adicionais suficientes para calcular o valor de C. Isso é chamado Condição inicial.

Veremos exemplos de aplicação de tudo isso na próxima seção.

Pode atendê -lo: estimativa pontual

Exercícios de Antiderivados

- Exercício 1

Aplique as regras de integração para obter os seguintes antiderivativos ou integrais indefinidos das funções dadas, simplificando os resultados o máximo possível. É conveniente verificar o resultado pela derivação.

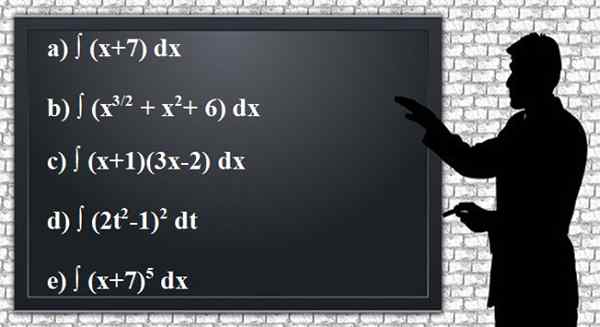Figura 2. Exercícios anterivados ou integrais definidos. Fonte: Pixabay.

Solução para

Aplicamos primeiro a regra 3, já que a integração é a soma de dois termos:

∫ (x +7) dx = ∫ xdx +∫7dx

Para a primeira integral, a regra dos poderes é aplicada:

∫ xdx = (x² /2)+C₁

Na segunda regra integral 1 se aplica, sendo k = 7:

∫7dx = 7∫dx = 7x + c₂

E agora os resultados são adicionados. As duas constantes são agrupadas em uma, genericamente chamada C:

∫ (x+7) dx = (x² /2) + 7x + c

Solução b

Por linearidade, esta integral se decompõe em três integrais mais simples, às quais a regra dos poderes será aplicada:

∫ (x^3/2 + x² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Observe que, para cada integral, uma constante de integração aparece, mas eles se reúnem em uma única chamada C.

Solução c

Nesse caso, é conveniente aplicar a propriedade distributiva da multiplicação para desenvolver a integração. Então você usa a regra dos poderes para encontrar cada integral separadamente, como no ano anterior.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) DX

O leitor atento observará que os dois termos centrais são semelhantes, portanto são reduzidos antes da integração:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Solução e

Uma maneira de resolver a integral seria desenvolver poder, como foi feito no Exemplo D. No entanto, como o expoente é maior, seria necessário fazer uma mudança variável, para não ter que fazer um desenvolvimento tão longo.

Pode atendê -lo: variável aleatória contínua

A mudança variável é a seguinte:

U = x + 7

Derivando de ambos os lados esta expressão:

du = dx

A integral é transformada para uma mais simples com a nova variável, que é resolvida com a regra de poderes:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Finalmente, a mudança é devolvida para retornar à variável original:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Exercício 2

Uma partícula está inicialmente em repouso e se move ao longo do eixo x. Sua aceleração para t> 0 é dada pela função a (t) = cos t. Sabe -se que em t = 0, a posição é x = 3, tudo em unidades do sistema internacional. É solicitado a encontrar a velocidade v (t) e a posição x (t) da partícula.

Solução

Como a aceleração é a primeira derivada da velocidade em relação ao tempo, você tem a seguinte equação diferencial:

a (t) = v '(t) = cos t

Segue que:

v (t) = ∫ cos t dt = sin t + c₁

Por outro lado, sabemos que a velocidade é, por sua vez, a derivada da posição, portanto, integramos novamente:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

As constantes de integração são determinadas a partir das informações fornecidas na declaração. Primeiro, ele diz que a partícula estava inicialmente em repouso, portanto v (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Então você tem que x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + c₂ = 3 → C₂ = 3+1 = 4

As funções de velocidade e posição são definitivamente assim:

v (t) = sen t

x (t) = - cos t + 4

Referências

1. Engler, a. 2019. Cálculo integral. Universidade Nacional da Costa.
2. Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.
3. Textos de matemática gratuitos. Antiderivativos. Recuperado de: matemática.Liibretexts.org.
4. Wikipedia. Antiderivativo. Recuperado de: em.Wikipedia.org.
5. Wikipedia. Integração indefinida. Recuperado de: é.Wikipedia.org.