Definição média de velocidade angular e fórmulas, exercícios resolvidos

O Velocidade angular média de rotação é definida como o ângulo girado pela posição da unidade de tempo do vetor de um ponto que descreve o movimento circular. As lâminas de um ventilador de teto (como o mostrado na Figura 1), seguem o movimento circular e sua velocidade angular média de rotação é calculada tomando a proporção entre o ângulo virado e o tempo em que esse ângulo foi percorrido.

As regras seguidas pelo movimento de rotação são de uma certa maneira semelhante aos parentes do movimento translacional. As distâncias percorridas também podem ser medidas em metros, no entanto, as magnitudes angulares assumem relevância especial porque facilitam bastante a descrição do movimento.

figura 1. Blades de ventilador têm velocidade angular. Fonte: Pixabay

Cartas gregas são geralmente usadas para magnitudes angulares e letras latinas para as magnitudes lineares correspondentes.

[TOC]

Definição e fórmulas

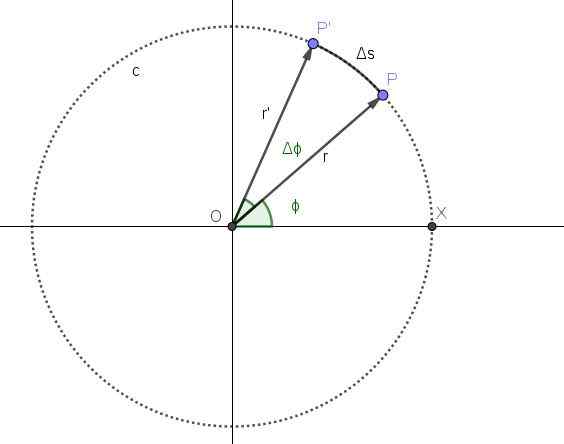
A Figura 2 representa o movimento de um ponto em uma trajetória circular c. A posição P do ponto corresponde ao instante t e a posição angular correspondente a esse momento é ϕ. 

A partir do momento em que um período de tempo é decorrido Δt. Nesse período, a nova posição do ponto é P 'e a posição angular aumentou um ângulo Δϕ.

Figura 2. Movimento circular de um ponto. Fonte: Self feito

A velocidade angular média ω é o ângulo percorrido por unidade de tempo, de modo que o quociente Δϕ/Δt represente a velocidade angular média entre os momentos t e t+Δt:

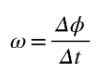
Como o ângulo é medido em radianos e tempo em segundos, a unidade da velocidade angular média é rad/s. Se você quiser calcular o velocidade angular Na época t, então o quociente Δϕ/Δt terá que ser calculado quando Δt ➡0.

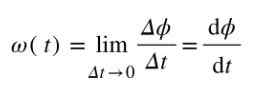A unidade de medida de velocidade angular instantânea também é rad/s.

Pode atendê -lo: os 31 tipos de força na física e suas características

Rotação uniforme

Um movimento de rotação é uniforme se a qualquer momento observado, o ângulo percorrido é o mesmo no mesmo período de tempo. Se a rotação for uniforme, a velocidade angular a qualquer momento coincide com a velocidade angular média.

Em um movimento de rotação uniforme, o tempo em que uma curva completa é chamado é chamado período E é indicado com t. 

Além disso, quando o ângulo percorrido está cheio, é 2π, portanto, em uma rotação uniforme, a velocidade angular ω está relacionada ao período T, pela seguinte fórmula:

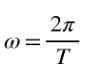
O frequência F de uma rotação uniforme, como a proporção entre o número de voltas e o tempo gasto em viajá -las, ou seja, no tempo em que Δt existe então a frequência será:

F = n/Δt

Como uma volta (n = 1), é percorrida em um tempo t (o período), o seguinte relacionamento está disponível:

F = 1/t

Ou seja, em uma rotação uniforme, a velocidade angular está relacionada à frequência através do relacionamento:

Ω = 2π ・ f

Relação entre velocidade angular e velocidade linear

Velocidade linear v, É o quociente entre a distância percorrida e o período de tempo usado para viajá -lo. Na Figura 2, a distância percorrida é o comprimento do arco ΔS. 

O arco ΔS é proporcional ao ângulo percorrido Δϕ e o Radio R, cumprindo o seguinte relacionamento:

ΔS = r ・ δϕ

Sempre que Δϕ é medido em radianos.

Se dividirmos a expressão anterior entre o período ΔT, obteremos:

(ΔS/ΔT) = r ・ (Δϕ/Δt)

A proporção de primeiro membro é a velocidade linear e o quociente do segundo membro, a velocidade angular média:

Pode atendê -lo: Mount Olympus (Marte)

v = r ・ ω

Exercícios resolvidos

-Exercício 1

As pontas das lâminas do ventilador do telhado mostradas na Figura 1 se movem com uma velocidade de 5 m/se as lâminas são 40 cm de raio.

Com estes dados calcular: i) a velocidade angular média da roda, ii) o número de voltas que a roda fornece em um segundo, iii) o período em segundos.

Solução 

i) A velocidade linear é v = 5 m/s.

O rádio é r = 0,40 m.

A partir da relação entre velocidade linear e velocidade angular, limpamos o último:

v = r ・ ω => ω = v/r = (5 m/s)/(0,40 m) = 12,57 rad/s

ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 Turn / s

iii) t = 1 / f = 1 / (2 turno / s) = 0,5 s por volta.

-Exercício 2

Um passeio de brinquedo se move em uma pista circular de 2M de raio. AS 0S, sua posição angular é 0 rad, mas depois de um tempo t, sua posição angular é

φ (t) = 2 ・ t .

Com esses dados 

i) Calcule a velocidade angular média nos intervalos de tempo seguinte [0s, 0.5s]; [0.5s, 1.0s]; [1.0, 1.5s] e finalmente no período [0.0, 1.5s]. 

ii) com base nos resultados da Parte I) o que pode ser dito sobre o movimento?

iii) Determine a velocidade linear média no mesmo período da Seção I)

iv) Encontre velocidade angular e velocidade linear para qualquer momento.

Solução 

i) A velocidade angular média é dada pela seguinte fórmula:

Continuamos a calcular o ângulo percorrido e o período de tempo decorrido em cada intervalo.

Intervalo 1: Δϕ = ϕ (0.5s) - ϕ (0.0s) = 2 (rad/s)*0.5s - 2 (rad/s)*0.0s = 1.0 rad

                   Δt = 0.5s - 0.0s = 0.5s

Pode atendê -lo: BTU (unidade térmica): equivalências, usos, exemplos

                   Ω = Δϕ/Δt = 1.0RAD/0.5s = 2.0 rad/s

Intervalo 2: Δϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad/s)*1.0s - 2 (rad/s)*0.5s = 1.0 rad

                   Δt = 1.0s - 0.5s = 0.5s

                   Ω = Δϕ/Δt = 1.0RAD/0.5s = 2.0 rad/s

Intervalo 3: Δϕ = ϕ (1.5s) - ϕ (1.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*1.0s = 1.0 rad

                   Δt = 1.5s - 1.0s = 0.5s

                   Ω = Δϕ/Δt = 1.0RAD/0.5s = 2.0 rad/s

Intervalo 4: Δϕ = ϕ (1.5s) - ϕ (0.0s) = 2 (rad/s)*1.5s - 2 (rad/s)*0.0s = 3.0 rad

                   Δt = 1.5s - 0.0s = 1.5s

                   Ω = Δϕ/Δt = 3.0RAD/1.5s = 2.0 rad/s

ii) Tendo em vista os resultados anteriores, nos quais a velocidade angular média foi calculada em diferentes intervalos de tempo, o mesmo resultado é sempre obtido. Parece indicar que é um movimento circular uniforme. No entanto, esses resultados não são conclusivos.

A maneira de garantir a conclusão é calcular a velocidade angular média para um intervalo arbitrário [t, t -t)

                                     Δt = t ' - t

                                     Ω = Δϕ/Δt = 2*(t'-t)/(t'-t) = 2.0 rad/s

Isso significa que o passeio de brinquedo tem uma velocidade angular média constante de 2 rad/s em qualquer período de tempo considerado. Mas você pode ir além se a velocidade angular instantânea for calculada:

Isso é interpretado como o carro de brinquedo o tempo todo, tem velocidade angular constante = 2 rad/s.

Referências

1. Giancoli, d. Física. Princípios com aplicações. 6ª edição. Prentice Hall. 30-45.
2. Kirkpatrick, l. 2007. Física: uma olhada no mundo. 6^ta Edição abreviada. Cengage Learning. 117.
3. Resnick, r. (1999). Físico. Volume 1. Terceira edição em espanhol. México. Empresa Editorial Continental S.PARA. claro.V. 33-52.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Edição. México. Editores de aprendizado do Cengage. 32-55.
5. Wikipedia. Velocidade angular. Recuperado de: Wikipedia.com