Definição de velocidade angular, fórmula, cálculo e exercícios

O velocidade angular É uma medida da velocidade de rotação e é definido como o ângulo que gira o vetor de posição do objeto que gira, por unidade de tempo. É uma magnitude que descreve muito bem o movimento de muitos objetos que constantemente giram em todos os lugares: CDs, rodas de carro, máquinas, terra e muito mais.

Um esquema do "London Eye" pode ser visto na figura a seguir. Representa o movimento de um passageiro representado pelo ponto P, que segue a trajetória circular, chamada C:

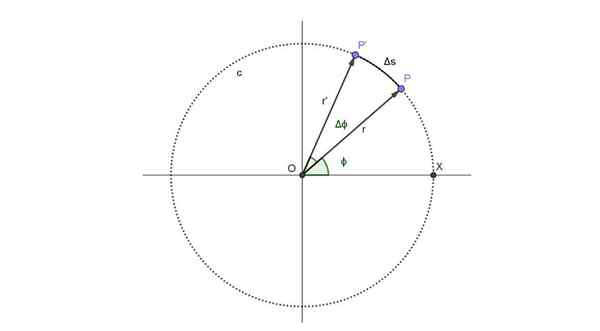Representação esquemática da trajetória circular que segue um passageiro do "London Eye". Fonte: Self feito.

O passageiro ocupa a posição P no instante t e a posição angular correspondente a esse momento é ϕ.

A partir do momento em que um período de tempo é decorrido Δt. Nesse período, a nova posição do passageiro pontual é P 'e a posição angular aumentou um ângulo Δϕ.

[TOC]

Como a velocidade angular é calculada ?

Para magnitudes rotacionais, letras gregas são amplamente utilizadas, a fim de diferenciá -las de magnitudes lineares. Então, inicialmente, a velocidade angular média ω é definida_m como o ângulo viajava em um determinado período de tempo.

Então o quociente Δϕ/Δt representará a velocidade angular média ω_m Entre os momentos T e T+ΔT.

Se você quiser calcular o velocidade angular Na época t, o quociente Δϕ/Δt terá que ser calculado quando Δt ➡0:

 A unidade de medida de velocidade angular é rad/s.

Relação entre velocidade linear e angular

Velocidade linear v, É o quociente entre a distância percorrida e o período de tempo usado para viajá -lo.

Na figura acima, a rota do arco é ΔS. Mas esse arco é proporcional ao ângulo percorrido e o raio, cumprindo o seguinte relacionamento, que é válido desde que Δϕ seja medido em radianos:

Pode servir a você: Método do paralelogramo: Exemplos, exercícios resolvidos

ΔS = r ・ δϕ

Se dividirmos a expressão anterior entre o período Δt e tomarmos o limite quando Δt ➡0, obteremos:

v = r ・ ω

Movimento de rotação uniforme

A foto é o famoso “London Eye”, uma roda de 135 m de alta rotativa que gira lentamente, para que as pessoas possam embarcar nas cabines em sua base e apreciar a paisagem de Londres. Fonte: Pixabay.

Um movimento de rotação é uniforme se a qualquer momento observado, o ângulo percorrido é o mesmo no mesmo período de tempo.

Se a rotação for uniforme, a velocidade angular a qualquer momento coincide com a velocidade angular média.

Em um movimento de rotação uniforme, o tempo em que uma curva completa é chamada de período e denota com t.

Além disso, quando o ângulo é girado, é 2π (equivalente a 360º). É por isso que, em uma rotação uniforme, a velocidade angular ω está relacionada ao período t, por meio da seguinte fórmula:

A frequência é definida F de uma rotação uniforme, como o quociente entre o número de voltas e o tempo gasto em viajar. Como 1 retorno, ele está viajando em um tempo t (o período) tem o seguinte relacionamento:

F = 1/t

Em outras palavras, em uma rotação uniforme, a velocidade angular está relacionada à frequência por:

Ω = 2π ・ f

Exercícios de velocidade angular resolvidos

Exercício 1

As cabines da grande roda rotativa conhecida como "London's Eye"Eles se movem lentamente. A velocidade das cabines é de 26 cm/se a roda tem 135 m de diâmetro.

Com esses dados, calcule:

Pode servir você: sol

i) a velocidade angular da roda

ii) a frequência de rotação

iii) o tempo que leva uma cabine para se virar.

Respostas:

Yo) A velocidade v em m/s é: v = 26 cm/s = 0,26 m/s.

O rádio é metade do diâmetro: r = (135 m) / 2 = 67,5 m

v = r ・ ω => ω = v/r = (0,26 m/s)/(67,5 m) = 0,00385 rad/s

Ii) Ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10^-4 turnos/s

F = 6,13 x 10^-4 Turn/s = 0,0368 Turn/min = 2,21 Turn/Hour.

Iii) T = 1 / f = 1/21 turn / hora = 0,45311 tempo = 27 min 11 seg

Exercício 2

Um carro de brinquedo se move em uma pista circular de 2m de raio. Aos 0 s, sua posição angular é 0 rad, mas depois de um tempo t, sua posição angular é dada por:

φ (t) = 2 ・ t 

Determinar:

i) velocidade angular 

ii) velocidade linear a qualquer momento.

Respostas:

Yo) A velocidade angular é o derivado da posição angular: ω = φ '(t) = 2.

Em outras palavras.

Ii) A velocidade linear do carro é: v = r ・ ω = 2 m ・ 2 rad/s = 4 m/s = 14,4 km/h

Exercício 3

O mesmo carro do exercício anterior começa a parar. Sua posição angular em função do tempo é dada pela seguinte expressão:

φ (t) = 2 ・ t - 0,5 ・ t² 

Determinar:

i) velocidade angular a qualquer momento

ii) velocidade linear a qualquer momento

iii) o tempo que você leva para parar do momento em que começa a desacelerar

iv) O ângulo viajou 

v) à distância percorrida

Respostas:

Yo) A velocidade angular é o derivado da posição angular: ω = φ '(t)

Ω (t) = φ '(t) = (2 ・ t - 0,5 ・ t²) '= 2 - T

Ii) A velocidade linear do carro a qualquer momento é dada por:

v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t

Pode atendê -lo: velocidade relativa: conceito, exemplos, exercícios

Iii) O tempo que leva no momento em que começa a desacelerar.

v (t) = 4 - 2 t = 0 => t = 2

Ou seja, ele para 2 s depois de começar a parar.

4) No período de 2s, desde o momento em que começa a parar até que um ângulo dado por φ (2) seja percorrido:

φ (2) = 2 ・ 2 - 0,5 ・ 2^2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 graus

V) No período de 2 s entendidos desde que começa a parar até parar uma distância dada por:

S = r ・ φ = 2m ・ 2 rad = 4 m

Exercício 4

As rodas de um carro têm 80 cm de diâmetro. Se o carro se mover a 100 km/h. Encontre: i) A velocidade angular da rotação da roda, ii) a frequência de rotação das rodas, iii) o número de voltas que a roda fornece em uma rota de 1 hora.

Respostas:

Yo) Em primeiro lugar, giraremos a velocidade do carro de km/h a m/s

V = 100 km / h = (100/3.6) m/s = 27,78 m/s

A velocidade angular de rotação das rodas é dada por:

Ω = v/r = (27,78 m/s)/(0,4 m) = 69,44 rad/s

Ii) A frequência de rotação da roda é dada por:

F = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 Turn / s

A frequência de rotação é geralmente expressa em revoluções por minuto r.p.m.

F = 11,05 Turn/s = 11,05 Turn/(1/60) min = 663,15 r.p.m

Iii)  O número de voltas que a roda fornece em uma rota de 1 hora é calculada sabendo que 1 hora = 60 min e que a frequência é o número de voltas n divididas pelo tempo em que esses n são dados.

F = n / t => n = f ・ t = 663,15 (voltas / min) x 60 min = 39788,7 turnos.

Referências

1. Giancoli, d. Física. Princípios com aplicações. 6ª edição. Prentice Hall. 106-108.
2. Resnick, r. (1999). Físico. Volume 1. Terceira edição em espanhol. México. Empresa Editorial Continental S.PARA. claro.V. 67-69.
3. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Edição. México. Editores de aprendizado do Cengage. 84-85.
4. Geogebra.org