Definição, Condições, Exercícios de Vetores não -coplanares

O Vetores não -coplanários Eles são aqueles que não compartilham o mesmo avião. Dois vetores livres e um ponto definem um único avião. Um terceiro vetor pode ou não compartilhar esse plano e, se não o fizer, esses não são vetores não -coplanares.

Os vetores não cúpulas não podem ser representados em espaços bilimensionais, como uma placa ou uma folha de papel, porque alguns deles estão contidos na terceira dimensão. Para representá -los adequadamente, você precisa usar a perspectiva.

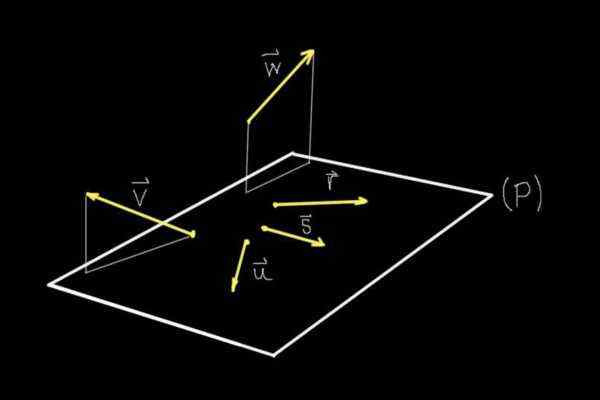figura 1. Coplanares e vetores não acopladores. (Elaboração própria)

Se observarmos a Figura 1, todos os objetos mostrados estritamente estão no plano da tela, no entanto, graças à perspectiva que nosso cérebro é capaz de imaginar um plano (P) que sai do mesmo.

Nesse avião (P) estão os vetores r, s, ou, enquanto vetores v e C  Eles não estão naquele avião.

Portanto, os vetores r, s, ou Eles são coplanarios ou coplanares entre si, pois compartilham o mesmo plano (P). Os vetores v e C Eles não compartilham um apartamento com nenhum dos outros vetores mostrados, portanto, eles não são acopladores. 

[TOC]

Coplanares e vetores de equações planas

Um avião é definido exclusivamente se três pontos forem apresentados no espaço tridimensional.

Suponha que esses três pontos sejam o ponto PARA, o ponto B e o ponto C que define o avião (P). Com esses pontos, é possível construir dois vetores AB = U e AC = v que são por construção com o avião (P).

O produto vetorial (ou produto cruzado) desses dois vetores resulta em um terceiro vetor perpendicular (ou normal) para eles e, portanto, perpendicular ao plano (P):

n = u X v   => n ⊥ ou  e n ⊥ v   => n ⊥ (P)    

Pode servir a você: Peso (físico): cálculo, unidades, exemplos, exercícios

Qualquer outro ponto que pertence ao avião (P) deve cumprir que o vetor Aq ser perpendicular ao vetor n; Isso é equivalente a dizer que o produto escalar (ou produto pontual) de n com Aq Deve ser zero:

n • Aq = 0 (*)

A condição anterior é equivalente a dizer que:

Aq • (ou X v) = 0 

Esta equação garante que o ponto Q pertencer ao avião (P). 

Equação cartesiana do avião

A equação anterior pode ser escrita de maneira cartesiana. Para isso, escrevemos as coordenadas dos pontos PARA, Q e os componentes do vetor normal n:

A = (a, b, c)

Q = (x, y, z)

n= (NX, NY, NZ)

Para que os componentes da AQ sejam:

Aq= (X-A, Y-B, Z-C)

A condição para o vetor Aq estar contido no avião (P) É a condição (*) que agora está escrita assim:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Cálculo do produto Point permanece:

nx (x-a) + ny (y-b) + nz (z-b) = 0

Se desenvolver e reorganizar, permanece:

nx x + ny y + nz z = nx a + ny b + nz c

A expressão anterior é a equação cartesiana de um plano (P), dependendo dos componentes de um vetor normal para (P) e as coordenadas de um ponto PARA que pertence a (P).

Condições para três vetores não serem não -coplanários

Como a condição foi vista na seção anterior Aq • (ou X v) = 0 garante que o vetor Aq É coplanario a ou e v.

Se ligarmos C para o vetor Aq Então podemos afirmar que:

C, ou e v Eles são coplanares, sim e somente se C • ( ou X v ) = 0.

Condição de não comportamento

Se o produto triplo (ou produto misto) de três vetores for diferente de zero, esses três vetores não são cobertos.

Pode servir a você: processo político: características, aplicações e exemplos

Sim    C • ( ou X v ) ≠ 0 Então os vetores u, v e w são não-couplanarios.

Se os componentes cartesianos dos u, v, v e w forem introduzidos, a condição de não-comportamento puder ser escrita da seguinte forma:

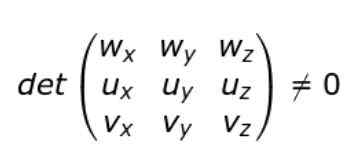Ou seja, se o determinante da matriz (3 × 3) cujas linhas são os componentes dos vetores u, v e w, então os vetores são não acopladores.

O produto triplo possui uma interpretação geométrica e representa o volume do paralelepipe gerado pelos três vetores não -coplanários.

Figura 2. Três vetores não acopladores definem um paralelepípedes cujo volume é o módulo de produto triplo. (Elaboração própria)

O motivo é o seguinte; Quando dois dos vetores que não são de acoplamento são multiplicados. 

Então, quando este vetor é multiplicar. 

Em outras palavras, você tem a área de paralelograma gerada pelos dois primeiros multiplicados pela altura do terceiro vetor.

Condição alternativa de não acoplamento

Se você tem três vetores e algum deles não pode ser escrito como uma combinação linear dos outros dois, os três vetores não são cobertos. São três vetores ou, v e C Eles não são cobertos se a condição:

α ou + β v + γ C = 0

É cumprido apenas quando α = 0, β = 0 e γ = 0.

Exercícios resolvidos

-Exercício 1

Você tem três vetores

ou = (-3, -6, 2);   v = (4, 1, 0) e C = (-1, 2, z)

Observe que o componente z do vetor C É desconhecido.

Encontre o intervalo de valores que Z pode tomar para que seja garantido que os três vetores não compartilhem o mesmo plano.

Pode servir a você: Equilíbrio estável: conceito e exemplos

Solução 

Aplicamos novamente o critério do determinante da matriz formado pelas fileiras dos três vetores, dessa maneira permanecemos: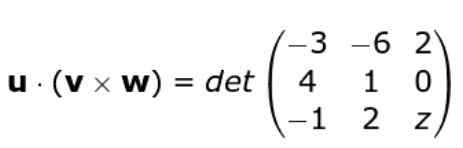Nós desenvolvemos o determinante

C • ( ou X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18

Combinamos essa expressão pelo valor zero

21 z + 18 = 0

E nós limpamos z

Z = -18/21 = -6/7

Se a variável Z assumisse o valor -6/7, os três vetores seriam coplanares.

Para que os valores de z que garantem que os vetores sejam não-cobertos são aqueles que estão no intervalo a seguir:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Exercício 2

Encontre o volume do paralelepípedo mostrado na figura a seguir:

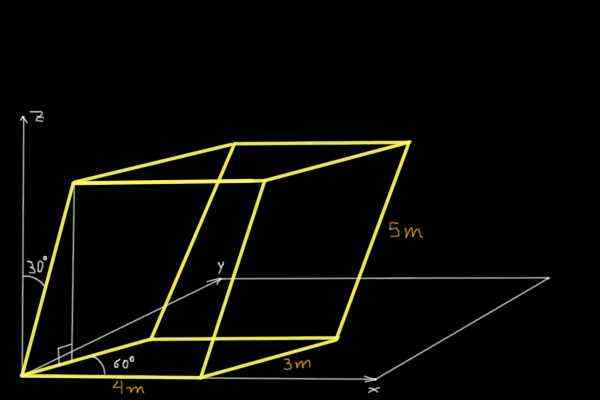
Solução 

Para encontrar o volume do paralelepípedo mostrado na figura, os componentes cartesianos de três vetores não-acopladores não concorrentes serão determinados na origem do sistema de coordenadas. O primeiro é o vetor ou  4m e paralelo ao eixo x:

ou= (4, 0, 0) m

O segundo é o vetor v No plano de tamanho XY de 3m que forma 60º com o eixo x:

v= (3*cos 60º, 3*sen 60º, 0) = (1.5, 2.6, 0.0) m

E o terceiro o vetor C de 5m e cuja projeção no plano XY forma 60º com o eixo x, além de W Formulário 30º com o eixo z.

C= (5*sin 30º*cos 60º, 5*sen 30º*sin 60º, 5*sen 30º)

Realizou os cálculos que temos: C= (1.25, 2.17, 2.5m.

Referências

1. Figueroa, d. Série: Física para Ciência e Engenharia. Volume 1. Cinemática. 31-68.
2. Físico. Módulo 8: vetores. Recuperado de: FRTL.Utn.Edu.ar
3. Hibbeler, R. 2006. Mecânica para engenheiros. Estático. 6ª edição. Empresa editorial continental.28-66.
4. McLean, w. Série Schaum. Mecânica para engenheiros: estático e dinâmico. 3ª edição. McGraw Hill. 1-15.
5. Wikipedia. Vetor. Recuperado de: é.Wikipedia.org