Conceito de velocidade relativa, exemplos, exercícios

O Velocidade relativa de um objeto é aquele que é medido em relação a um determinado observador, já que outro observador pode obter uma medida diferente. A velocidade sempre depende do observador que o mede.

Portanto, a velocidade de um objeto medido por uma determinada pessoa será a velocidade relativa em relação a ele. Outro observador pode obter um valor diferente para a velocidade, ainda no caso do mesmo objeto.

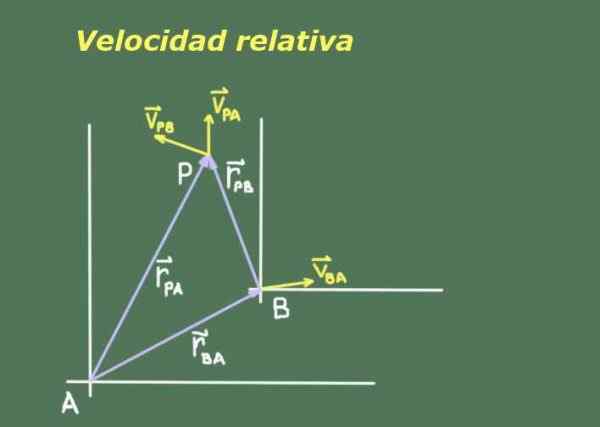
figura 1. Esquema que representa até o ponto P em movimento, visto dos sistemas de referência A e B. Fonte: Self feito.

Como dois observadores A e B que se movem um do outro, eles podem ter medidas diferentes de um terceiro objeto P que se move, é necessário procurar uma relação entre as posições e as velocidades das visualizações P por A e B.

A Figura 1 mostra dois observadores A e B com seus respectivos sistemas de referência, dos quais medem a posição e a velocidade do objeto P.

Cada observador A e B mede a posição e a velocidade do objeto P em um certo tempo t. Na relatividade clássica (ou galiliana), o tempo para o observador a é o mesmo que para o observador B, independentemente de suas velocidades relativas.

Este artigo trata da relatividade clássica válida e aplicável à maioria das situações cotidianas nas quais os objetos têm velocidades muito mais baixas do que a da luz.

A posição do observador B sobre os denota como r_BA. Como a posição é uma quantidade de vetor que usamos em negrito para indicá -la. A posição do objeto P em relação a um denota como r_PA e o do mesmo objeto P sobre B r_PB.

[TOC]

Relação entre posições e velocidades relativas

Existe uma relação vetorial entre essas três posições que pode ser deduzida da representação da Figura 1:

 r_PA= r_PB + r_BA

Se a expressão anterior for tomada em relação ao tempo t Obteremos a relação entre as velocidades relativas de cada observador:

Você pode atendê -lo: Segunda Lei de Newton: pedidos, experimentos e exercícios

V_PA= V_PB + V_BA

Na expressão anterior, existe a velocidade relativa de P em relação a um dependendo da velocidade relativa de P em relação a B e a velocidade relativa de B em relação a.

Da mesma forma, a velocidade relativa de P pode ser escrita em relação à velocidade relativa de P em relação a A e a velocidade relativa de B.

V_PB= V_PA + V_Ab

Deve -se notar que a velocidade relativa de B é igual e contrária à de B em relação a a:

V_Ab = -V_BA 

Isso é visto por uma criança de um carro em movimento

Um carro percorre uma estrada reta, que vai do oeste para isso, rapidamente a partir de 80 km/h enquanto na direção oposta (e na outra faixa) vem uma motocicleta rapidamente 100 km/h.

No banco traseiro do carro, viaja uma criança que quer conhecer a velocidade relativa de uma motocicleta que está se aproximando dele. Para descobrir a resposta, a criança aplicará os relacionamentos que você acabou de ler na seção anterior, identificando cada sistema de coordenadas da seguinte maneira:

-A é o sistema de coordenadas de um observador na estrada e, com relação a ele, os rapides de cada veículo foram medidos.

-B é o carro e P será a motocicleta.

Se você deseja calcular a velocidade do Moto P em relação ao carro B, o seguinte relacionamento será aplicado:

V_PB= V_PA + V_Ab=V_PA - V_BA

Tomando como positivo a direção oeste que você tem:

V_PB= (-100 km/h - 80 km/h) Yo = -180 km/h Yo

Este resultado é interpretado da seguinte maneira: a motocicleta se move em relação ao carro com uma velocidade de 180 km/h e direção -Yo, isto é, isso para o oeste.

Pode servir a você: Bloquear Álgebra: Elementos, Exemplos, Exercícios Resolvados

Velocidade relativa entre a motocicleta e o carro

A motocicleta e o carro cruzaram cada um seguindo sua pista. O garoto que entra no banco de trás do carro vê a motocicleta e agora quer saber em que velocidade ele se afasta dele, assumindo que tanto a motocicleta quanto o carro mantêm os mesmos rapides que antes de cruzar.

Para saber a resposta, a criança aplica o mesmo relacionamento que foi usado anteriormente:

V_PB= V_PA + V_Ab=V _PA - V_BA

V_PB= -100 km/h Yo - 80 km/h Yo = -180 km/h Yo

E agora a motocicleta se afasta do carro com a mesma velocidade relativa com que eles se aproximaram antes de cruzar.

A mesma motocicleta da Parte 2 retorna mantendo sua mesma velocidade de 100 km/h, mas alterando seu endereço. Ou seja, o carro (que continua rapidamente 80 km/h) e a motocicleta se move em uma direção positiva.

A certa altura, a motocicleta excede o carro, e a criança que entra no banco traseiro do carro quer conhecer a velocidade relativa da motocicleta em relação a ele quando ele a vê passar ao lado dela.

Para obter a resposta, a criança aplica novamente as relações do movimento relativo:

V_PB= V_PA + V_Ab=V_PA - V_BA

V_PB= +100 km/h Yo - 80 km/h Yo = 20 km/h Yo 

A criança do banco traseiro observa a motocicleta que avançava no carro com uma velocidade de 20 km/h.

-Exercício resolvido

Exercício 1

Um barco a motor atravessa um rio de 600 m de largura e fluindo de norte para sul. A velocidade do rio é de 3 m/s. A velocidade do barco em relação à água do rio é de 4 m/s a leste.

Pode atendê -lo: ramos da física clássica e moderna

(i) Encontre a velocidade do barco em relação à margem do rio.

(ii) indicar a velocidade e a direção do barco em relação à terra.

(iii) Calcule o tempo de cruzamento.

(iv) Quanto terá se mudado para o sul em relação ao ponto de partida.

Solução 

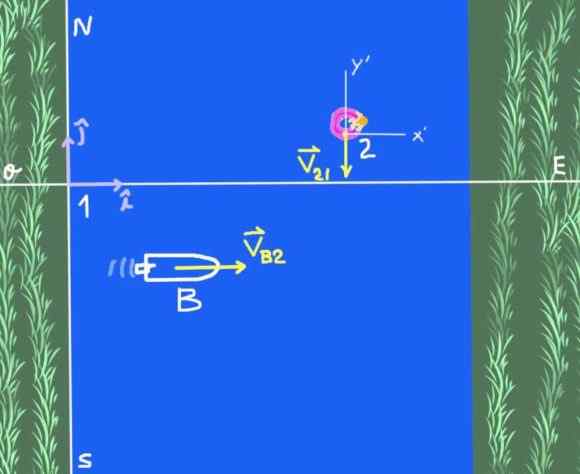Figura 2. Barco atravessando o rio (Exercício 1). Fonte: Self feito.

Existem dois sistemas de referência: o sistema de referência de solidariedade na margem do rio que chamaremos de 1 e o sistema de referência 2 que é um observador que flutua na água do rio. O objeto de estudo é o barco B.

A velocidade do barco em relação ao rio é escrita de forma vetorial da seguinte forma:

VB2 = 4 Yo EM

A velocidade do observador 2 (jangada sobre o rio) em relação ao observador 1 (na terra):

Vvinte e um = -3 J EM

Você quer encontrar a velocidade do barco em relação à terra VB1.

VB1 = VB2 + Vvinte e um

Resposta i

VB1 = (4 Yo - 3 J) EM   

A velocidade do barco será o módulo de velocidade anterior:

|VB1| = (42 + (-3) 2) ½ = 5 m/s

Resposta II

E o endereço será:

θ = arcan (-¾) = -36,87º 

Resposta III

O tempo de travessia do barco é a proporção entre a largura do rio e o componente X da velocidade do barco em relação à terra.

t = (600m)/(4 m/s) = 150 s 

Resposta IV

Para calcular a deriva que o barco tinha para o sul, o componente e a velocidade do barco em relação ao solo são multiplicados pelo tempo de cruzamento:

d = -3 J m/s * 150 s = -450 J m

O deslocamento para o sul em relação ao ponto de partida é de 450m.

Referências

1. Giancoli, d. Física. Princípios com aplicações. 6ª edição. Prentice Hall. 80-90
2. Resnick, r. (1999). Físico. Volume 1. Terceira edição em espanhol. México. Empresa Editorial Continental S.PARA. claro.V. 100-120.
3. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7º. Edição. México. Editores de aprendizado do Cengage. 95-100.
4. Wikipedia. Velocidade relativa. Recuperado de: Wikipedia.com
5. Wikipedia. Método de velocidade relativa. Recuperado de: Wikipedia.com