Definição, notação, exercícios de vetores de equipamentos

Dois ou mais vetores são equipamentos Se eles têm o mesmo módulo, a mesma direção e o igual sentido, mesmo quando seu ponto de origem é diferente. Lembre -se de que as características de um vetor são precisamente: origem, módulo, direção e sentido. 

Os vetores são representados por um segmento orientado ou de seta. A Figura 1 mostra a representação de vários vetores no avião, alguns dos quais são equipamentos de acordo com a definição inicialmente fornecida.

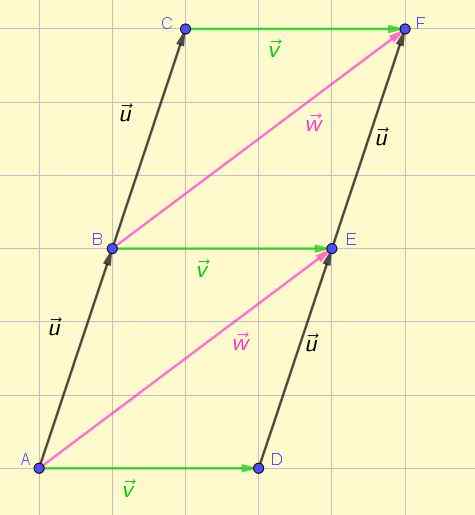figura 1. Equipamentos e vetores não equipados. Fonte: Self feito.

De uma primeira vista, é possível apreciar que os três vetores verdes tenham o mesmo tamanho, a mesma direção e o mesmo sentido. O mesmo pode ser afirmado sobre os dois vetores rosa e os quatro vetores negros.

Numerosas magnitudes da natureza têm um comportamento vetorial, esse é o caso de velocidade, aceleração e força, para citar apenas alguns. Daí a importância de caracterizá -los adequadamente.

[TOC]

Notação para vetores e equipamentos

Para distinguir as quantidades do vetor das quantidades escalares, a letra do tipo preto ou uma seta na letra é frequentemente usada. Ao trabalhar com vetores manuais, no caderno, é necessário distingui -los com a flecha e quando um meio impresso é usado, ousados ​​são usados.

Os vetores podem ser negados indicando seu ponto de partida ou origem e seu ponto de chegada. Por exemplo Ab, Bc, DE e Ef da Figura 1 são vetores, no entanto Ab, Bc, DE e Ef São quantidades escalares ou números que indicam a magnitude, módulo ou tamanho de seus respectivos vetores.

Para indicar que dois vetores são equipamentos, o símbolo é usado "∼ ". Com essa notação, na figura, podemos apontar os seguintes vetores que são equipamentos entre si:

Pode servir a você: energia cinética: características, tipos, exemplos, exercícios

AB∼BC ~DE ~ EF 

Todos eles têm a mesma magnitude, direção e significado. Portanto, cumpra os regulamentos indicados acima.

Vetores livres, deslizantes e opostos

Qualquer um dos vetores da figura (por exemplo Ab) é um representante do conjunto de todos os vetores fixos. Este conjunto infinito define a classe de vetores livres ou.

ou = Ab, bc, de, ef, ..

Uma notação alternativa é a seguinte:

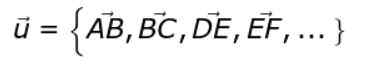
Se o ousado ou seta não for colocada no topo ou, Queremos nos referir ao módulo vetorial ou.

Vetores livres não são aplicados a algum ponto particular.

Por sua parte Vetores deslizantes Eles são equipamentos de equipamento para um determinado vetor, mas seu ponto de aplicação deve estar contido na linha de ação vetorial.

E os vetores opostos São vetores que têm a mesma magnitude e direção, mas sentidos opostos, embora em textos em inglês sejam chamados endereços opostos Como o endereço também indica o significado. Vetores opostos não são equipamentos.

Exercícios

-Exercício 1

Quais outros vetores dos mostrados na Figura 1 são equipamentos entre si?

Solução

Além dos já indicados na seção anterior, é observado na Figura 1 que DE ANÚNCIOS, Ser e EC Eles também são vetores de equipamentos entre si:

Ad ∼ ser ∼ CE 

Qualquer um deles é um representante da classe de vetores livres v.

Vetores também são equipamentos entre si Ae e BF :

Ae ∼ BF 

Quem são representantes de classe C.

-Exercício 2

Os pontos A, B e C estão no avião cartesiano XY e suas coordenadas são:

Pode atendê -lo: gás ideal: modelo, comportamento, exemplos

A = (-4,1), b = (-1,4) e c = (-4, -3)

Encontre as coordenadas de um quarto ponto D para que os vetores Ab e CD Ser equipamento.

Solução 

Para que CD ser equipamento Ab deve ter o mesmo módulo e a mesma direção que Ab .

O módulo de Ab Quadrado é:

|Ab|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D Coordenadas são desconhecidas pelo que podemos dizer: d = (x, y)

Então: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

AS |Ab| = |CD| É uma das condições para Ab e CD Ser equipamento que você tem:

(x + 4)^2 + (y + 3)^2 = 18

Como existem duas incógnitas, é necessária outra equação, que pode ser alcançada a partir da condição de que Ab e CD ser paralelo e no mesmo sentido.

Vector AB inclinação

A inclinação do vetor Ab indica seu endereço:

Pendente AB = (4 -1)/(-1 -( -4)) = 3/3 = 1

Indicando que o vetor Ab 45º forma com o eixo x.

Inclinação do vetor de CD

A inclinação de CD É calculado da mesma forma:

CD pendente = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Corresponder a este resultado com a inclinação de Ab Você tem a seguinte equação:

Y + 3 = x + 4 

O que significa y = x + 1.

Se esse resultado for substituído na equação da igualdade dos módulos, é:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Simplificar é:

2 (x+4)^2 = 18, 

Que é equivalente a:

(x+4)^2 = 9

Isto é x+4 = 3 que implica que x = -1. Para que as coordenadas de D sejam (-1, 0).

verificar

Componentes vetoriais Ab Eles são (-1-(-4); 4 -1) = (3; 3)

Pode servir a você: teorema do tevenin: o que consiste, aplicativos e exemplos

e os do vetor CD Eles são (-1-(-4)); 0 -(-3)) = (3; 3)

O que significa que os vetores são equipamentos. Se dois vetores tiverem os mesmos componentes cartesianos, têm o mesmo módulo e direção, portanto são equipamentos.

-Exercício 3

O vetor livre ou tem magnitude 5 e endereço 143.1301º.

Encontre seus componentes cartesianos e determine as coordenadas dos pontos B e C, sabendo que os vetores fixos AB e CD são equipamentos. As coordenadas de A são (0, 0) e as coordenadas do ponto C são (-3,2).

Solução 

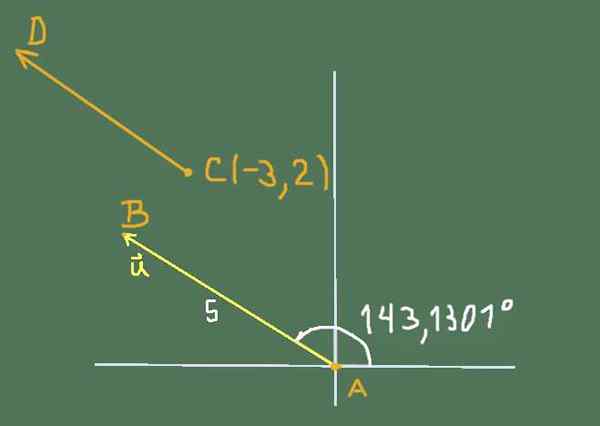
A situação proposta pelo exercício pode ser representada pela figura a seguir:

Figura 2. Diagrama para resolução do Exercício 3. Fonte: Self feito.

Componentes cartesianos de ou são

ou = (5*cos (143.1301º); 5*sin (143.1301º))) 

Fazendo os cálculos permanecem:

ou = (-4; 3) 

B Coordenadas são desconhecidas, então colocaremos B (x, y)

Coordenadas do vetor Ab Eles são (X-0; Y-0), mas como é o equipamento com U deve ser cumprido a igualdade de componentes, conclui-se que as coordenadas de B são (-4, 3).

Da mesma forma, o vetor coordena CD eles são (x-(-3)); (e - 2) que devem ser equipamentos u, lou isso leva a:

 x + 3 = -4 e y -2 = 3

Então as coordenadas do ponto D serão (-7, 5).

Referências

1. Cálculo.DC. Vetor fixo. Vetor livre. Recuperado de: cálculo.DC
2. 2d Descartes. Vetores fixos e vetores livres do avião. Recuperado de: Recursos.Educação.é
3. Projeto Guao. Vetores de equipo. Recuperado de: guao.org
4. Resnick, r., Krane, k. (2001). Física (em inglês). Nova York: John Wiley & Sons.
5. Serway, r.; Jewett, John W. (2004). Física para cientistas e engenheiros (em inglês) (6ª edição). Brooks/Cole.
6. Tupler, Paulo A. (2000). Física para Ciência e Tecnologia. Volume I. Barcelona: Ed. Eu revertei.
7. Weisstein, e. "Vetor". Em Weisstein, Eric W. Mathworld (em inglês). Pesquisa de Wolfram.