Variação proporcional

O que é variação proporcional?

A variação proporcional entre duas variáveis ​​"x" e "y" ocorre quando, multiplicando uma delas por uma constante, a outra também é multiplicada ou dividida pela mesma constante. Muitas situações do mundo real podem ser descritas adequadamente com eles.

A proporcionalidade entre as variáveis ​​pode ser direta ou inversa. Na proporcionalidade direta, o relacionamento é do tipo:

y = k ∙ x

Ou equivalente:

K = y/x

Onde k é uma constante chamada proporcionalmente constante qualquer proporção de proporcionalidade. Observe que se "x" aumentar, "y" faz isso na mesma proporção e, se "x" diminuir, ele também "y". Quando a relação entre as variáveis ​​é gráfica, é obtida uma linha reta que passa pela origem do sistema de coordenadas (consulte o exercício resolvido posteriormente).

A variação direta também pode ocorrer entre uma variável e um poder do outro, por exemplo, "y" pode ser diretamente proporcional a x², x³ e assim.

Por outro lado, na proporcionalidade inversa, as variáveis ​​estão ligadas através da expressão:

x ∙ y = k

Esta expressão significa que o produto das variáveis ​​é uma constante. Ao representar graficamente a relação entre as variáveis, é uma hipérbola. Além disso, se o produto de uma variável com um poder do outro for constante, também representa um caso de proporcionalidade reversa, por exemplo:

x²∙ y = k; x³∙ y = k ..

Exemplos

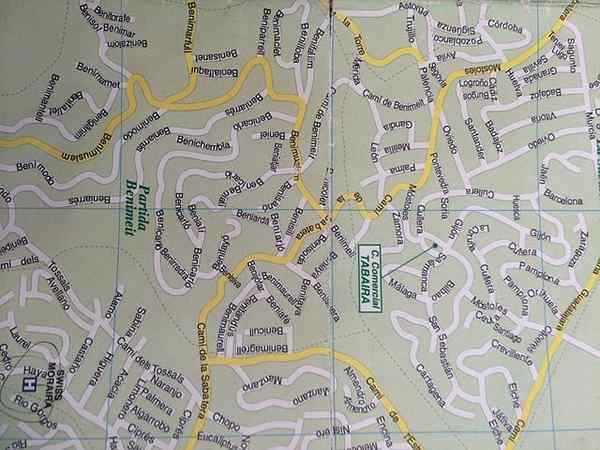Uma aplicação de variação proporcional é o layout de mapas

Muitas leis da física e química são expressas matematicamente como proporções. Por exemplo, a força que exerce uma mola e o alongamento do mesmo, a relação entre a pressão e o volume em um gás à temperatura constante, o período de um pêndulo simples e a raiz quadrada de seu comprimento e muito mais. Conhecendo o modelo que governa o fenômeno, você pode descobrir seu comportamento por qualquer valor das variáveis.

Pode atendê -lo: Teorema da existência e exclusividade: demonstração, exemplos e exercícios

E não apenas isso, eles também se aplicam em inúmeras situações como estas:

• Passe o padrão de uma roupa de um tamanho menor para um tamanho maior (ou vice -versa).
• Em fatores de conversão, para passar de uma unidade para outra, como quilômetros a quilômetros, galões a litros e mais.
• Calcule os ingredientes de uma receita para 6 pessoas conhecendo o requisito para 4 pessoas.
• Determinar o valor de certos impostos de acordo com a renda obtida.
• No cálculo do interesse simples.
• Ao desenhar aviões em escala.
• Quando você precisa calcular o preço de uma quantidade de produtos que conhecem o preço unitário.
• Na semelhança dos triângulos.

Em seguida, em detalhes, há duas situações interessantes em que as variações proporcionais se aplicam:

Exemplo 1

Na escala de uma cidade, a Hermitage Avenue mede 3.2 cm, sendo seu comprimento real de 400 m. Por outro lado, a rua de La Fuente, que realmente mede 180 m de comprimento, tem que desenhar com um derrame proporcionalmente mais curto. Qual é o tamanho do golpe?

A declaração oferece as informações completas da Avenida Ermita: deixe a duração real da avenida e seu comprimento no avião, pois a variação é de proporcionalidade direta, ela deve:

L = k ∙ ℓ

A partir dos dados sobre a Hermitage Avenue, você pode saber o valor da constante de proporcionalidade K, mas antes que seja necessário deixar todos os comprimentos nas mesmas unidades:

3.2 cm = 0.032 m

Então:

400 m = k ∙ 0.032 m

Portanto, a constante de proporcionalidade é:

Pode atendê -lo: quais são os elementos da parábola? (Peças)

K = 400 /0.032 = 12500

Agora se sabe que:

L = 12500 ∙ ℓ

Este resultado é interpretado da seguinte forma: o comprimento das ruas neste mapa é 12500 vezes menor que o seu comprimento real. Portanto, a linha da rua de La Fuente mede:

ℓ = 180 m/ 12500 = 0.0144 m = 1.44 cm

Exemplo 2

Um analista possui a tabela de valores a seguir para as variáveis ​​"X" e "Y" obtidas experimentalmente e quer saber se esses dados se encaixam em um modelo de variação proporcional direta ou de variação proporcional inversa.

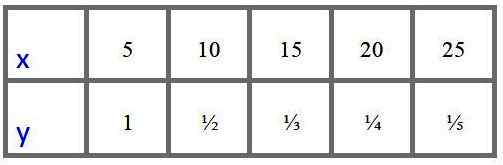
O que você deve fazer para saber?

Em primeiro lugar, observa -se que, quando "x" aumenta, "y" diminui, por isso suspeita que uma proporcionalidade reversa, em qualquer caso, para garantir que o analista tenha a opção de avaliar se o quociente e/x é constante (proporcional variação direta) ou se o produto x.e é constante (variação proporcional inversa).

Testando com a primeira opção:

1 ÷ 5 = 0.2

½ ÷ 10 = 0.05

⅓ ÷ 15 = 0.022 ..

Conclui -se que não é uma variação proporcional direta, porque o quociente e/x fornecem valores diferentes para cada par de dados.

Precisamos verificar se o produto x ∙ é constante:

5 × 1 = 5

10 × ½ = 5

15 × ⅓ = 5

20 × ¼ = 5

25 × ⅕ = 5

E como o produto x ∙ y = 5 conclui -se que a variação é de proporcionalidade reversa.

Esta informação serve para conhecer valores que não estão na tabela, por exemplo, qual seria o valor de "y" quando x = 30?

De x ∙ y = 5, “y” é limpo e substituído x = 30:

y = 5/x

y = 5/30 = 1/6

Exercício resolvido

Se um medidor de tecido custar 6.US $ 75, e sabendo que o preço é diretamente proporcional à quantidade de metros para comprar, encontre:

Pode servir a você: Antiderivativo: fórmulas e equações, exemplos, exercícios

a) A expressão algébrica que vincula as variáveis ​​"Preço em $" e "Número de metros de tecido".

b) Prepare uma tabela de valores com preços para 3, 6, 9, 12, 15 e 18 metros de tecido.

c) Graph os valores obtidos.

Responda para

Deixe o preço "y" da variável "em $" e "x" a variável "quantidade de metros de tecido". Como são diretamente proporcionais, você precisa:

y = k ∙ x

Para x = 1 metro, y = 6.US $ 75, portanto k = 6.75 $/medidor. Este é o preço unitário do tecido, o preço de qualquer outro tecido "X" é obtido multiplicando por esse valor; então, a expressão algébrica procurada é:

y = 6.75 ∙ x

Resposta b

A tabela de valores com preços a US $ 3, 6, 9, 12, 15 e 18 metros é:

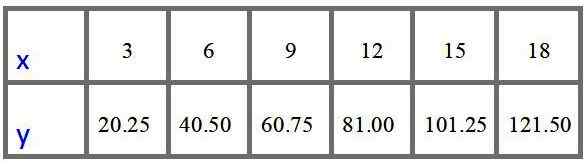
Resposta c

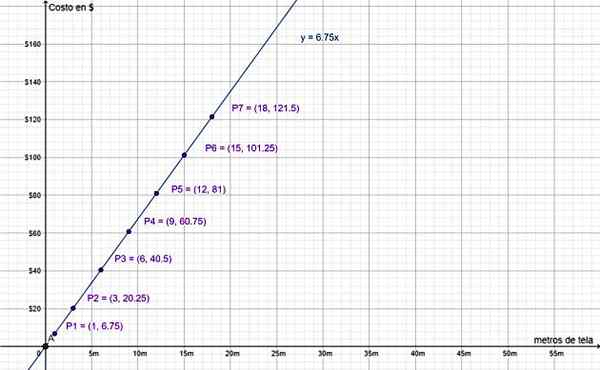
Finalmente, o gráfico dos valores na tabela anterior corrobora que é uma variação proporcional direta:

O custo a $ e a quantidade de metros de tecido são quantidades diretamente proporcionais. Fonte: f. Zapata.

Observe que o valor (0,0) está incluído, pois a linha y = 6.75 ∙ X passa pela origem do sistema de coordenadas, conforme explicado antes. Faz sentido, pois não fazer uma compra é equivalente à compra de 0 m de tecido, cujo valor é 0 $.

Referências

1. Larson, r. 2012. Pré-escultura. 8º. Edição. Cengage Learning.
2. Secretaria de Educação Pública do México. A variação proporcional. Recuperado de: PPS.K12.Ou.nós.
3. Stewart, J. 2007. Pré-cálculo: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
4. Unam. Guias de estudo: Matemática I. Recuperado de: Dirre.Unam.mx.
5. Zill, d. 2008. Pré-cálculo com avanços de cálculo. 4º. Edição. McGraw Hill.