Explicamos o que e quais são as medidas de dispersão, e damos vários exemplos

O que são medidas de dispersão?

As Medidas de dispersão ou de variação, nas estatísticas, meça quanto uma distribuição de dados do valor de uma medida central se move, como a média média ou aritmética. Seu valor é sempre positivo e normalmente diferente de 0, exceto no caso de dados idênticos.

Se uma medida de dispersão produz um pequeno valor, significa que os dados estão localizados muito próximos da média, mas se for grande, significa que os dados estão mais dispersos, portanto, longe da média.

As medidas de dispersão são muito importantes do ponto de vista estatístico, não apenas como indicadores aritméticos da variação de dados, mas como uma ajuda inestimável quando você deseja melhorar a qualidade, tanto na fabricação de produtos quanto na prestação de serviços.

Exemplo disso são as fileiras de atenção nos bancos. O tempo médio que atrasa os clientes quando eles fazem uma linha exclusiva e depois são distribuídos nas bilheterias, é o mesmo que se eles fizessem linhas individuais na frente de cada.

No entanto, a dispersão é menor na linha única, o que significa que o tempo de atenção individual é muito semelhante a cada cliente. Os clientes declararam que se sentem mais confortáveis ​​dessa maneira, mesmo que o tempo médio de atendimento seja o mesmo em ambas as modalidades.

Principais medidas de dispersão

Os principais são: classificação, variação, desvio padrão e coeficiente de variação.

Faixa

A classificação R de um conjunto de dados é definida para a diferença entre o valor máximo x_Máx e o valor mínimo x_min do todo:

Tocar = r = valor máximo - valor mínimo = x_Máx - x_min

Pode atendê -lo: quais são os números para? Os 8 principais usos

O intervalo é rápido em calcular, mas é muito sensível a valores extremos e tem a desvantagem de não levar em consideração valores intermediários. Portanto, é usado apenas para ter uma idéia inicial e aproximada da dispersão de dados.

Exemplo de classificação

Esta é uma lista do número de furacões no Atlântico durante os últimos 14 anos:

8; 9; 7; 8; quinze; 9; 6; 5; 8; 4; 12; 7; 8; 2

Os dados máximos de valor são 15 e o valor mínimo é 2, portanto:

R = valor máximo - valor mínimo = x_Máx - x_min = 15 - 2 = 13 furacões

Variação

Essa medida é usada para comparar cada um dos dados com a média do conjunto e é calculado adicionando as diferenças, quadradas de alta, entre cada valor com a média e a divisão pelo número total de valores.

Ser:

-A média: μ

-Qualquer valor, pertencente ao conjunto de dados: x_Yo

-O número total de observações: n

Denotando a variação de uma população como σ², A expressão para calculá -lo é:

E quando uma amostra de uma população é coletada, é preferido calcular a variação da seguinte maneira:

Onde a variação da amostra foi indicada com s e a média como x com barra, para deixar o uso de letras gregas na população. A razão para dividir entre N-1, em vez de n, é a variação da amostra para não subestimar a população, o que sempre acontece quando se divide entre n.

Por outro. Em vez disso, os quadrados são sempre positivos.

Pode servir a você: probabilidade de frequência: conceito, como é calculado e exemplos

Portanto, a variação é sempre positiva, mesmo que a diferença entre x_Yo E a média é negativa e sua principal vantagem da variação é que ele leva em consideração cada dados do conjunto.

Mas tem a inconveniência de que suas unidades não são as mesmas que as dos dados, por exemplo, se estes consistirem em tempos, medidos em minutos, a variação do conjunto será dada em minutos ao quadrado.

Exemplo de variação

O cálculo da variação requer encontrar a média. Tomando os dados do número de furacões, a média é calculada por:

(8 + 9 + 7+ 8 + 15 + 9 + 6 + 5+ 8 + 4 + 12 + 7 + 8+ 2)/14 = 7.7 furacões.Portanto, a variação é:

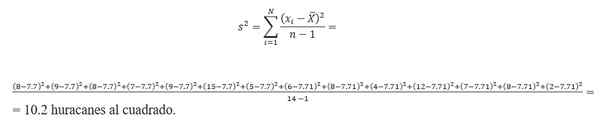
Desvio padrão

Para corrigir o problema da falta de concordância entre as unidades, o desvio padrão é definido σ, Como a raiz quadrada da variação:

E análoga, no caso de uma amostra:

Existe uma regra empírica para estimar o valor do desvio padrão de um conjunto de dados de amostra, com base no intervalo. De acordo com esta regra, o desvio padrão é aproximadamente um quarto de R:

S ≈ r/4

Tem a vantagem de permitir uma estimativa rápida do desvio padrão, pois as operações são muito mais simples.

O desvio padrão é, com muito, a medida de dispersão mais usada, por isso vale a pena destacar suas principais características:

• O desvio padrão indica quanto os dados da mídia se afastam
• É sempre positivo, mas pode ser 0 se todos os dados forem idênticos
• Quanto maior o valor do desvio padrão, mais dispersos são os dados
• As unidades de desvio padrão são as mesmas que as da variável em estudo
• Seu valor muda rapidamente quando um dos dados (ou mais) tem um valor muito diferente do resto
• Os valores de desvio padrão são tendenciosos, ou seja, as médias do desvio padrão não são distribuídas em torno da média, em contraste com a variação, que não é entregada.

Pode atendê -lo: Acutangle Triangle

Exemplo de desvio padrão

Continuando com o exemplo de furacões, o desvio padrão é:

Ou, se for preferido usar a abordagem do desvio padrão através do intervalo, é obtido um valor bastante próximo:

S = 13/4 = 3.25

Coeficiente de variação

O coeficiente de variação é indicado pelas iniciais CV ou R, em alguns textos e ambos para uma população e para uma amostra, relaciona o desvio padrão e médio, como uma porcentagem:

O bem:

As equações são válidas desde que a média seja diferente de 0.

Como regra, o coeficiente de variação é arredondado para um único decimal e é usado para comparar dados de duas populações diferentes.

Exemplo de coeficiente de variação

Os tempos de espera em segundos, para os clientes de um banco, são gravados em duas situações: quando eles fazem uma linha única e quando fazem classificações individuais antes da bilheteria de atenção. Os resultados são os seguintes:

Ambos os conjuntos de dados podem ser comparados através de seu respectivo coeficiente de variação:

Fila unica

• Média = 429 segundos
• Desvio = 28.6 segundos
• CV = (28.6/429) x 100 = 6.7 %

Classificações individuais

• Média = 429 segundos
• Desvio = 109.3 segundos
• CV = (109.3/429) x 100 = 25.5 %

Como esse último valor é maior, isso indica que há mais variabilidade nos tempos de atendimento ao cliente quando eles fazem classificações individuais do que quando fazem uma linha única, embora o tempo médio seja o mesmo em cada caso.