A rombóide É uma figura plana de quatro lados, um quadrilateral -em que seus lados e seus ângulos internos são diferentes dois a dois. Portanto, o romboide pertence ao grupo de paralelogramas oblíquos.

As figuras geométricas fazem parte da natureza e, em particular, as de quatro lados como o romboide, têm muitas aplicações em arquitetura e design.

figura 1. Os painéis de iluminação do Allianz Arena Stadium em Munique, Alemanha, iluminam com as cores da equipe local e com luz branca quando a seleção daquele país toca. Fonte: pxhere.

Up, temos parte da fachada do Allianz Arena Football Stadium em Munique. São painéis romboides que iluminam com as cores da equipe local.

É, portanto, uma figura com muito dinamismo visual, porque, diferentemente de outros quadriláteros, ele não tem eixo de simetria. A figura a seguir mostra vários romboides com orientações variadas no plano.

Figura 2. Vários romboides com diferentes orientações no plano. Fonte: f. Zapata.

[TOC]

Características romboides

Em seguida, as principais características desta interessante figura geométrica:

-Número da folha: 4.

-Número de vértices: 4.

-Os lados opostos são iguais e paralelos, no entanto, os lados adjacentes são desiguais.

-Possui 4 ângulos internos: dois agudos (menos de 90º), indicados pela letra grega α e dois obtusos (mais de 180º), chamados β (ver Figura 3).

-Ao adicionar dois ângulos contíguos do romboide, 180º é obtido, portanto α e β são Suplementar.

-A soma dos 4 ângulos internos é igual a 360º.

-Uma diagonal é um segmento que começa em um vértice e termina no vértice oposto.

-O ponto em que as diagonais do intersect romboide são chamadas BaryCenter.

-Os diagonais romboides têm tamanhos diferentes.

Sobre as diagonais do romboide, existem alguns detalhes importantes que discutiremos abaixo.

Pode atendê -lo: pendente de uma linha: fórmula e equações, representação, exemplos

Diagonais do romboide

É muito importante enfatizar que os diagonais dos romboides não são bisétricos, ou seja, eles não dividem os ângulos internos da figura em duas partes iguais.

As diagonais não são perpendiculares uma à outra. No entanto, podemos calculá -los facilmente com o teorema de cosseno. Assim, a principal diagonal D_M No romboide da Figura 3 está:

D_M = √ (A² + b² - 2.Ab.cos β)

E a menor diagonal d_m Eu gostaria:

D_m = √ (A² + b² - 2.Ab.cos α)

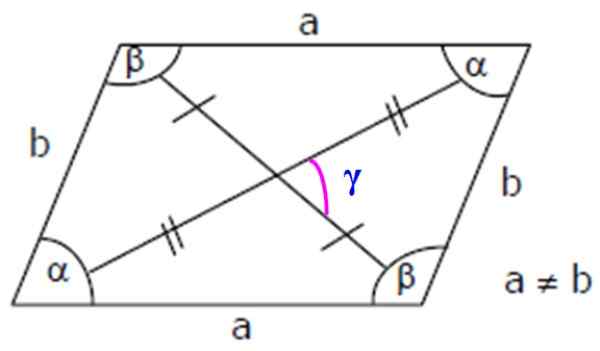Figura 3. Elementos romboides: lados, ângulos internos e diagonais. Fonte: Wikimedia Commons.

Importante: Como α e β são suplementares, é cumprido que:

sin α = sin β

cos α = -Cos β

Essas propriedades de razões trigonométricas devem ser levadas em consideração ao resolver os exercícios.

Como tirar o perímetro e a área

Para encontrar o perímetro e a área, daremos nome aos lados do romboide, estes serão para e b. Também temos a altura do romboide, chamado h, que é a linha extraída de um dos vértices e direcionada perpendicularmente ao lado oposto da figura.

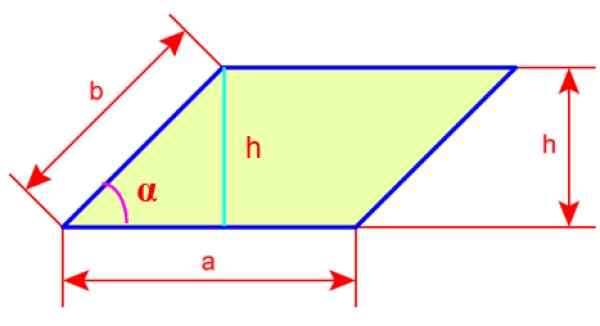Figura 4. Lados e altura romboid. Fonte: Wikimedia Commons.

Perímetro do romboide

O perímetro do romboide é calculado adicionando os comprimentos de seus quatro lados. Vamos ligar para P para o perímetro, então:

P = 2a + 2b

Também podemos expressá -lo através de:

P = 2 (a+b)

Perímetro sabendo a altura

Se olharmos bem, a altura h pode ser determinada a partir do triângulo à esquerda na Figura 4. O lado B seria a hipotenusa e a altura que o Cateto oposto ao ângulo α, portanto:

sin α = oposto / hipotenusa cateto

O bem:

sin α = h / b

Então limpamos B:

b = h / sin α

Substituímos no perímetro P:

P = 2 [a + (h / sin α)]

Área romboide

A área romboide é a medida de sua superfície. E como é um paralelogramo, sua área A é dada pela expressão bem conhecida:

Pode atendê -lo: fator comum para agrupar termos: exemplos, exercícios

A = base x altura

Que, de acordo com as Figuras 3 e 4, é expresso através de:

A = a x h

Área conhecendo os dois lados e um ângulo interno

Aplicando a trigonometria básica da seção anterior, encontramos expressões equivalentes para a área romboide:

h = b. sin α

Então a área é assim:

A = a. b. sin α

Lembrando o que dissemos acima sobre os ângulos suplementares, podemos substituir o sen α por sen β, se necessário.

Área conhecendo as diagonais e ângulo entre eles

Finalmente, se conhecemos as diagonais D_M e d_m, Além do ângulo γ entre eles (veja a Figura 3), a área pode ser calculada pelo semi -produto das diagonais através do seio do referido ângulo:

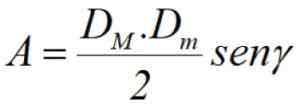
Exercício resolvido

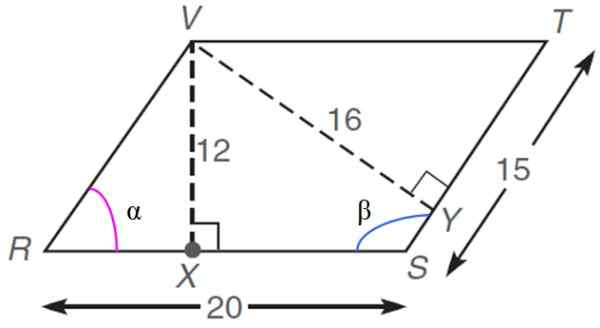
No romboide a seguir, cujas dimensões são dadas em unidades arbitrárias ou.para., encontrar:

a) o valor do perímetro

b) A área

c) ângulos internos α e β

d) o comprimento do segmento RX

e) a medida de cada uma das diagonais

Solução para

O perímetro P é:

P = 2 (a + b)

Identificamos primeiro os valores de A e B:

A = 20

B = 15

Substituímos a fórmula e calculamos:

P = 2. (20 + 15) = 70 u.para.

Solução b

O diagrama fornece altura h = 12 u.A, portanto, a área pode ser calculada com a fórmula:

A = a x h

A = 20 x 12 u.para.² = 240 u.para.²

Independentemente da unidade selecionada para medir os lados e a altura, a área é sempre expressa em unidades quadradas.

O mesmo resultado se você conseguir ao calcular a área com a outra altura do romboide, que vale 16 u.para. Em efeito:

A = 16 x 15 u.para.² = 240 u.para.²

Solução c

O ângulo α pode ser calculado através de:

Pode servir a você: medidas de posição, tendência central e dispersão

h = b. sin α

Como os valores H e B são conhecidos, portanto:

α = Arcsen (H/B) = Arcsen (12/15) = 53.13

Lembrando que os ângulos α e β são suplementares, é cumprido:

α + β = 180º ⇒ β = 180 - 53.13 = 126.87º

Solução d

O comprimento do segmento RX é facilmente calculado, porque há informações suficientes para encontrá -las. Por exemplo, através de:

Rx = rv . cos α = 15 . Cos 53.13th u.para. = 9 u.para.

Também através do teorema de Pitágoras através do triângulo retângulo dos lados 15 e 12 u.para:

(RV)² = (Rx)² + h²

Limpando a duração do segmento de interesse:

Rx = √ [(rv)² - h²] = √ [15² - 12²] = √81 = 9

Solução e

A medida de uma das diagonais, por exemplo, a diagonal que se junta aos vértices R e T, que é uma grande diagonal, é dada pelo teorema de cosseno, como explicado anteriormente, por isso substituímos os valores lá:

D_M = √ (20² + 25² - 2. vinte. quinze .Cos 126.87º) = 37.22 u.para.

Para a diagonal menor:

D_m = √ (20² + 25² - 2. vinte. quinze .Cos 53.13º) = 25.79 u.para.

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Baldor, a. 1973. Geometria e trigonometria. Editorial cultural da América Central.
3. E. PARA. 2003. Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
4. Jiménez, r. 2010. Matemática II. Geometria e trigonometria. Segunda edição. Prentice Hall.
5. Polígonos regulares. Recuperado de: companheiro.Engenharia.USAC.Edu.Gt.
6. Fórmulas do Universo. Rombóide. Recuperado de: universoformulas.com.
7. Wikipedia. Rombóide. Recuperado de: é.Wikipedia.org.