Triangles História, Elementos, Classificação, Propriedades

O triângulos São figuras geométricas planas e fechadas, que consistem em três lados. Um triângulo é determinado por três linhas que são cortadas duas a duas, formando -se entre três ângulos. A forma triangular, cheia de simbolismo, está presente em inúmeros objetos e como um elemento de construção.

A origem do triângulo está perdida na história. A partir de evidências arqueológicas, sabe -se que a humanidade primitiva o conhecia bem, porque os restos arqueológicos confirmam que ele era usado em ferramentas e armas.

figura 1. Triângulos. Fonte: Public DomainParturas.

Também é evidente que os antigos egípcios tinham um sólido conhecimento de geometria e, em particular, da forma triangular. Eles estavam incorporados nos elementos arquitetônicos de suas construções monumentais.

No papiro Rhind, existem fórmulas para o cálculo de triângulos e áreas de trapezista, bem como alguns volumes e outros conceitos de trigonometria rudimentar.

Por outro lado, sabe -se que os babilônios foram capazes de calcular a área do triângulo e outras figuras geométricas, que usaram para fins práticos, como as divisões da terra. Eles também estavam cientes de muitas propriedades dos triângulos.

No entanto, foram os gregos antigos que sistematizaram muitos dos conceitos geométricos frequentes hoje, embora grande parte desse conhecimento não fosse exclusiva, pois certamente foi compartilhado com essas outras civilizações antigas.

[TOC]

Elementos do triângulo

Os elementos de qualquer triângulo são indicados na figura a seguir. Existem três: vértices, lados e ângulos.

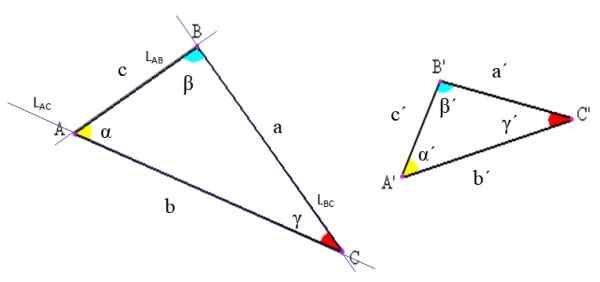Figura 2. Notação de triângulos e seus elementos. Fonte: Wikimedia Commons, modificada por F. Zapata

-Vértices: Estes são os pontos de interseção das linhas cujos segmentos determinam o triângulo. Na figura superior, por exemplo, a linha L_AC que contém o segmento CA, cruza a linha L_Ab que contém segmento ab apenas no ponto A.

-Lados: Entre cada par de vértices, é desenhado um segmento de linha que constitui um lado do triângulo. Este segmento pode ser indicado com as letras das extremidades ou usando uma carta específica para chamá -la. No exemplo da Figura 2, o lado AB também é chamado de "C".

-Ângulos: Entre cada lado com um vértice comum, um ângulo se origina, cujo vértice coincide com o do triângulo. O ângulo é geralmente indicado com uma letra grega, conforme declarado no início.

Para construir um triângulo específico, com uma determinada forma e tamanho, basta ter alguns dos seguintes conjuntos de dados:

-Os três lados, bastante óbvios no caso de um triângulo.

-Dois lados e o ângulo entre eles, e o lado restante é imediatamente desenhado.

-Dois ângulos (internos) e o lado entre eles. Por extensão, os dois lados ausentes são desenhados e o triângulo está pronto.

Notação

Geralmente na notação de triângulos, são usadas as seguintes convenções: os vértices são indicados com letras maiúsculas, os lados com pequenas letras latinas e os ângulos pelas letras gregas (veja a Figura 2).

Dessa maneira, o triângulo é nomeado de acordo com seus vértices. Por exemplo, o triângulo à esquerda na Figura 2 é o Triângulo ABC, e o da direita é o triângulo A'b'c '.

Também é possível usar outras notações; Por exemplo, o ângulo α na Figura 2 é indicado como BAC. Observe que a letra do vértice entra no meio e as letras são escritas na direção oposta às agulhas do relógio.

Pode atendê -lo: delimitação do problema

Outras vezes, um sotaque circunflexo é colocado para denotar o ângulo:

Ou o símbolo porte é usado, pois a notação anterior pode não ser fácil na impressão, seguida pela letra correspondente ao vértice:

α = ero

Tipos de triângulos

Existem vários critérios de classificação dos triângulos. O mais comum é classificá -los de acordo com a medida de seus lados ou de acordo com a medida de seus ângulos. Dependendo da medida de seus lados, os triângulos podem ser: escalenos, isósceles ou equiláteis:

-Escaleno: Seus três lados são diferentes.

-Isósceles: Tem dois lados diferentes e um.

-Equilátero: Os três lados são iguais.

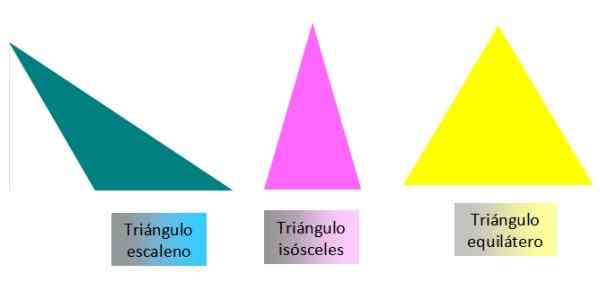Figura 3. Classificação de triângulos de lado. Fonte: f. Zapata

De acordo com a medida de seus ângulos, os triângulos são chamados assim:

-Obtuso, Se um dos ângulos internos for maior que 90º.

-Acutangle, Quando os três ângulos internos do triângulo são agudos, ou seja, menos de 90º

-Retângulo, No caso de um de seus ângulos internos valer 90º. Os lados que formam 90º são chamados Catetos e o lado oposto ao ângulo certo é a hipotenusa.

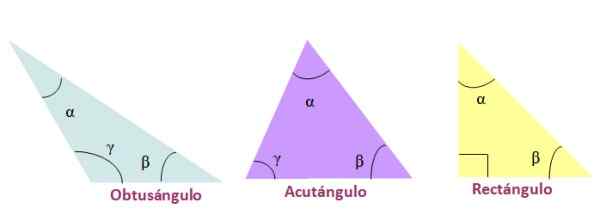Figura 4. Classificação de triângulos por seus ângulos internos. Fonte: f. Zapata.

Congruência de triângulos

Quando dois triângulos têm a mesma forma e são de tamanho igual, diz -se que eles são congruentes. É claro que a congruência está relacionada à igualdade, então por que na geometria falamos sobre "dois triângulos congruentes" em vez de "dois triângulos iguais"?

Bem, é preferido usar o termo "congruência" para manter a verdade, já que dois triângulos podem ter a mesma forma e tamanho, mas ser orientado de maneira diferente no plano (veja a Figura 3). Do ponto de vista da geometria, eles não seriam mais estritamente iguais.

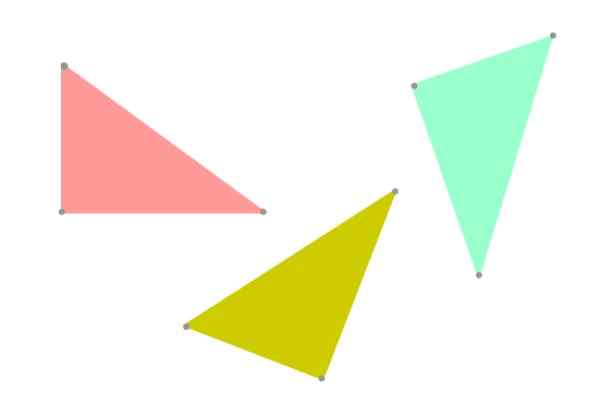Figura 5. Triângulos congruentes, mas não necessariamente os mesmos, porque sua orientação no avião é diferente. Fonte: f. Zapata.

Critérios de congruência

Dois triângulos são congruentes se ocorrer alguma das seguintes situações:

-Os três lados medem o mesmo (novamente este é o mais óbvio).

-Eles têm dois lados idênticos e com o mesmo ângulo entre eles.

-Ambos têm dois ângulos internos idênticos e o lado entre esses ângulos é o mesmo.

Como pode ser visto, trata -se dos dois triângulos atendem às condições necessárias para que, ao construí -los, sua forma e tamanho sejam exatamente iguais.

Os critérios de congruência são muito úteis, pois na prática, inúmeras peças e peças mecânicas devem ser fabricadas em série, de modo que suas medidas e forma são exatamente iguais.

Similaridade dos triângulos

Um triângulo é semelhante a outro se eles tiverem a mesma forma, mesmo que sejam de tamanho diferente. Para garantir que a forma seja a mesma, é necessário que os ângulos internos tenham o mesmo valor e que os lados sejam proporcionais.

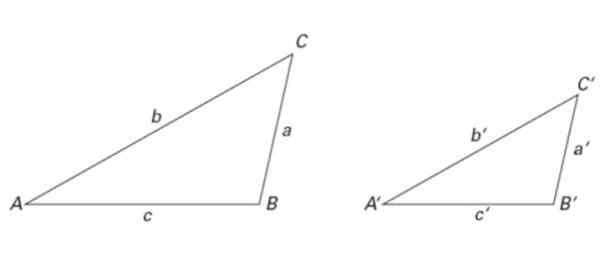Figura 6. Dois triângulos semelhantes: seus tamanhos diferem, mas suas proporções são iguais. Fonte: f. Zapata.

Os triângulos da Figura 2 também são semelhantes, bem como os da Figura 6. Desta forma:

Ero a = porte A ', ϩ B = porte B 'e ϩ C = A C '

Quanto aos lados, os seguintes motivos de similaridade são atendidos:

a/a '= b/b' = c/c '

Propriedades

As propriedades fundamentais dos triângulos são as seguintes:

-A soma dos ângulos internos de qualquer triângulo é sempre 180º.

-Para qualquer triângulo, a soma de seus ângulos externos é igual a 360 °.

Pode atendê -lo: pesquisa básica: características, definição, exemplos

- Um ângulo externo de um triângulo é igual à soma dos dois ângulos internos não adjacentes a esse ângulo.

Teoremas

Primeiro teorema de tal

Eles são atribuídos ao filósofo grego e contos matemáticos de Miletus, que desenvolveram vários teoremas relacionados à geometria. O primeiro deles estabelece o seguinte:

Se várias linhas paralelas cortam duas linhas transversais, elas determinam segmentos proporcionais.

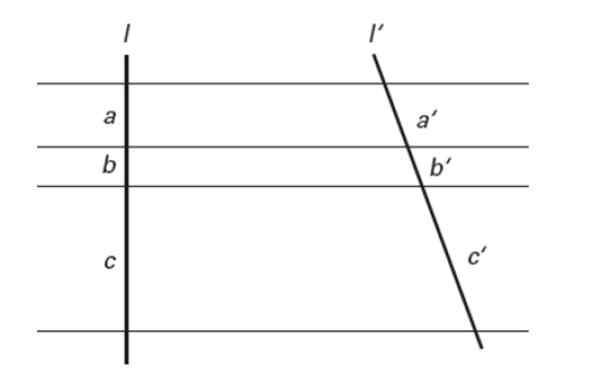Figura 7. The Tales Teorema. Fonte: f. Zapata.

Em outras palavras:

a/a '= b/b' = c/c '

O primeiro teorema de tal é aplicável a um triângulo, por exemplo, existe o triângulo azul ABC à esquerda, que é cortado pelos paralelos vermelhos à direita:

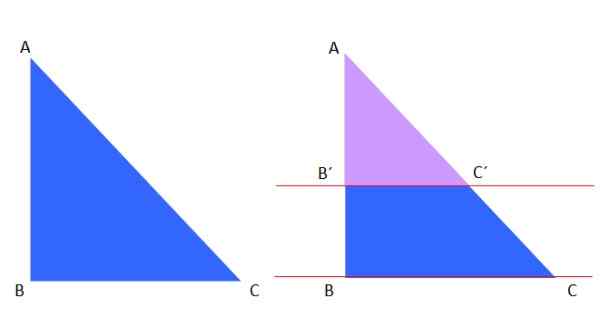Figura 8. O teorema de tal e os triângulos semelhantes.

O Triângulo Violet de Violet é semelhante ao Triângulo ABC Blue, portanto, de acordo com esse teorema, o seguinte pode ser escrito:

Ab '/ac' = ab/ac

E é consistente com o que foi explicado acima no segmento da similaridade dos triângulos. A propósito, linhas paralelas também podem ser verticais ou paralelas à hipotenusa e triângulos semelhantes são obtidos.

Segundo teorema deste

Este teorema também se refere a um triângulo e uma circunferência central ou, como os mostrados abaixo. Nesta figura, o AC é um diâmetro da circunferência e B é um ponto dela, sendo B diferente de A e B.

O segundo teorema de tais estados que:

O ângulo entre os segmentos AB e BC é sempre 90º, portanto o triângulo ABC é retângulo.

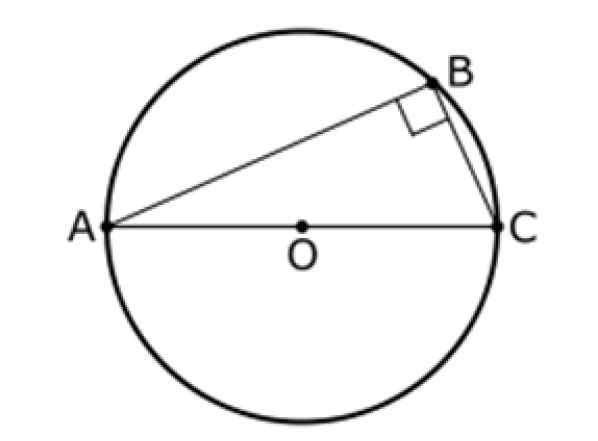Figura 9. O segundo teorema de tal. Fonte: Wikimedia Commons. InductiveLoad [domínio público].

Teorema de Pitágoras

Este é um dos teoremas mais famosos da história. É devido aos pitágoras matemáticas gregas de Samos (569 - 475 para. C.) e é aplicável a um triângulo certo. Diz assim:

A soma dos quadrados dos comprimentos que as categorias de triângulo retângulo é igual ao comprimento da hipotenusa alta ao quadrado.

Se tomarmos como exemplo o triângulo azul da Figura 8, ou o triângulo violeta, como ambos são retângulos, pode -se dizer que:

AC² = Ab² + Bc² (Triângulo Azul)

AC '² = Ab '² + BC '² (Triângulo Violet)

A área de um triângulo

A área do triângulo é dada pelo produto de sua base para e sua altura h, dividido por 2. E por trigonometria, essa altura pode ser escrita como H = b sinθ.

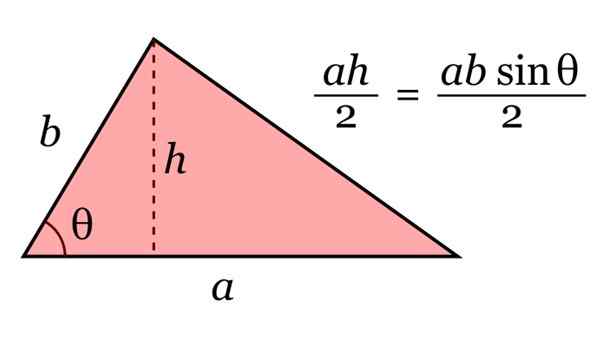Figura 10. Área do triângulo. Fonte: Wikimedia Commons.

Exemplos de triângulos

Exemplo 1

Dizem que, através de seu primeiro teorema, esse conseguiu medir a altura da Grande Pirâmide no Egito, uma das 7 maravilhas do mundo antigo, medindo a sombra que projetou no chão e a que projeta uma estaca presa em o chão.

Este é o esquema do procedimento seguido por tal:

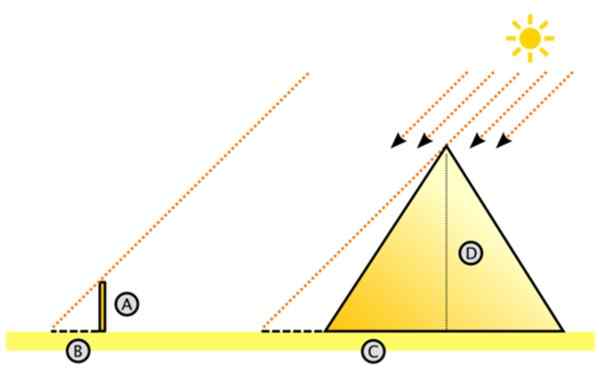Figura 11. Esquema para medir a altura da Grande Pirâmide por similaridade dos triângulos. Fonte: Wikimedia Commons. DAKE [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

Tal suposto que os raios do sol afetam paralelos. Com isso em mente, ele imaginou o grande triângulo direito.

Há a altura da pirâmide e C é a distância no chão medido do centro para a sombra projetada pela pirâmide no piso do deserto. Pode ser trabalhoso medir C, mas certamente é mais fácil do que medir a altura da pirâmide.

À esquerda está o pequeno triângulo, dos gatos A e B, onde A é a altura da estaca presa verticalmente no chão e B é a sombra que projeta. Ambos os comprimentos são mensuráveis, assim como C (C é igual ao comprimento da sombra + metade do comprimento da pirâmide).

Pode atendê -lo: o que são estímulos táteis?

Então, por similaridade dos triângulos:

A/b = d/c

E a altura da Grande Pirâmide acaba sendo: D = C.(A/b)

Exemplo 2

Armadura de construção civil são estruturas baseadas em barras retas finas ou metal, que são usadas como suporte em muitos edifícios. Eles também são conhecidos como treliças, treliças ou reticulado (Treliça em inglês).

Neles os triângulos estão sempre presentes, porque as barras estão interconectadas em pontos chamados nós, que podem ser fixos ou articulados.

Figura 12. O triângulo está presente no quadro desta ponte. Fonte: pxhere.

Exemplo 3

O método conhecido como triangulação permite obter a localização de pontos inacessíveis, sabendo outras distâncias mais fáceis de medir, com a condição que um triângulo é formado que inclua entre seus vértices o local desejado.

Por exemplo, na figura a seguir, você deseja saber em que ponto o mar é o navio, denotado como B.

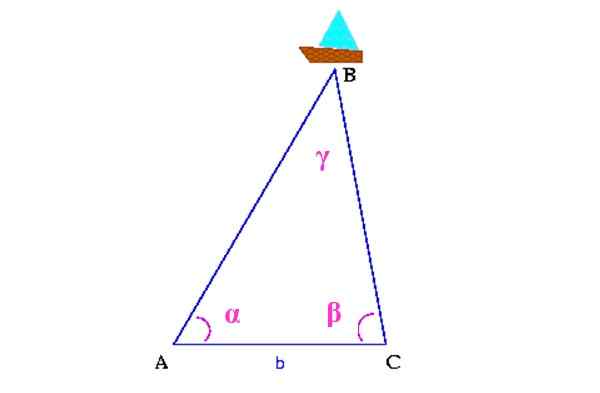Figura 13. Esquema de triangulação para localizar o navio. Fonte: Wikimedia Commons. Colette [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

Primeiro, a distância entre dois pontos na costa é medida, que na figura são A e C. Então você deve determinar os ângulos α e β, com a ajuda de um teodolito, Um dispositivo que serve para medir ângulos verticais e horizontais.

Com todas essas informações, um triângulo é construído sobre cujo vértice superior é o navio. Reduziria o ângulo γ, por meio.

Exercícios

Exercício 1

Na figura mostrada, os raios do sol são paralelos. Dessa maneira. Naquele mesmo tempo, a sombra do edifício é de 40 metros. Seguindo esse teorema de tal, encontre a altura do edifício.

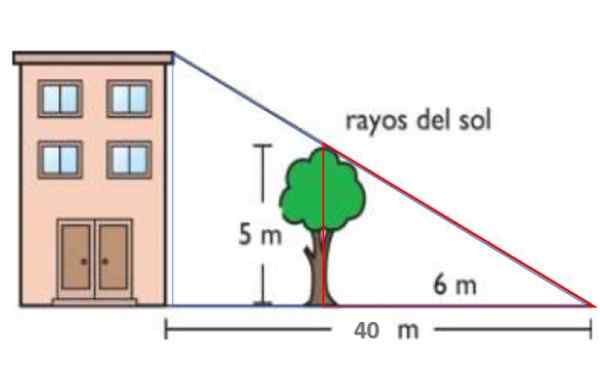Figura 14. Esquema para o ano resolvido 1. Fonte: f. Zapata.

Solução

O triângulo vermelho tem lados de 5 e 6 metros, respectivamente, enquanto o azul tem uma altura h -a altura do edifício e base 40 metros. Ambos os triângulos são semelhantes, portanto:

H / 40 = 5/6 → H = 40.(5/6) M = 33.3 m

Exercício 2

Você precisa conhecer a distância horizontal entre dois pontos PARA e B, Mas eles estão localizados em um terreno muito irregular.

Aproximadamente no ponto médio (P_m) Dessa terra, um destaque de 1 se destaca.75 metros de altura. Se a fita métrica indicar 26 metros de comprimento medidos de A para a proeminência e 27 metros de B ao mesmo ponto, encontre a distância Ab.

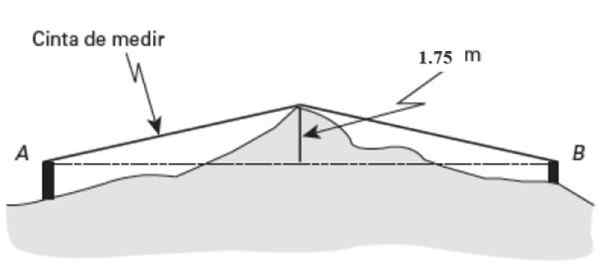Figura 15. Esquema para o exercício resolvido 2. Fonte: Jiménez, R. Matemática II. Geometria e trigonometria.

Solução

O teorema de Pitágoras é aplicado a um dos dois retângulos triângulos na figura. Começando com o da esquerda:

Hipotenuse = c = 26 metros

Altura = a = 1.75 metros

AP_m = (26² - 1.75²)^1/2 = 25.94 m

Agora, as pitágoras são aplicadas no triângulo certo, desta vez c = 27 metros, a = 1.75 metros. Com estes valores:

Bp_m= (27² - 1.75²)^1/2 = 26.94 m

A distância AB está adicionando estes resultados:

AB = 25.94 m +26.94 m = 52.88 m.

Referências

1. Baldor, J. PARA. 1973.Geometria plana e espacial. Cultural da América Central.
2. Barredo, d. A geometria do triângulo. Recuperado de: ficus.Pntic.Mec.é.
3. Jiménez, r. 2010. Matemática II. Geometria e trigonometria. Segunda edição. Pearson.
4. Wentworth, G. Geometria do Planeta. Recuperado de: Gutenberg.org.
5. Wikipedia. Triângulo. Recuperado de: é. Wikipedia.org.