Triângulo obtuso

Explicamos o que é um triângulo obtuso, seus elementos, características, tipos, exemplos e um exercício resolvido

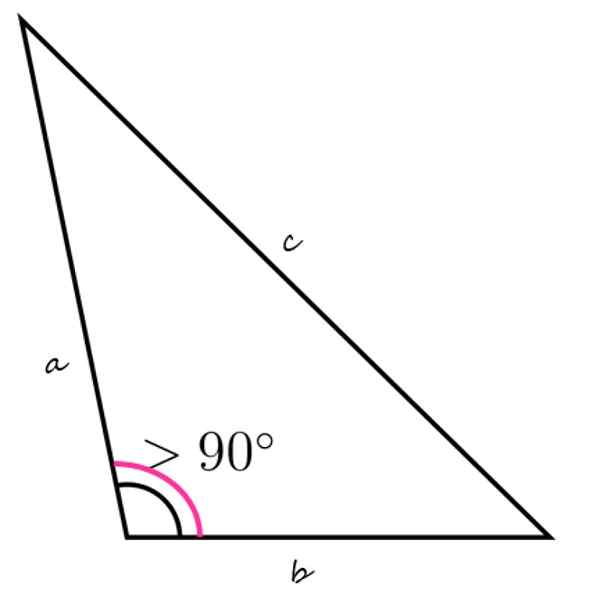O triângulo obtuso é caracterizado por ter um ângulo interno maior que 90º

O que é um triângulo obtuso?

A Triângulo obtuso É a figura plana, fechada e com três lados, que também contém um ângulo interno obtuso, isto é, maior que 90º e menor que 180º.

Qualquer triângulo contém 3 ângulos internos e, se um deles for obtuso, os outros dois são, por força, agudos, porque a soma dos ângulos internos de qualquer triângulo é sempre igual a 180º.

A figura superior mostra um exemplo de um triângulo obtuso, com o ângulo interno inferior esquerdo maior que 90º. Os ângulos internos restantes devem adicionar menos de 90º, apenas dessa maneira é verdade que a soma dos três é igual a 180º.

Além dos triângulos obtusos, existem triângulos acutangulosos, se todos os seus ângulos internos são agudos e triângulos de retângulo, quando um dos ângulos internos mede exatamente 90º.

Elementos dos triângulos obtusos

Os triângulos obtusángulos têm elementos comuns para todos os triângulos: são figuras planas de 3 anos, com 3 ângulos internos e 3 vértices. Além disso, eles têm segmentos notáveis, chamados CEVIANOS, como altura, mediana e mediantrix e pontos em que os cevanos se cruzam.

Cada um desses elementos é brevemente definido da seguinte forma:

-Lados, são os segmentos que compõem a figura.

-Vértices, Pontos de interseção de cada par de lados adjacentes.

-Ângulos internos, Eles estão entre dois lados adjacentes, no lado interno da figura, coincidindo o vértice do ângulo com o do triângulo.

-Ângulos externos, Eles estão entre um lado e a extensão do lado adjacente, fora da figura, sendo o vértice comum, tanto do triângulo quanto do ângulo. A soma da medida entre o ângulo interno e seu ângulo adjacente externo é de 180º, para que sejam ângulos complementares.

Pode atendê -lo: Teste de Tukey: O que é, em caso de exemplo, exercício resolvido

-Altura, É a medida do segmento perpendicular que se junta a um vértice com o lado oposto, ou com a extensão deste.

-Mediana, linha que é direcionada de um vértice para o centro do lado oposto.

-MediaTrix, segmento perpendicular ao lado e isso passa apenas pelo seu centro.

-Bissetor, É um segmento que divide em metade um ângulo interno do triângulo.

-Orocentro, ponto de interseção das três alturas.

-BaryCenter, Também chamado de centróide, é o ponto em que os três medianos se cruzam.

-Circunncentro, Aqui os três mediatrices são cortados.

-No centro, Ponto de confluência dos bissetores.

Depois que esses conceitos foram revisados, algumas das características mais notáveis ​​dos triângulos obtusos são descritos abaixo.

Caracteristicas

1.- A soma dos três ângulos internos do triângulo obtuso é de 180º, portanto, apenas um de seus ângulos internos pode ser maior que 90º, enquanto a soma dos dois restantes é menor que 90º.

2.- O lado mais longo do triângulo obtuso se opõe ao ângulo obtuso.

3.- Em um triângulo obtuso, as alturas dos vértices que fazem ângulo agudo, atravessam as extensões dos lados opostos.

4.- O ortocentro de um triângulo obtuso está fora da figura.

5.- O circunncentro do triângulo obtuso também cai do triângulo (isso não acontece com o triângulo Acutangle).

6.- Só é possível registrar um quadrado no triângulo obtuso, apoiando um dos lados do quadrado no lado mais longo do triângulo. Dois quadrados podem ser desenhados, apoiando o lado nos lados mais curtos do triângulo, deixando um vértice não registrado (que não toca o lado do triângulo).

Pode servir você: Tidecágono

7.- Ser um triângulo obtuso dos lados (a, b, c), sendo c o lado mais longo. A seguinte desigualdade é válida:

para²+b² < c²

8.- São dois triângulos obtusos, cujos respectivos lados são (a, b, c) e (u, v, w). Os lados mais longos de cada um são C e W, então a seguinte desigualdade é cumprida:

A ∙ U + B ∙ V < c∙w

Tipos de triângulos impedindo

Os triângulos obtusos podem ter dois tipos, de acordo com a duração de seus lados:

• Isósceles
• Escaleno

Eles são descritos brevemente abaixo:

Triângulo isósceles

É aquele que tem dois lados iguais e um diferente, ou seja, seus lados são (a, a, c).

Quando o triângulo de isosceles é obtuso, os lados da medida "A" são mais curtos e o lado "C" é o mais longo. O ângulo obtuso é formado entre os mesmos lados, enquanto os dois ângulos agudos são de igual medida e são formados entre os lados "A" e o lado "C".

E, como afirmado na seção anterior, lado "C", porque é o mais longo, é oposto ao ângulo obtuso.

Triângulo escaleno

Os três lados do triângulo scalene têm uma medida diferente: (a, b, c).

Exemplos

Exemplo 1

O triângulo mostrado na figura a seguir é obtuso. O ângulo obtuso é γ = 114.5º e é verificado que a soma dos três ângulos internos é 180º:

114.5º + 36.8º + 28.6º 180º

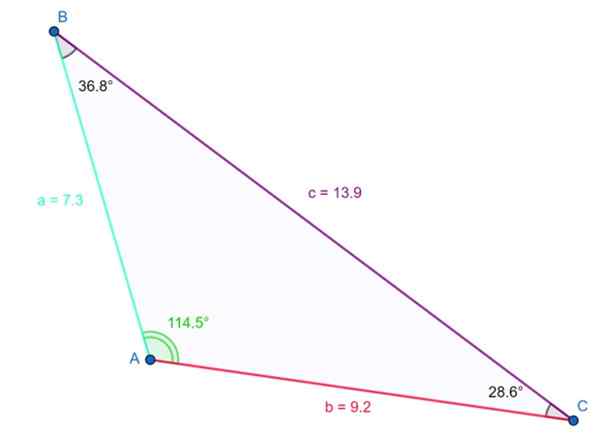Exemplo de triângulo obtuso. Fonte: f. Zapata

O lado mais longo mede 13.9 unidades e se opõe ao ângulo obtuso. A desigualdade acima mencionada também é atendida:

para²+b² < c²

Pode atendê -lo: relações de proporcionalidade: conceito, exemplos e exercícios

Sim a = 7.3 e B = 9.2, então:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Exemplo 2

No triângulo Calabi, é possível colocar o maior quadrado possível, de três maneiras diferentes dentro do triângulo, como mostrado na figura a seguir.

O triângulo de Calabi é isósceles e obtuso. O ângulo obtuso é de aproximadamente 101.736 ° e ângulos agudos na base medem ambos 39.13º, também aproximadamente.

Exercício resolvido

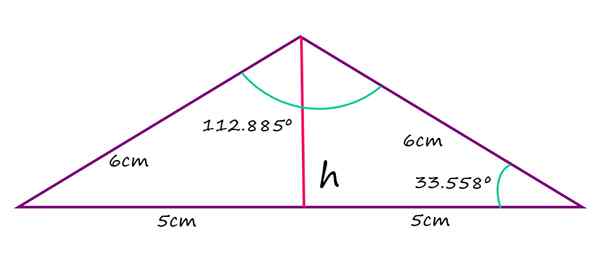
Os lados iguais de um triângulo de isósceles obtusos medem 6 cm, enquanto o lado mais longo mede 10 cm. Calcule o valor do ângulo obtus.

Solução

O teorema de cosseno pode ser usado para encontrar o cosseno do ângulo obtuso. Então, com a ajuda da calculadora, o ângulo em questão é determinado, indicado como γ.

O teorema de Coseno afirma que:

c² = a² +b² - 2ab ∙ cos γ

Onde γ é o ângulo entre os lados a e b. Como o triângulo é isósceles, os lados A e B são os mesmos, portanto:

c² = 2a² - 2º²∙ cos γ

Limpeza cos γ:

 O ângulo obtuso é o arco -0 cosseno.38889, que é aproximadamente 112.885º. O valor de α, o ângulo agudo formado pelos lados de 6 cm com os 10 cm é:

2α + 112.885º = 180º

α = (180 - 112.885)/2 = 33.558º

Triângulo obtuso de isósceles. Fonte: f. Zapata

Quanto à altura do triângulo, medido a partir da base, é obtido observando que essa altura divide o triângulo em dois retângulos iguais, com hipotenusa igual a 6 cm e base 5 cm. Nesse caso, o teorema de Pitágoras se aplica diretamente para encontrar o valor de H: