Triângulo escaleno

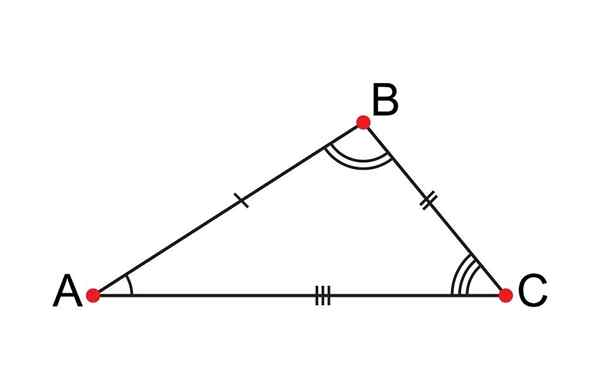O triângulo Scalene tem todos os seus lados desiguais

O que é um triângulo Scalene?

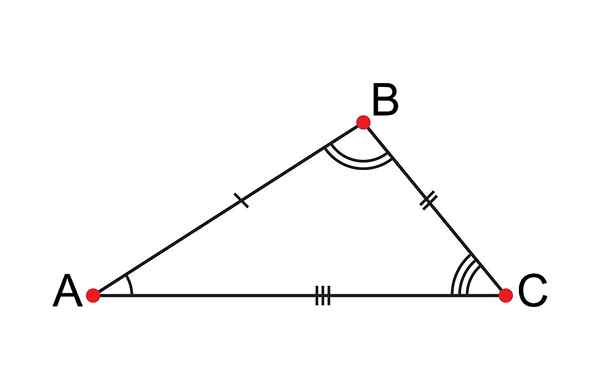
A Triângulo escaleno É um polígono de três lados, onde todos têm medidas ou comprimentos diferentes; Por esse motivo, recebeu o nome de Escaleno, que em latim significa desigual.

Os triângulos são polígonos considerados os mais simples na geometria, porque três lados, três ângulos e três vértices são formados. No caso do triângulo Scaleno, por ter todos os lados diferentes, isso implica que seus três ângulos também serão.

Características dos triângulos em escala

Os triângulos de escala são polígonos simples, porque nenhum de seus lados ou ângulos tem a mesma medida, ao contrário dos triângulos de isósceles e equilíbrio.

Como todos os seus lados e ângulos têm medidas diferentes, esses triângulos são considerados polígonos convexos irregulares.

De acordo com a amplitude dos ângulos internos, os triângulos scalene são classificados como:

• Triângulo retângulo Scaleno: Todos os seus lados são diferentes. Um de seus ângulos é reto (90^qualquer) e os outros são agudos e com medidas diferentes.
• Triângulo obtuso de Scalene: Todos os seus lados são diferentes e um de seus ângulos é obtuso (> 90^qualquer).
• Triângulo de Scalene acutangle: Todos os seus lados são diferentes. Todos os seus ângulos são agudos (< 90^qualquer), Com medidas diferentes.

Outra característica dos triângulos scalene é que devido ao inconsistente.

Componentes/elementos

A mediana

É uma linha que sai do ponto médio de um lado e chega ao vértice oposto. Os três meios participam em um ponto chamado Baricentro ou Centroid.

O bissetor

É um semi -direito que divide cada ângulo em dois ângulos de igual medida. Os bissetores de um triângulo concordam em ponto chamado Incenter.

A MediaTrix

É um segmento perpendicular ao lado do triângulo, que se origina no meio deste. Existem três mediatrices em um triângulo e participam em um ponto chamado Curcrontro.

A altura 

É a linha que vai do vértice para o lado oposto, e também essa linha é perpendicular a esse lado. Todos os triângulos têm três alturas que coincidem em um ponto chamado Ortotenter.

Propriedades do Triange Escaleno

Os triângulos de escala são definidos ou identificados porque têm várias propriedades que os representam, originados dos teoremas propostos por grandes matemáticos. Elas são:

Ângulos internos

A soma dos ângulos internos é sempre igual a 180^qualquer.

Soma dos lados

A soma das medidas de dois lados deve ser sempre maior que a medida do terceiro lado, a + b> c.

Lados incongruentes

Todos os lados dos triângulos de escalada têm medidas ou comprimentos diferentes; isto é, eles são incongruentes.

Ângulos incongruentes

Como todos os lados do triângulo scalene são diferentes, seus ângulos também serão. No entanto, a soma dos ângulos internos sempre será igual a 180º e, em alguns casos, um de seus ângulos pode ser obtuso ou reto, enquanto em outros todos os seus ângulos serão agudos.

Pode atendê -lo: problemas multiplicativos para crianças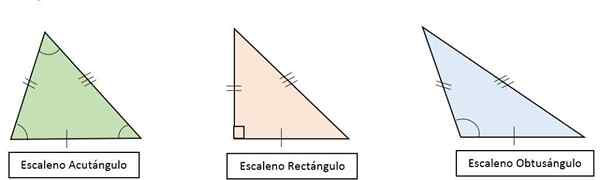 Tipos de triângulos de Scalele de acordo com seus ângulos

Altura, mediana, mediatrrix e bissetor não são coincidentes

Como qualquer triângulo, Escaleno possui várias linhas de linhas que o compõem, como: altura, média, mediatrix e bissetor.

Devido à particularidade de seus lados, neste tipo de triângulo, nenhuma dessas linhas coincidirá em um único.

Orocentro, Baricentro, Incentro e Circuncentro não são coincidentes

Como a altura, mediana, bissetor e mediatrix são representados por diferentes segmentos de linha, em um triângulo escaleno os pontos de encontro -o ortocentro, o incentivo e o baricentercenter -serão encontrados em diferentes pontos (ou seja, eles não coincidem).

Dependendo se o triângulo é acutangle, retângulo ou obtuso, o ortocentro possui locais diferentes:

para. Se o triângulo for acutangle, o ortocentro estará dentro do triângulo.

b. Se o triângulo for retângulo, o ortocentro coincidirá com o vértice no lado reto.

c. Se o triângulo for obtuso, o ootocenter estará fora do triângulo.

Alturas relativas

As alturas são relativas aos lados.

No caso do triângulo Scaleno, essas alturas terão medidas diferentes. Todo triângulo tem três alturas relativas e para calculá -los, a fórmula de Herón é usada.

Cálculo do perímetro, área, altura e lados

Como calcular o perímetro?

O perímetro de um polígono é calculado pela soma dos lados.

Como neste caso o triângulo Scalene tem todos os seus lados com uma medida diferente, seu perímetro será:

P = lado para + lado b + lado c.

Como calcular a área?

Os triângulos são sempre calculados com a mesma fórmula, multiplicando a base por altura e dividindo por dois:

Área = (base _* H) ÷ 2

Em alguns casos, a altura do triângulo Scaleno não é conhecida, mas há uma fórmula proposta pelo matemático Herón, para calcular a área sabendo a medida dos três lados de um triângulo.

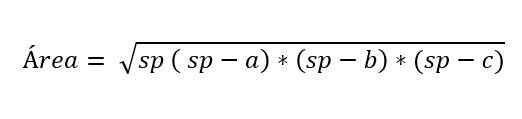
Onde:

• A, B e C representam os lados do triângulo.
• O SP corresponde ao semi -perímetro do triângulo, ou seja, metade do perímetro:

sp = (a + b + c) ÷ 2

No caso de apenas dois lados do triângulo e o ângulo formado entre eles, a área pode ser calculada aplicando as razões trigonométricas. Assim você tem que:

Área = (lado _* H) ÷ 2

Onde a altura (h) é o produto de um lado através do ângulo oposto. Por exemplo, para cada lado, a área será:

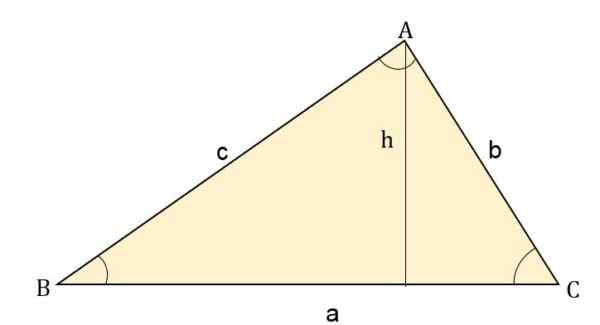
• Área = (b _* c _* pecado a) ÷ 2
• Área = (a _* c _* pecado b) ÷ 2.
• Área = (a _* b _* Sen c) ÷ 2

Como calcular a altura?

Como todos os lados do triângulo Scalene, eles são diferentes, não é possível calcular a altura com o teorema de Pitágoras.

Da fórmula de Herón, que se baseia nas medidas dos três lados de um triângulo, a área pode ser calculada.

Pode atendê -lo: notação fatorial: conceito, exemplos e exercícios

A altura pode ser clara da fórmula geral da área:

Fórmula para calcular a altura de um triângulo escaleno

O lado é substituído pela medida do lado a, b ou c.

Outra maneira de calcular a altura quando o valor de um dos ângulos é conhecido, é aplicar os motivos trigonométricos, onde a altura representará um triângulo Cateto.

Por exemplo, quando o ângulo oposto é conhecido por altura, será determinado pela mama:

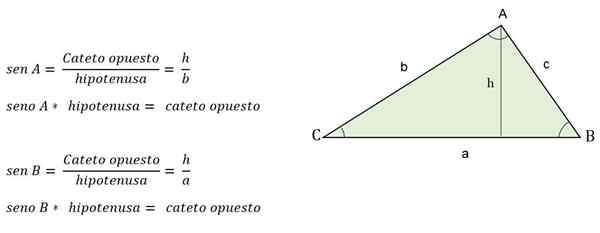Fórmula trigonométrica para calcular a altura de um triângulo escaleno

Como calcular os lados?

Quando você tem a medida de dois lados e o ângulo oposto a eles, é possível determinar o terceiro lado aplicando o teorema de Cosenos.

Por exemplo, em um triângulo AB, a altura em relação ao segmento CA é desenhada. Dessa maneira, o triângulo é dividido em dois triângulos de retângulo.

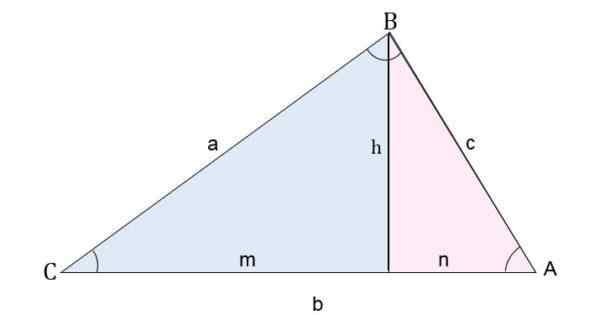Divisão de um triângulo Scalene em dois retângulos para calcular os lados

Para calcular o lado C (segmento AB), o teorema de Pitágoras para cada triângulo é aplicado:

• Para o triângulo azul que você precisa:

c² = h² + m²

Como m = b - n, é substituído:

c² = h² + b² (B - n)²

c² = h² + b² - 2bn + N².

• Para o triângulo rosa, você precisa:

h² = a² - n²

É substituído na equação anterior:

c² = a² - n² + b² - 2bn + N²

c² = a² + b² - 2bn.

Sabendo que n = a _* Cos C, é substituído na equação anterior e o valor do lado C é obtido:

c² = a² + b² - 2b_* para _* cos c.

Pela lei de Cosenos, os lados podem ser calculados como:

• para² = b² + c² - 2b_* c _* coisa.
• b² = a² + c² - 2º_* c _* cos b.
• c² = a² + b² - 2b_* para _* cos c.

Há casos em que as medidas dos lados do triângulo não são conhecidas, mas sua altura e os ângulos formados nos vértices. Para determinar a área nesses casos, é necessário aplicar motivos trigonométricos.

Conhecendo o ângulo de um de seus vértices, a categoria é identificada e a razão trigonométrica correspondente é usada:

Fórmula trigonométrica para calcular os lados de um triângulo Scalene

Por exemplo, o Cateto AB será oposto para o ângulo C, mas adjacente ao ângulo a. Dependendo da lateral ou perna correspondente à altura, o outro lado é limpo para obter o valor disso.

Exercícios resolvidos

Primeiro exercício

Calcule a área e uma altura do triângulo Escalano ABC, sabendo que seus lados estão:

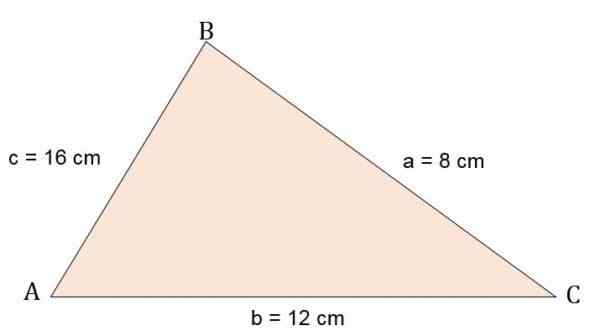
A = 8 cm.

B = 12 cm.

C = 16 cm.

Solução

Como os dados recebem as medidas dos três lados do triângulo Scalene.

Como você não tem o valor da altura, a área pode ser determinada aplicando a fórmula de Herón.

Primeiro, o semi -perímetro é calculado:

sp = (a + b + c) ÷ 2

sp = (8 cm + 12 cm + 16 cm) ÷ 2

SP = 36 cm ÷ 2

SP = 18 cm.

Agora, os valores na fórmula de Herón são substituídos:

Pode servir a você: Frequência absoluta: fórmula, cálculo, distribuição, exemplo Fórmula Herón

Conhecer a área pode ser calculada a altura relativa ao lado B. Da fórmula geral, limpando -a:

Área = (lado _* H) ÷ 2

46, 47 cm² = (12 cm _* H) ÷ 2

H = (2 _* 46,47 cm²) ÷ 12 cm

H = 92,94 cm² ÷ 12 cm

H = 7,75 cm.

Segundo exercício

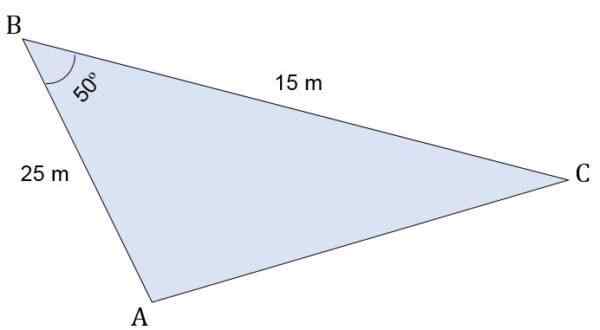
Dado o Triângulo ABC Escalano, cujas medidas são:

• Segmento AB = 25 m.
• Segmento bc = 15 m.

No vértice B, um ângulo de 50º é formado. Calcule a altura em relação ao lado C, perímetro e área desse triângulo.

Solução

Nesse caso, existem medidas de duas margens. Para determinar a altura, é necessário calcular a medida do terceiro lado.

Como o ângulo oposto é dado aos lados especificados, é possível aplicar a lei de Cosenos para determinar a medida do lado CA (b):

b² = a² + c² - 2º_*c _* cos b

Onde:

A = BC = 15 m.

C = AB = 25 m.

B = ac.

B = 50^qualquer.

Os dados são substituídos:

b² = (15)² + (25)² - 2_*(quinze)_*(25) _* cos 50

b² = (225) + (625) - (750) _* 0,6427

b² = (225) + (625) - (482.025)

b² = 367.985

B = √367.985

B = 19,18 m.

Como você já tem o valor dos três lados, o perímetro desse triângulo é calculado:

P = lado para + lado b + lado c

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Agora é possível determinar a área aplicando a fórmula Herón, mas primeiro o semi -perímetro deve ser calculado:

sp = p ÷ 2

SP = 59,18 m ÷ 2

SP = 29,59 m.

As medidas dos lados e o semi -perímetro na fórmula de Herón são substituídos:

Finalmente, conhecendo a área, a altura relativa pode ser calculada para o lado C. Da fórmula geral, limpando -a, você precisa:

Área = (lado _* H) ÷ 2

143,63 m² = (25 m _* H) ÷ 2

H = (2 _* 143,63 m²) ÷ 25 m

H = 287,3 m² ÷ 25 m

H = 11,5 m.

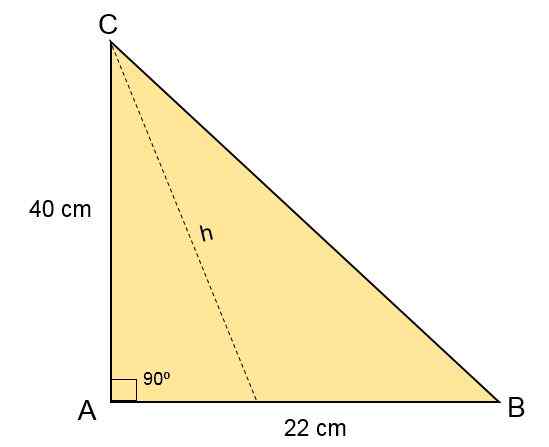
Terceiro exercício

No triângulo Escaleno ABC, o lado B mede 40 cm, o lado C mede 22 cm e no vértice A é um ângulo de 90^qualquer. Calcule a área desse triângulo.

Solução

Nesse caso, são dadas as medidas de dois lados do triângulo da escala ABC, bem como o ângulo formado no vértice para.

Para determinar a área, não é necessário calcular a medida do lado a, pois, através dos motivos trigonométricos, o ângulo é usado para encontrá -lo.

Como o ângulo oposto é conhecido pela altura, isso será determinado pelo produto de um lado e o peito do ângulo.

Substituindo na fórmula da área que você precisa:

• Área = (lado _* H) ÷ 2
• H = c _* pecado a

Área = (b _* c _* pecado a) ÷ 2

Área = (40 cm _* 22 cm _* Sen 90) ÷ 2

Área = (40 cm _* 22 cm _* 1) ÷ 2

Área = 880 cm² ÷ 2

Área = 440 cm².

Referências

1. Álvaro Rendón, para. R. (2004). Desenho técnico: caderno de atividade.
2. Ángel Ruiz, H. B. (2006). Geometrias. Cr Technological, .
3. Anjo, a. R. (2007). Álgebra Elementar. Pearson Education,.
4. Baldor, a. (1941). Álgebra. Havana: Cultura.
5. Barbosa, J. eu. (2006). Geometria euclidiana plana. Rio de Janeiro,.
6. Coxeter, h. (1971). Fundamentos da geometria. México: Limusa-wiley.
7. Daniel c. Alexander, g. M. (2014). Geometria elementar para estudantes universitários. Cengage Learning.
8. Harpe, p. d. (2000). Tópicos na teoria do grupo geométrico. University of Chicago Press.