Tidecágono

figura 1.- À esquerda, um tridecácone regular e à direita uma moeda de 20 coroas da República Tcheca, com um contorno em forma de Bridecagon inscrito em uma circunferência, por um lado, tem o leão da Bohemia e o outro para San Wenceslao, Patrono da República Tcheca, montada a cavalo. Fonte: f. Zapata.

O que é um tridecágono?

TrideCagon é uma figura geométrica plana da família Polgons e que são caracterizados por ter 13 lados e 13 vértices. Outro nome para este polígono é Triskaidecágono, Número derivado de grego.

Os 13 lados são segmentos de linha que finalmente próximos para moldar a figura. Os polígonos, que são nomeados de acordo com a quantidade de lados, são uma rica fonte de inspiração para a arquitetura, construção e design de vários objetos, tanto arte quanto utilitários.

Propriedades de Tridecágono

O Tridecágono compartilha com os outros polígonos as seguintes características e propriedades:

-Lados, Eles são os segmentos de linha que se uniram para formar a figura, que no caso do tridecágono são 13. Eles são identificados por letras minúsculas.

-Vértices, É assim que os pontos de interseção dos lados consecutivos são chamados e geralmente denotam com letras maiúsculas. O Tridecágono tem 13 vértices.

-Perímetro, equivalente à soma dos lados. Se todos os lados tiverem medida igual "A", o perímetro será simplesmente 13 × A, mas se os lados forem desiguais, o perímetro estará adicionando cada um dos comprimentos dos lados.

-Centro, É o ponto que mantém a mesma distância com os vértices e os lados.

-Diagonal, Uma linha que se junta a um vértice a outro vértice não consecutivo (os vértices consecutivos são unidos pelos lados).

-Ângulos internos, Eles são formados entre dois lados adjacentes da figura e na parte interna do polígono, e seu vértice é o vértice comum para os dois lados.

Pode atendê -lo: Miletus como o teorema

-Ângulos externos, Eles estão fora do polígono, entre um lado e o prolongamento de um dos lados consecutivos do primeiro.

-Rádio, Distância-Avertix do Tridecágon.

-Ângulo central, É aquele cujo vértice é o centro do polígono.

-Apótema, segmento que se junta ao centro de um lado com o centro da figura e forma 90º com esse lado.

Trovão regular e irregular

Três de três lugares podem ser:

-Regular, Quando a medida de todos os seus treze lados é a mesma e seus ângulos internos medem iguais.

-Irregular, Se um ou mais dos lados tiverem medidas diferentes.

No caso do Tridecácão regular, as seguintes fórmulas podem ser aplicadas:

Ângulo interno

Para um polígono regular, a fórmula que permite calcular o valor do ângulo interno é:

Onde n representa o número de lados, que neste caso é 13. Com este valor é:

I = (11 × 180º)/13 ≈ 152.3º

Diagonais

O número de diagonais é calculado pela seguinte fórmula, mesmo válida se o polígono for irregular:

Para n = 13 resultados:

D = 13 × 10/2 = 65 diagonais

Apótema

O valor de apothem l_PARA  É calculado com a seguinte fórmula, sendo "a" o comprimento do lado:

eu_PARA ≅ 2.0286a

Área

Se o perímetro P e o comprimento do apothem l_PARA, A área de Tridecágono é calculada por:

A = (p × l_PARA)/2

Dependendo do lado "A", a fórmula permanece:

A = (13a × l_PARA)/2

Substituindo a medida_PARA A partir da seção anterior, é obtida uma fórmula para a área que depende apenas do comprimento do lado:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Pode servir a você: distribuição hipergeométrica: fórmulas, equações, modelo

Exercício

Se o diâmetro de uma coroa de 20 mm for de 26 mm, quanto é o lado e a área do tridecágono registrados no círculo da moeda?

Solução

A partir da figura, existe um triângulo retângulo, cujas categorias são o apotem e metade do comprimento do lado, com o hipotenusa igual ao raio da moeda, que é metade do diâmetro. Como isso vale 26 mm, a Rádio R é igual a 13 mm.

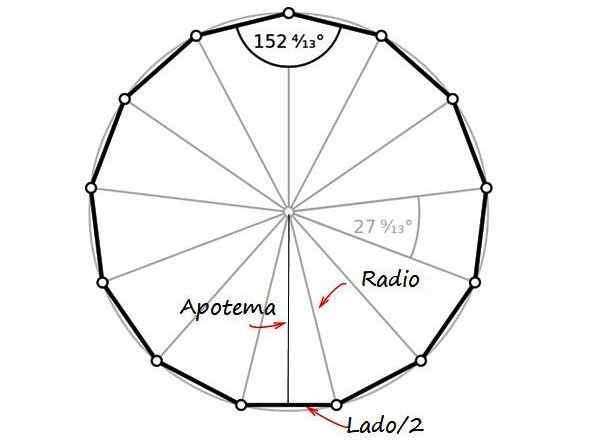Figura 2. O rádio, o apoteme e metade da lateral do trindecagon, formam um triângulo retângulo. Fonte: Wikimedia Commons/F. Zapata.

Por teorema de Pitágoras:

Desde l_PARA ≈ 2.0286a, você tem:

R² = (2.0286a)² + (0.5 ª)² = 4.3652a²

O lado é:

Com este valor, a área da moeda é:

A ≈ 13.186a² = 13.186 (6.222mm)² = 510.5 mm²

O leitor é deixado para comparar esse resultado com a área obtida assumindo que a moeda é circular do raio r = 13 mm.

Como é um tridecágono?

O TrindeCagon regular é dos polígonos que não admitem a construção exata usando apenas regra e bússola, ou seja, não é um polígono construtável. Eles são apenas edificáveis, pelo menos em teoria, aqueles polígonos cujo número de lados inclui apenas fatores primos do formulário:

Os números primos dessa maneira são chamados Primos de Fermat, Mas o número 13, embora seja primo, não tem esse formulário.

No entanto, você pode desenhar um trindecagon regular que está registrado em uma circunferência, cada vértice tem interseção com ele, sem ser notado a olho nu. Para isso, é necessário.

Pode atendê -lo: Obtusangle Triangle

Uma maneira de construir um tridecácão regular, embora não seja o único, é desenhar os golpes, como mostrado na seguinte animação:

Figura 3. Construção de um tridecagon regular. Fonte: Wikimedia Commons.

E essa outra animação também descreve como fazer um tridecágono aproximadamente, com regra e bússola:

Figura 4.- Maneira alternativa de construir um tridecagon aproximadamente regular com regra e bússola. Fonte: Wikimedia Commons.

Exemplos de Tridecágel

Thunder côncavo e convexo

Quando os ângulos internos do tridecágono são inferiores a 180º, a figura é convexa, enquanto se um ou mais ângulos internos forem maiores que 180º, então o tridecágono é côncavo.

O tridecácon regular é convexo, uma vez que seus ângulos internos medem aproximadamente 152.3º cada.

Uso de Tridecágono em numismático

Coroa tcheco

Numismática é a ciência de moedas, medalhas, ingressos e chips. Os polígonos de muitos lados são ideais como elementos decorativos no design de moedas, especialmente aqueles que têm muitos lados, como o tridecágono.

Nem todas as moedas são redondas, no entanto, os polígonos em muitos lados se assemelham à forma circular, mais lados ele tem, maior a abordagem. Portanto, os designers de moedas usam os polígonos em muitos lados para introduzir um toque de originalidade em seu design.

Vários polígonos são usados ​​com esse objetivo, como a moeda superior, chamada Coroa e da República Tcheca, um bom exemplo do uso de Tridecágono como um elemento de design.

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Desenho. Polígonos regulares. Recuperado de: desenho.com.
3. Hartley, m. Construindo um tridecágono. Recuperado de: youtube.com
4. Wikipedia. Polígono Buildível. Recuperado de: é.Wikipedia.org.
5. Wikiwand. TideCagon. Recuperado de: wikiwand.com.