Propriedades, fórmulas e equações de Escaleno Trapezio

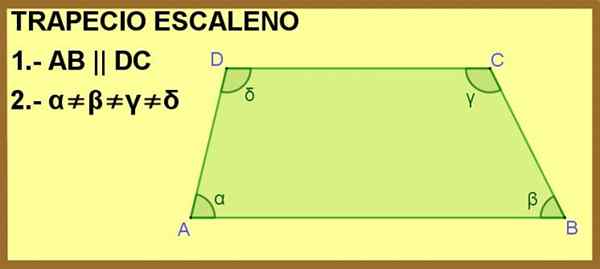
A trapézio escaleno É um polígono de quatro lados, dois dos quais são paralelos entre si e com seus quatro ângulos internos de diferentes medidas.

O quadrilateral ABCD é mostrado, onde os lados AB e DC são paralelos. Com isso, basta torná -lo um trapézio, mas, além disso, os ângulos internos α, β, γ e Δ são todos diferentes, portanto o trapézio é escalano.

figura 1. O quadrilateral ABCD é um trapézio para a condição 1 e scaleno para a condição 2. Fonte: f. Zapata.

[TOC]

Elementos do Scaleno Trapect

Abaixo dos elementos mais característicos:

-Bases e lado: Os lados paralelos do trapézio são suas bases e os dois lados não paralelos são os lados.

Em um trapezio scalene, as bases são de comprimentos diferentes e os lados também. No entanto, um trapézico scaleno pode ter um lado de igual tempo como uma base.

-Mediana: É o segmento que se junta aos pontos médios dos lados.

-Diagonal: A diagonal de um trapézio é o segmento que se junta a dois vértices opostos. Um trapézio, como todo quadrilateral, tem duas diagonais. No Scalene Trapezio, eles têm um comprimento diferente.

Outros trapézios

Além do Escaleno Trapezio, existem outros trapézios em particular: o trapézio retangular e o trapézóide de isósceles.

Um trapézio é retângulo quando um de seus ângulos é reto, enquanto trapezio isosceles tem seus lados de igual comprimento.

A forma trapezoidal possui inúmeras aplicações no nível do design e da indústria, como na configuração das asas de avião, a forma de objetos cotidianos, como mesas, backups de cadeiras, recipientes, carteiras, impressões têxteis e mais.

Figura 2. A forma trapezoidal é comum na configuração da aeronave alar. Fonte: Wikimedia Commons.

Propriedades

Em seguida, as propriedades do trapézio de escalada estão listadas, muitas das quais são extensas aos outros tipos de trapézio. A seguir, quando você fala sobre "Trapezio", a propriedade será aplicável a qualquer tipo, incluindo o Scalene.

1. A mediana do trapézio, ou seja, o segmento que une os pontos médios de seus lados não paralelos, é paralelo a qualquer uma das bases.

2.- A mediana de um trapézio tem um comprimento que é o semi -soum de suas bases e corta suas diagonais no ponto médio.

3.- As diagonais de um trapézio se cruzam em um ponto que os divide em duas seções proporcionais à proporção das bases.

4.- A soma dos quadrados das diagonais de um trapézio é igual à soma dos quadrados de seus lados, além do produto duplo de suas bases.

5.- O segmento que se junta aos pontos médios -diagonais tem comprimento igual à semi -referência das bases.

Pode atendê -lo: função injetiva: o que é consiste, para que é e exemplos

6.- Os ângulos adjacentes aos lados são suplementares.

7.- Em um trapézio escaleno, o comprimento de suas diagonais é diferente.

8.- Um trapézio tem uma circunferência registrada apenas se a soma de suas bases for igual à soma de seus lados.

9.- Se um trapézio tiver uma circunferência registrada, o ângulo com vértice no centro da referida circunferência e lados que passam pelas extremidades da lateral do trapézio é reta.

10.- Um trapézio Escaleno não tem circunferência circunscrita, o único tipo de trapézio que, se o for, é o isósceles.

Fórmulas e equações

As seguintes relações do trapézio de escalada são referidas para a figura a seguir.

1.- Se AE = Ed e BF = FC → EF || AB e EF || DC.

2.- Ef = (ab + dc)/2, ou seja: m = (a + c)/2.

3.- Di = ib = D₁ /2 e ag = gc = D₂ /2.

4.- Dj / jb = (c / a) da mesma forma CJ / JA = (c / a).

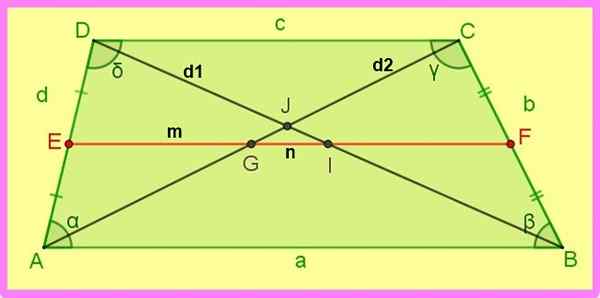Figura 3. Mediana e diagonais de um trapézico scaleno. Fonte: f. Zapata.

5.- DB² + AC² = Ad² + Bc² + 2 ab ∙ dc 

Equivalentemente:

d₁² + d₂² = d² + b² + 2 a ∙ c

6.- Gi = (ab - dc)/2

Quer dizer:

n = (a - c)/2

7.- α + δ = 180⁰ e β + γ = 180⁰

8.- Se α ≠ β ≠ γ ≠ δ então d1 ≠ d2.

9.- A Figura 4 mostra um trapézio escaleno que possui uma circunferência registrada; nesse caso, é cumprido que:

A + C = D + B

10.- Em um trapézio de escaleno ABCD com um centro registrado do centro ou o seguinte também é cumprido:

∡AOD = ∡BOC = 90⁰

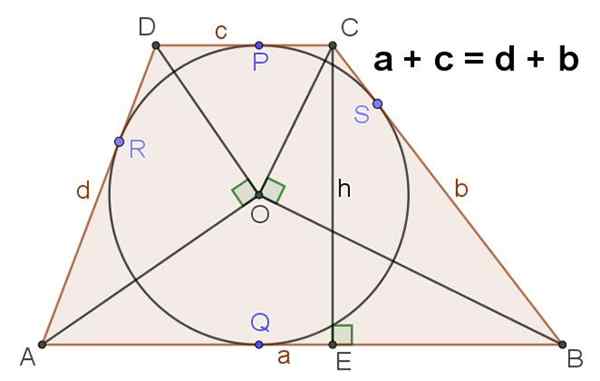Figura 4. Se em um trapézio é verificado que a soma de suas bases é igual à soma dos lados, então há a circunferência inscrita na mesma. Fonte: f. Zapata.

Altura

A altura de um trapézio é definida como o segmento que vai de um ponto da base perpendicularmente à base oposta (ou sua extensão).

Todas as alturas do trapézio têm a mesma medida H; portanto, na maioria das vezes a palavra altura refere -se à sua medição. Em resumo, a altura é a distância ou separação entre as bases.

A altura H pode ser determinada se o comprimento de um lado e um dos ângulos adjacentes ao lado é conhecido:

H = d sin (α) = d sin (γ) = b sin (β) = b sin (δ)

Mediana

A medida mediana M do trapézio são os corpos semi -Bases:

M = (a + b)/2

Diagonais

d₁ = √ [a² + d² - 2 ∙ a ∙ d ∙ cos (α)]

d₂= √ [a² + b² - 2 ∙ a ∙ b ∙ cos (β)]

Também pode ser calculado se apenas o comprimento do trapézio for conhecido:

d₁ = √ [b² + A ∙ c - a (b² - d²)/(a - c)]

d₂ = √ [d² + A ∙ C - A (D² - b²)/(a - c)]

Perímetro

O perímetro é o comprimento total do contorno, ou seja, a soma de todos os seus lados:

Pode atendê -lo: variável aleatória discreta

P = A + B + C + D

Área

A área de um trapézio são os corpos de suas bases multiplicados por sua altura:

A = h ∙ (a + b)/2

Também pode ser calculado se a altura mediana e a altura for conhecida:

A = m ∙ h

Caso apenas o comprimento dos lados do trapézio seja conhecido, a área pode ser determinada pela fórmula de Herón para o trapézio:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]

Onde s é o semi -perímetro: s = (a+b+c+d)/2.

Outros relacionamentos para a escalada de escalada

O corte da mediana com as diagonais e o paralelo que passa pela interseção das diagonais dá origem a outros relacionamentos.

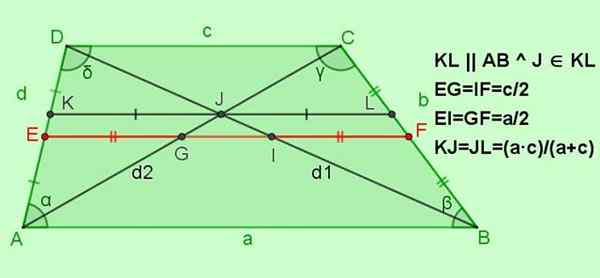Figura 5. Outros relacionamentos para a escalada de escalada. Fonte: f. Zapata.

-Relacionamentos para EF mediana

Ef = (a+c)/2; Por exemplo = if = c/2; Ei = gf = a/2

-Relações para o segmento paralelo com as bases de KL, e isso passa pelo ponto de Interseção j das diagonais

Sim kl || Ab || Dc com j ∈ Kl, então kj = jl = (a ∙ c)/(a+c)

Construção do Scalene Trapezium com regra e bússola

Dadas as bases de comprimentos para e c, sendo um> c e com o lado dos comprimentos b e d, ser b> d, Continuamos seguindo estas etapas (veja a Figura 6):

1.- Com a regra, o segmento do maior AB é desenhado.

2.- De um SE e em AB, o ponto P é marcado para que AP = C.

3.- Com a bússola com C e Radio D Center, um arco é desenhado.

4.- É feito centro em B com a Radio B desenhando um arco que interpreta o arco desenhado na etapa anterior. Chamamos isso de ponto de interseção.

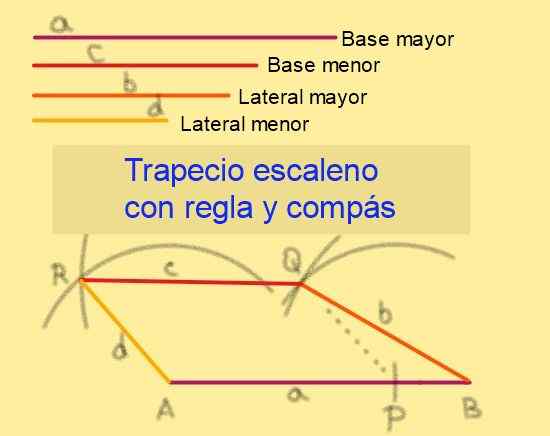Figura 6. Construção de Escaleno Trapeco dado seus lados. Fonte: f. Zapata.

5.- Com centro em desenhar um raio arco d.

6.- Com o centro para desenhar um arco de raio que interceptou para o arco desenhado na etapa anterior. Será chamado de R para o ponto de corte.

7.- Os segmentos BQ, QR e RA são desenhados com a regra.

8.- O quadrilateral ABQR é um trapézio de Scaleno, pois o APQR é um paralelogramo, o que garante que AB || Qr.

Exemplo

Os seguintes comprimentos são apresentados em CM: 7, 3, 4 e 6.

a) Determine se com eles você pode construir um trapézio escaleno que possa circunscrever para uma circunferência.

b) Encontre o perímetro, a área, o comprimento das diagonais e a altura do referido trapézio, bem como o raio da circunferência registrada.

- Solução para

Usando os segmentos do comprimento 7 e 3 como bases e os do comprimento 4 e 6 como lados, um trapezoidal scaleno pode ser construído usando o procedimento descrito na seção anterior.

Precisamos verificar se ele tem uma circunferência registrada, mas lembrando a propriedade (9):

Pode atendê -lo: prisma hexagonal

Um trapézio tem uma circunferência registrada apenas se a soma de suas bases for igual à soma de seus lados.

Vemos isso de fato:

7 + 3 = 4 + 6 = 10

Então a condição da circunferência inscrita é atendida.

- Solução b

Perímetro

O perímetro P é obtido adicionando os lados. Como as bases totalizam 10 e as laterais também, o perímetro é:

P = 20 cm

Área

Para determinar a área, conhecida apenas seus lados, o relacionamento é aplicado:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]

Onde s é o semi -perímetro:

S = (a+b+c+d)/2.

No nosso caso, o semi -perímetro vale S = 10 cm. Depois de substituir os respectivos valores:

A = 7 cm; b = 6 cm; C = 3 cm; D = 4 cm

É sobrou:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Altura

A altura h está relacionada à área A através da seguinte expressão:

A = (a+c) ∙ h/2, onde a altura pode ser obtida por liberação:

H = 2a / (a+c) = 2 * 19,84 / 10 = 3.968 cm.

Rádio de circunferência registrada

O raio da circunferência registrada vale metade da altura:

R = h/2 = 1.984 cm

Diagonais

Finalmente, há a duração das diagonais:

d₁ = √ [b² + A ∙ c - a (b² - d²)/(a - c)]

d₂ = √ [d² + A ∙ C - A (D² - b²)/(a - c)]

A substituição adequada dos valores são:

d₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

d₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

Isto é: D₁ = 4,69 cm e D₂ = 8,49 cm

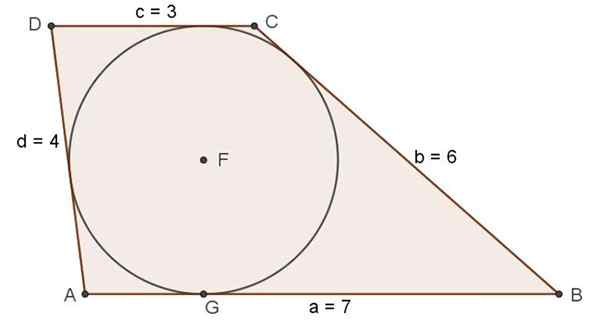Figura 7. Scalene Trapezio que atende à condição de existência de circunferência registrada. Fonte: f. Zapata.

Exercício resolvido

Determine os ângulos internos do trapézio base AB = a = 7, CD = C = 3 e BC lateral = B = 6, da = d = 4.

Solução

O teorema de cosseno pode ser aplicado para determinar os ângulos. Por exemplo, o ângulo porte = α é determinado a partir do triângulo Abd com AB = a = 7, Bd = D2 = 8,49 e DA = D = 4.

O teorema de cosseno aplicado a este triângulo permanece assim:

d₂² = a² + d² - 2 ∙ a ∙ d ∙ cos (α), ou seja:

72 = 49+16-56 ∙ cos (α).

Ao limpar, o cosseno do ângulo α é obtido:

Cos (α) = -1/8

Ou seja, α = arcCos (-1/8) = 97,18⁰.

Da mesma forma, os outros ângulos são obtidos, sendo seus valores:

β = 41,41⁰; γ = 138,59⁰ e finalmente δ = 82,82⁰.

Referências

1. C. E. PARA. (2003). Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
2. Campos, f., CERECEDO, f. J. (2014). Matemática 2. Grupo editorial da Patria.
3. Libertado, k. (2007). Descubra polígonos. Companhia de Educação de Benchmark.
4. Hendrik, v. (2013). Polígonos generalizados. Birkhäuser.
5. Iger. (s.F.). Matemática Primeiro Semestre Tacaná. Iger.
6. Jr. Geometria. (2014). Polígonos. Lulu Press, Inc.
7. Miller, Heeren e Hornsby. (2006). Matemática: Raciocínio e Aplicações (Décima Edição). Pearson Education.
8. Patiño, m. (2006). Matemática 5. Editorial Progreso.
9. Wikipedia. Trapézio. Recuperado de: é.Wikipedia.com